Paradojas de la geometría
En un número anterior nos adentramos en el mundo de las paradojas de la mano de la probabilidad. Aquí presentamos una colección de paradojas que puede sorprender. No hemos utilizado aquí la palabra sorprendente. A pesar de que las paradojas son sorprendentes en sí mismas, esta sorprendencia se sitúa normalmente en los razonamientos, pero en esta colección que traemos podemos encontrarla no sólo en los razonamientos, sino también en la vista. Esta colección podría denominarse paradoja geométrica, ya que las pruebas de los enunciados propuestos se basan tanto en conceptos geométricos como en imágenes. De momento dejaremos la clave de las paradojas en manos de los lectores, dejando las resoluciones para otro número. (Si el lector lo desea, puede enviarnos sus propias resoluciones).
Comencemos el planteamiento de paradojas.
Paradoja 1
Respecto a una recta, se pueden trazar dos líneas perpendiculares a un punto exterior.
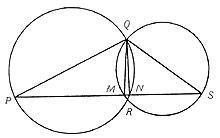
Dibujemos dos circunferencias que se cruzan en los puntos Q y R. Desde el punto Q se representan los diámetros de las circunferencias QP y QS. A continuación el segmento PS. Esto corta las circunferencias en dos puntos, M y N. (Ver imagen).
Los triángulos PNQ y SMQ están inscritos en semicircunferencia, siendo uno de sus lados el diámetro. Por lo tanto, se concluye que los ángulos PNQ y SMQ deben ser correctos, o lo que es lo mismo los rectángulos QM y QN son unidos al segmento PS, como queríamos demostrar.
Paradoja 2
El ángulo recto es igual al ángulo obtuso.
Sea ABCD cualquier rectángulo. Trazaremos por el punto B el segmento BE de longitud BC. Si representamos los puntos centrales de los rectángulos AB y DE, éstos se cruzarán en el punto P (Mira la imagen). A partir de este punto P construiremos los rectores PA, PB, PD y PE. En los triángulos DA y PUE las diferencias DA son iguales,
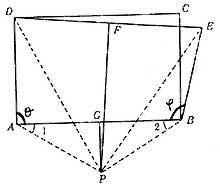
Porque así lo hemos elegido. También PA = PB y PD = PE, puesto que el punto P se encuentra en las uniones que pasan por el punto medio de los rectángulos DE y AB, lo que significa que es distante por un lado de los puntos A y B y por otro de los puntos D y E.
Dado que los lados de estos dos triángulos son iguales respectivamente, los triángulos deben ser iguales. Por tanto, los ángulos DAP y EBP son iguales. Como por el otro lado el triángulo PBA es isósceles (PA = PB), los ángulos 1 y 2 son iguales. De aquí sacamos que el ángulo recto y el ángulo obtuso son iguales.
Paradoja 3
Todos los puntos de un círculo se encuentran en su circunferencia.
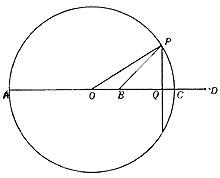
Sea B O un punto del círculo con centro. Dibujaremos el diámetro AC desde el punto B. Prolongando el diámetro AC tomaremos el punto D para que se cumpla la siguiente proporción
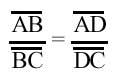
Construyamos la BD uniendo QP por el punto medio del segmento y representamos los rectángulos PO y PB por el punto P. Si el radio del círculo es r AB = r + OB y BC = r – OB, AD = r + OD y DC = OD – r. Proporción anterior por sustitución de estas igualdad
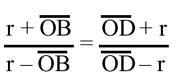
podemos escribir o (r + OB) (OD – r) = (OD + r) (r – OB). OB tras operaciones y simplificación. Obtenemos OD = r 2 y dado que para la imagen OB = QB – BQ y OD = OQ + QD, (OQ – BQ) (OQ + QD) = r 2 . Pero como Q es el punto medio del segmento BD, BQ = QD, sustituyendo esta última igualdad en el anterior, obtenemos r 2 = OQ 2 – BQ 2 (1).
Aplicando el teorema de Pitágoras a los triángulos OQP y BQP:
OP 2 = OQ 2 + PQ 2
BP 2 = BQ 2 + PQ 2
Ahora calculando por partes la diferencia entre ambas nivelaciones OP 2 – BP 2 = OQ 2 – BQ 2 , pero si OP = r es r 2 – BP 2 = OQ 2 – BQ 2 . Sustituyendo esta igualdad (1) por la igualdad tenemos r 2 = r 2 – BP 2 o BP 2 = 0. Por lo tanto, los puntos B y P deben coincidir, es decir, el punto B debe estar en la circunferencia.
Paradoja 4
Todo triángulo es isósceles.
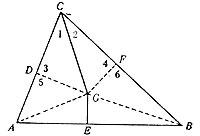
Sea el triángulo ABC. Dibujemos la bisectriz del ángulo Cfl y el punto medio del lado AB. Representaremos las uniones GD y GF, respectivamente, con los lados AC y BC desde el punto G en el que se cruzan ambas líneas. También los directos GA y GB. Los triángulos CGD y CGF son iguales, ya que la zona CG es común, 1fl = 2fl (construcción) y 3fl = 4fl (rectas). Por lo tanto DG = GF. En los triángulos GDA y GFB las rectas 5fl = 6fl, AG = BG (porque el triángulo IGP es isósceles) y como hemos demostrado anteriormente DG = GF. Por tanto, GDA y GFB son los mismos triángulos. De estas parejas de triángulos iguales se deduce CD = CF y AD = BF. Agregando estas igualdad por partes AD + CD = BF + CF o AC = BC, es decir, el triángulo es isósceles.
Paradoja 5
Comprobaremos que dos de los dos directos son iguales.
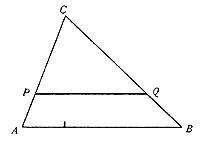
Sea ABC cualquier triángulo y PQ un rectángulo paralelo al lado AB (ver figura). Los triángulos ABC y PQC son similares. Por lo tanto
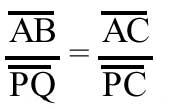
se cumple la proporción. De ahí AB . PC = AC . PQ. Multiplicando ambos apartados por (AB – PQ) tenemos:
AB 2 . PC – AB . PC . PQ = AC . PQ . AB – AC PQ 2
En esta igualdad AB . PC . PQ y AC . PQ . Si cambiamos de sección AB:
AB 2 . PC – AC. PQ . AB = AB . PC . PQ – AC. Obtenemos PQ 2. Ahora AB y PQ respectivamente extrayendo el factor AB (AB . PC – AC. PQ) = PQ (AB . PC – AC. se obtendrá (PQ) y (AB . PC – AC. Simplificando el PQ) en ambos apartados, obtenemos AB = PQ.
Paradoja 6
Veamos que 45° = 60° o 3 = 4. Utilizando el lado AB del triángulo equilátero ABC como hipotenusa, construyamos el triángulo recto ABD. Comprobamos que los ángulos ABC = 60º y ABD = 45º son iguales.
En la zona BC tomaremos el segmento BE de longitud BD. Sea F, el punto medio del segmento AD. Dibujemos la línea FE recta hasta que cortemos la extensión de la zona AB en el punto G. Uniremos directamente los puntos G y D. A continuación representaremos un rectángulo perpendicular a los puntos centrales de las direcciones GD y GE. Estas dos rectas se cortarán en el punto k. Asociaremos este punto K a los puntos G, D, E y B. (Ver imagen). La función actual consiste en demostrar que los triángulos KDB y KBE son iguales. Esto se debe a que KG = DC y KG = NC (ya que KDG y KGE son triángulos lisos). Por lo tanto NC = DC. Por otro lado, hemos seleccionado CV = BD y CJ es la parte común. Los dos triángulos, por tanto, son iguales. Por ello, nos vemos unos a otros
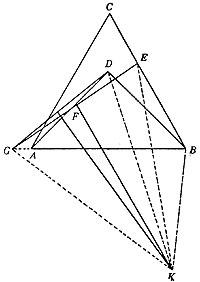
los ángulos correspondientes deben ser iguales, es decir, los ángulos KBD y CCI son iguales. Si eliminamos a éstos el ángulo VCC que es la parte común, obtendremos los ángulos ABD e VC que buscábamos. Escribiendo en radianes supondríamos /4 = /3 o 3 = 4
Paradoja 7
En esta última paradoja se incluye la geometría y el análisis, y dentro del análisis se incluye el concepto de limite. En la siguiente secuencia de imágenes aparece el problema que se produce en el infinito, es decir, al tomar el límite.
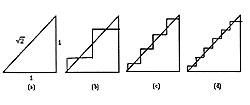
Como se observa en la figura (a), existe un triángulo recto isósceles con catetos de 1 unidad, siendo su hipotenusa 2 unidad. Las figuras (b), (c), (d) muestran los primeros temas de una sucesión de líneas quebradas. Por un lado, estas líneas están cada vez más cerca de la hipotenusa. En otras palabras, el hipotenus y las líneas se parecen cada vez más. Por otro lado, todas las líneas rotas tienen una longitud de 2. Siguiendo el procedimiento, las siguientes líneas tendrían la misma longitud. Es decir, siguiendo las imágenes, el límite de las líneas rotas es hipotenus. Sin embargo, siguiendo las longitudes, la longitud del límite de línea es 2 (debido a que la sucesión de longitudes es constante). La paradoja es que el límite de línea es hipotenusa, pero la longitud de la hipotenusa no es 2 ; es 2.





