Buscando número e

O número e é un número entre dous e tres. Se quixésemos escribir sabemos que a primeira cifra sería 2, tras esa primeira cifra deberiamos pór una coma e detrás de cómaa os decimais correspondentes a ese número: 718281... Empezamos a pór decimais, pero terminariamos? Nunca acabariamos. De feito, o número e ten un número infinito de decimais que non teñen periodicidade, é dicir, non se repiten. Por iso, en lugar de expresarse numericamente, represéntase mediante un símbolo. Do mesmo xeito que o número e, indícanse outros mediante letras. O máis famoso é o número.
O matemático Leonhard Euler decidiu que o símbolo do número e debía ser esta letra. Non está moi claro por que elixiu a letra e. Deron varias explicacións posibles. Un sostén que Euler deulle a primeira letra da palabra exponencial pola forte relación entre o número e e o exponencial. Segundo outras explicacións, elixiuna porque é a primeira letra do seu apelido (idea que hoxe está bastante descartada), ou porque era a primeira letra do alfabeto que non se utilizaba en matemáticas (as letras a, b, c e d eran moi frecuentes nas fórmulas matemáticas)... Sexa cal for o motivo, deulle ese nome e desde entón utilizouse ese número paira expresalo.
Ocultos en matemáticas

Euler, ademais de apuntarse, realizou un gran traballo sobre o número e. Definiu as súas propiedades cara a 1730. Ante el descubriu que os traballos realizados por varios matemáticos estaban relacionados co número e e baseouse neles paira definir as propiedades.
XVII. Os primeiros traballos realizáronse a principios do século XX e desde entón algúns matemáticos, nos seus cálculos, obtiveron o número e como resultado, pero non se deron conta de que todos estes resultados eran un número único. Por exemplo, en 1661 foi identificado por Christian Huygens. Estudando a curva xy = 1, quixo saber entre o número 1 e o outro número que ocupa una superficie de valor 1 (mirar a figura inferior). A este número chamoulle. Tratábase do número e de Euler.
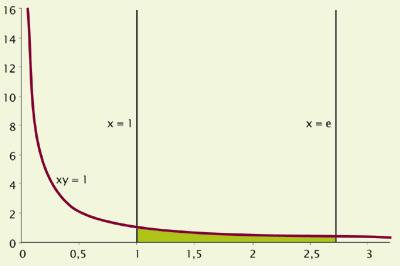
Aínda que tardaron tanto en descubrir e describir, o número e é hoxe moi común e utilizado. Adoita coñecerse por primeira vez en época de estudante, ligado a logaritmos neperianos. A partir de aí, algúns esquecen que o número e existe, pero paira outros se converte nunha ferramenta imprescindible.
Base de crecemento exponencial
Nalgúns oficios é necesario o número e, entre outros, paira aqueles que traballan con algo que aumenta ou diminúe exponencialmente. Por exemplo, paira médicos forenses. Por que? Porque grazas ao número e, medindo a temperatura dun morto, poden saber cando morreu esa persoa. Cando una persoa está viva, o seu metabolismo mantén constante a temperatura corporal ao redor dos 36ºC. No momento da súa morte, o corpo deixa de producir calor e o corpo empeza a perder temperatura exponencialmente até alcanzar a temperatura ambiental.
A alta temperatura do corpo no novo mes fai que nos primeiros minutos diminúa rapidamente. A medida que se arrefría, a perda de calor é cada vez máis lenta. Esta é a particularidade do descenso exponencial, é dicir, que o seu descenso nun determinado período de tempo depende do seu valor en cada momento. O crecemento exponencial é como o descenso: cando o valor é baixo, o crecemento tamén é pequeno, e a medida que aumenta, o crecemento tamén aumenta, e ademais aumenta moito!
En todo isto, onde está o número e? Pois ben, o número e é a base deste peculiar ritmo de crecemento. Se algo ten crecemento exponencial, matematicamente pódese expresar co número e e non con outro número. Por tanto, é imprescindible paira facer modelos de crecemento, estimacións, previsións... de algo. Por iso é tan importante.

Importante e omnipresente con crecemento exponencial. Os compostos químicos radioactivos desaparecen ao ritmo marcado polo número e. Isto é moi útil, por exemplo, paira os paleontólogos cando queren datar algunha pegada fósil. Miden o nivel de 14 isótopos de carbono radioactivo de trázalas e calculan o grao da pegada.
Tamén as poboacións de seres vivos (de calquera ser vivo, tanto de bacterias como de plantas e animais), que crecen baixo o número e mentres non teñen límites de crecemento. Outros exemplos son os que teñen un crecemento exponencial baixo o número e, desde o crecemento dunha pelota de neve en descenso, até os intereses que os bancos, ou sobre todo, cobran.
Máis aló do crecemento exponencial
O número e tamén aparece nalgúns casos alleos ao crecemento exponencial. Supoñamos que colgamos una cadea, una corda, un cable... entre dous postes, é dicir, que temos una catenaria (como cando colgan o fío condutor paira os trens ou a liña eléctrica da electricidade). A curva de cada tramo de cadea entre dous postes vén definida polo número e. A fórmula da curva é curiosa, xa que nos seus dous sumarios aparece o número e: e = (e x + e -x )/2 . Paira os enxeñeiros que están a deseñar este tipo de estruturas, por tanto, o número e é un compoñente a ter sempre en conta. As súas obras tamén dependen do número e.
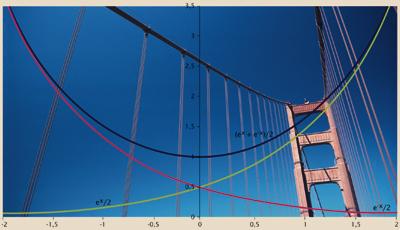
Non é ningún número e. No mundo que nos rodea aparece en máis do que creemos, polo menos en mortos, compostos radioactivos, poboacións de seres vivos, pelotas de neve, liñas eléctricas, pontes colgantes… e tamén no diñeiro que temos no banco! Aínda que moitas veces non nos damos conta, se buscamos atopariamos o número e en máis do que pensamos. É importante, sen dúbida.





