Looking for number e

The number e is a number between two and three. If we wanted to write we know that the first figure would be 2, after that first figure we should put a comma and behind the comma the decimals corresponding to that number: 718281... We started to make decimals, but would we end? We would never end. In fact, the number e has an infinite number of decimals that do not have periodicity, that is, they are not repeated. Therefore, instead of expressing itself numerically, it is represented by a symbol. Like the number e, others are indicated by letters. The most famous is the number.
Mathematician Leonhard Euler decided that the symbol of the number and should be this letter. It is not very clear why he chose the letter e. They have given several possible explanations. One holds that Euler gave him the first letter of the exponential word for the strong relationship between the number e and the exponential. According to other explanations, he chose it because it is the first letter of his surname (idea that today is quite discarded), or because it was the first letter of the alphabet that was not used in mathematics (letters a, b, c and d were very frequent in mathematical formulas)... Whatever the reason, he gave him that name and since then he has used that number to express it.
Hidden in mathematics

Euler, in addition to signing up, did a great job on number e. It defined its properties around 1730. Before him he discovered that the works performed by several mathematicians were related to the number e and was based on them to define the properties.
XVII. The first works were performed in the early 20th century and since then some mathematicians, in their calculations, obtained the number and as a result, but did not realize that all these results were a unique number. For example, in 1661 he was identified by Christian Huygens. Studying the xy = 1 curve, he wanted to know between the number 1 and the other number that occupies a surface of value 1 (look at the lower figure). He called this number. This was the number e of Euler.
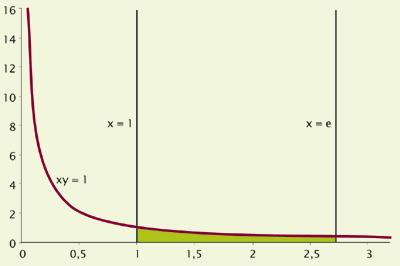
Although they took so long to discover and describe, the number e is now very common and used. It is usually known for the first time in student age, linked to Neperian logarithms. From there, some forget that the number and exists, but for others it becomes an indispensable tool.
Exponential growth base
In some trades it is necessary the number e, among others, for those who work with something that increases or decreases exponentially. For example, forensic doctors. Why? Because thanks to the number e, measuring the temperature of a dead person, they can know when that person died. When a person is alive, his metabolism keeps the body temperature constant around 36ºC. At the time of his death, the body ceases to produce heat and the body begins to lose temperature exponentially until it reaches the ambient temperature.
The high body temperature in the new month makes in the first few minutes decrease quickly. As it cools down, heat loss is getting slower. This is the particularity of the exponential decline, that is, its decrease in a certain period of time depends on its value at each moment. Exponential growth is like the decline: when value is low, growth is also small, and as growth increases, growth also increases, and also increases a lot!
In all this, where is the number e? Well, the number e is the basis of this peculiar pace of growth. If something has exponential growth, mathematically it can be expressed with the number e and not with another number. Therefore, it is essential to make growth models, estimates, forecasts... of something. That is why it is so important.

Important and omnipresent with exponential growth. Radioactive chemical compounds disappear at the rate marked by the number e. This is very useful, for example, for paleontologists when they want to date a fossil footprint. They measure the level of 14 trace radioactive carbon isotopes and calculate the grade of the footprint.
Also the populations of living beings (of any living being, both of bacteria, plants and animals), that grow under the number e while they have no limits of growth. Other examples are those that have exponential growth under the number e, from the growth of a snowball in decline, to the interests that banks, or above all, charge.
Beyond exponential growth
The number and also appears in some cases alien to exponential growth. Suppose we hang a chain, a rope, a cable... between two poles, that is, we have a catenary (such as when they hang the conductive thread for trains or the electricity line). The curve of each chain stretch between two poles is defined by number e. The curve formula is curious, since in its two summaries the number e: y = (e x + e -x)/2 appears. For engineers who are designing such structures, therefore, the number e is a component to always consider. His works also depend on number e.
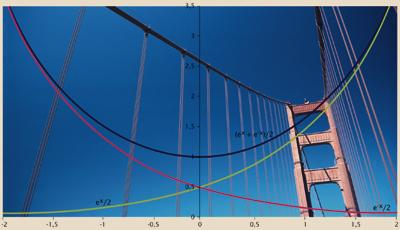
It is no number e. In the world around us it appears in more than we believe, at least in dead, radioactive compounds, populations of living beings, snowballs, power lines, hanging bridges… and also in the money we have in the bank! Although many times we do not realize, if we seek we would find the number e in more than we think. It is certainly important.





