Buscando número e

El número e es un número entre dos y tres. Si quisiéramos escribir sabemos que la primera cifra sería 2, tras esa primera cifra deberíamos poner una coma y detrás de la coma los decimales correspondientes a ese número: 718281... Empezamos a poner decimales, pero ¿terminaríamos? Nunca acabaríamos. De hecho, el número e tiene un número infinito de decimales que no tienen periodicidad, es decir, no se repiten. Por ello, en lugar de expresarse numéricamente, se representa mediante un símbolo. Al igual que el número e, se indican otros mediante letras. El más famoso es el número.
El matemático Leonhard Euler decidió que el símbolo del número e debía ser esta letra. No está muy claro por qué eligió la letra e. Han dado varias explicaciones posibles. Uno sostiene que Euler le dio la primera letra de la palabra exponencial por la fuerte relación entre el número e y el exponencial. Según otras explicaciones, la eligió porque es la primera letra de su apellido (idea que hoy está bastante descartada), o porque era la primera letra del alfabeto que no se utilizaba en matemáticas (las letras a, b, c y d eran muy frecuentes en las fórmulas matemáticas)... Sea cual sea el motivo, le dio ese nombre y desde entonces se ha utilizado ese número para expresarlo.
Ocultos en matemáticas

Euler, además de apuntarse, realizó un gran trabajo sobre el número e. Definió sus propiedades hacia 1730. Ante él descubrió que los trabajos realizados por varios matemáticos estaban relacionados con el número e y se basó en ellos para definir las propiedades.
XVII. Los primeros trabajos se realizaron a principios del siglo XX y desde entonces algunos matemáticos, en sus cálculos, obtuvieron el número e como resultado, pero no se dieron cuenta de que todos estos resultados eran un número único. Por ejemplo, en 1661 fue identificado por Christian Huygens. Estudiando la curva xy = 1, quiso saber entre el número 1 y el otro número que ocupa una superficie de valor 1 (mirar la figura inferior). A este número le llamó. Se trataba del número e de Euler.
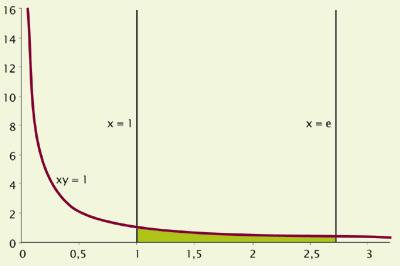
Aunque tardaron tanto en descubrir y describir, el número e es hoy muy común y utilizado. Suele conocerse por primera vez en época de estudiante, ligado a logaritmos neperianos. A partir de ahí, algunos olvidan que el número e existe, pero para otros se convierte en una herramienta imprescindible.
Base de crecimiento exponencial
En algunos oficios es necesario el número e, entre otros, para aquellos que trabajan con algo que aumenta o disminuye exponencialmente. Por ejemplo, para médicos forenses. ¿Por qué? Porque gracias al número e, midiendo la temperatura de un muerto, pueden saber cuándo murió esa persona. Cuando una persona está viva, su metabolismo mantiene constante la temperatura corporal en torno a los 36ºC. En el momento de su muerte, el cuerpo deja de producir calor y el cuerpo empieza a perder temperatura exponencialmente hasta alcanzar la temperatura ambiental.
La alta temperatura del cuerpo en el nuevo mes hace que en los primeros minutos disminuya rápidamente. A medida que se enfría, la pérdida de calor es cada vez más lenta. Esta es la particularidad del descenso exponencial, es decir, que su descenso en un determinado periodo de tiempo depende de su valor en cada momento. El crecimiento exponencial es como el descenso: cuando el valor es bajo, el crecimiento también es pequeño, y a medida que aumenta, el crecimiento también aumenta, ¡y además aumenta mucho!
En todo esto, ¿dónde está el número e? Pues bien, el número e es la base de este peculiar ritmo de crecimiento. Si algo tiene crecimiento exponencial, matemáticamente se puede expresar con el número e y no con otro número. Por lo tanto, es imprescindible para hacer modelos de crecimiento, estimaciones, previsiones... de algo. Por eso es tan importante.

Importante y omnipresente con crecimiento exponencial. Los compuestos químicos radiactivos desaparecen al ritmo marcado por el número e. Esto es muy útil, por ejemplo, para los paleontólogos cuando quieren fechar alguna huella fósil. Miden el nivel de 14 isótopos de carbono radiactivo de las trazas y calculan el grado de la huella.
También las poblaciones de seres vivos (de cualquier ser vivo, tanto de bacterias como de plantas y animales), que crecen bajo el número e mientras no tienen límites de crecimiento. Otros ejemplos son los que tienen un crecimiento exponencial bajo el número e, desde el crecimiento de una pelota de nieve en descenso, hasta los intereses que los bancos, o sobre todo, cobran.
Más allá del crecimiento exponencial
El número e también aparece en algunos casos ajenos al crecimiento exponencial. Supongamos que colgamos una cadena, una cuerda, un cable... entre dos postes, es decir, que tenemos una catenaria (como cuando cuelgan el hilo conductor para los trenes o la línea eléctrica de la electricidad). La curva de cada tramo de cadena entre dos postes viene definida por el número e. La fórmula de la curva es curiosa, ya que en sus dos sumarios aparece el número e: y = (e x + e -x )/2 . Para los ingenieros que están diseñando este tipo de estructuras, por tanto, el número e es un componente a tener siempre en cuenta. Sus obras también dependen del número e.
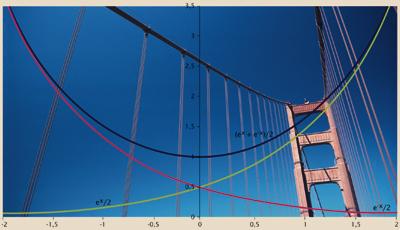
No es ningún número e. En el mundo que nos rodea aparece en más de lo que creemos, al menos en muertos, compuestos radiactivos, poblaciones de seres vivos, pelotas de nieve, líneas eléctricas, puentes colgantes… ¡y también en el dinero que tenemos en el banco! Aunque muchas veces no nos damos cuenta, si buscamos encontraríamos el número e en más de lo que pensamos. Es importante, sin duda.





