Recherche numéro e

Le nombre e est un nombre entre deux et trois. Si nous voulions écrire nous savons que le premier chiffre serait 2, après ce premier chiffre nous devrions mettre une virgule et derrière la virgule les décimales correspondant à ce nombre: 718281... Nous avons commencé à mettre des décimales, mais finirons-nous? Nous n'aurions jamais fini. En fait, le nombre e a un nombre infini de décimales qui n'ont pas de périodicité, c'est-à-dire qui ne se répètent pas. Ainsi, au lieu de s'exprimer numériquement, elle est représentée par un symbole. Comme le nombre e, d'autres sont indiqués par des lettres. Le plus célèbre est le nombre.
Le mathématicien Leonhard Euler a décidé que le symbole du nombre et devrait être cette lettre. Il n'est pas très clair pourquoi il a choisi la lettre e. Ils ont donné plusieurs explications possibles. On soutient qu'Euler lui a donné la première lettre du mot exponentiel par la relation forte entre le nombre et l'exponentiel. Selon d'autres explications, il a choisi parce que c'est la première lettre de son nom (idée qui est aujourd'hui assez écartée), ou parce qu'il était la première lettre de l'alphabet qui n'était pas utilisé en mathématiques (les lettres a, b, c et d étaient très fréquentes dans les formules mathématiques)... Quelle que soit la raison, il lui a donné ce nom et depuis ce numéro a été utilisé pour l'exprimer.
Caché en mathématiques

Euler, en plus de s'inscrire, a fait un grand travail sur le nombre e. Il définit ses propriétés vers 1730. Avant il a découvert que les travaux réalisés par plusieurs mathématiciens ont été liés au nombre e et a été basé sur eux pour définir les propriétés.
XVII. Les premiers travaux ont été effectués au début du XXe siècle et depuis lors, certains mathématiciens, dans leurs calculs, ont obtenu le nombre et en conséquence, mais n'ont pas réalisé que tous ces résultats étaient un nombre unique. Par exemple, en 1661, il a été identifié par Christian Huygens. En étudiant la courbe xy = 1, il a voulu savoir entre le numéro 1 et l'autre numéro qui occupe une surface de valeur 1 (voir la figure inférieure). Ce nombre a été appelé. Il s'agissait du numéro e d'Euler.
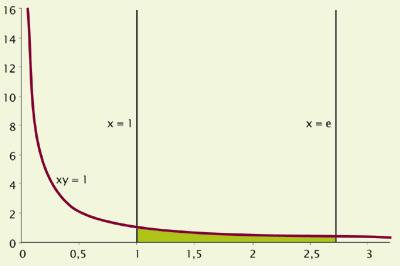
Bien qu'ils aient pris tellement à découvrir et décrire, le nombre e est aujourd'hui très commun et utilisé. Il est connu pour la première fois en période d'étudiant, lié aux logarithmes népalais. De là, certains oublient que le nombre et existe, mais pour d'autres, il devient un outil indispensable.
Base de croissance exponentielle
Dans certains métiers, le nombre est nécessaire, entre autres, pour ceux qui travaillent avec quelque chose qui augmente ou diminue de façon exponentielle. Par exemple, pour les médecins légistes. Pourquoi ? Parce que grâce au nombre e, en mesurant la température d'un mort, ils peuvent savoir quand cette personne est morte. Quand une personne est vivante, son métabolisme maintient la température corporelle constante autour de 36 ° C. Au moment de sa mort, le corps cesse de produire de la chaleur et le corps commence à perdre une température exponentielle jusqu'à atteindre la température ambiante.
La température élevée du corps dans le nouveau mois fait diminuer rapidement dans les premières minutes. Comme il refroidit, la perte de chaleur devient de plus en plus lente. C'est la particularité de la descente exponentielle, c'est-à-dire que sa descente dans une période donnée dépend de sa valeur à chaque moment. La croissance exponentielle est comme la baisse: quand la valeur est faible, la croissance est aussi petite, et comme elle augmente, la croissance augmente aussi, et en plus elle augmente beaucoup!
Dans tout cela, où est le numéro e? Eh bien, le nombre e est la base de ce rythme particulier de croissance. Si quelque chose a une croissance exponentielle, on peut mathématiquement exprimer avec le nombre et non avec un autre nombre. Il est donc indispensable de faire des modèles de croissance, des estimations, des prévisions... de quelque chose. C'est pourquoi il est si important.

Important et omniprésent avec une croissance exponentielle. Les composés chimiques radioactifs disparaissent au rythme marqué par le nombre e. Ceci est très utile, par exemple, pour les paléontologues quand ils veulent dater une trace fossile. Ils mesurent le niveau de 14 isotopes de carbone radioactif des traces et calculent le degré d'empreinte.
Aussi les populations d'êtres vivants (de tout être vivant, aussi bien des bactéries que des plantes et des animaux), qui grandissent sous le nombre et tant qu'elles n'ont pas de limites de croissance. D'autres exemples sont ceux qui ont une croissance exponentielle sous le nombre e, de la croissance d'une boule de neige en descente, aux intérêts que les banques, ou surtout, encaissent.
Au-delà de la croissance exponentielle
Le nombre e apparaît également dans certains cas étrangers à la croissance exponentielle. Supposons que nous accrochions une chaîne, une corde, un câble... entre deux poteaux, c'est-à-dire que nous avons une caténaire (comme quand ils pendent le fil conducteur pour les trains ou la ligne électrique de l'électricité). La courbe de chaque section de chaîne entre deux colonnes est définie par le nombre e. La formule de la courbe est curieuse, puisque dans ses deux sommaires apparaît le nombre e: y = (e x + e -x )/2 . Pour les ingénieurs qui conçoivent ce type de structures, par conséquent, le nombre e est un composant à prendre toujours en compte. Ses œuvres dépendent également du nombre e.
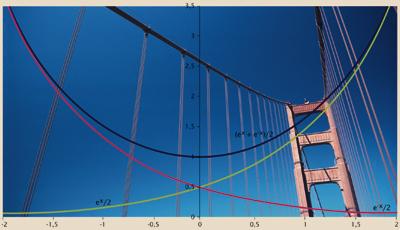
Ce n'est aucun nombre e. Dans le monde qui nous entoure, il apparaît dans plus que nous le croyons, au moins dans les morts, les composés radioactifs, les populations d'êtres vivants, les boules de neige, les lignes électriques, les ponts suspendus… et aussi dans l'argent que nous avons sur la banque ! Bien que nous ne nous rendions souvent pas compte, si nous cherchons, nous trouverions le numéro et plus que ce que nous pensons. Il est important, sans doute.





