Diagramas lóxicos (II)
No número de xuño explicáronse algunhas das posibilidades do diagrama de Venn. Pero este non é o único sistema inventado. Como veremos a continuación, existen outros sistemas paira utilizar na lóxica de clases e de proposta.
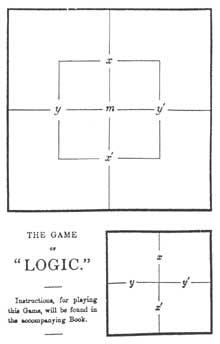
Outro sistema é o ideado polo prestixioso escritor Lewis Carroll. Lewis non se valeu de círculos senón de cadrados. Explicarémolas tal e como as usaba. Dividía un cadrado en catro casas iguais paira incluír todas as combinacións de X e E. Posteriormente, paira o uso da terceira materia incluía dentro deste cadrado outro máis pequeno (Figura 1). Así aparecían todas as combinacións posibles entre X, E e M. Lewis utilizaba X’ (non X) paira expresar a negación do termo X. Así a metade superior do cadrado é X, a metade inferior é X’ (non X). A parte esquerda é E, a dereita é E, mentres que a parte interior do cadrado pequeno é M o exterior é M’.
Marcaba con fichas as rexións adecuadas paira traducir as premisas dun silogismo. Por iso, nas rexións con elementos puña a ficha vermella e nas sen elementos a ficha gris. Nas dúas rexións contiguas había elementos pero nas que non sabía, puña a ficha vermella na liña fronteiriza.
Podería tentar resolver o problema típico de Lewis:

Se as fichas colócanse seguindo as regras de Lewis, pódese concluír que “ningunha E é X” é correcta, é dicir, a ningún ruiseñor o azucre molesto. Os lóxicos clásicos non aceptarían leste silogismo.
O diagrama de Lewis pode estenderse a n temas. O propio Lewis móstranos no seu libro Symbolic Logyc un diagrama de 256 casas adaptadas a oito temas.
O gráfico de Lewis aparece por primeira vez en The Game of Logyc. Xunto co folleto entregábase aos compradores una cartón co diagrama de Lewis e una bolsa con nove fichas (catro vermellas e cinco grises), tal e como se mostra na figura 1.
O diagrama de Lewis é do tipo de diagramas que inventou o claustral da Universidade Alland Marquand John Hopkins co obxectivo de estendelo a n temas no diagrama de tres temas.
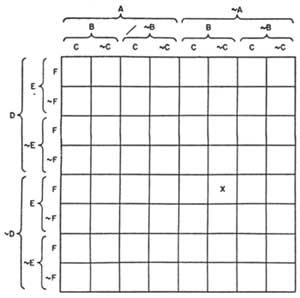
Marquand dividía un cadrado en casas iguais en función do número de artigos. Na figura 10 pódese ver o diagrama para 6 temas. A x que aparece nela indica a clase &AB&C&DEF (nin A, B, nin C, nin D, E, F). Este tipo de gráfico tamén permite resolver problemas de n temas, escurecendo os cadrados baleiros e marcando cunha X os de elementos.
Seguindo este tipo de diagramas propuxéronse diferentes divisións do cadrado que non se mencionan aquí.
Outro gran matemático e articulista que tratou de representar o cálculo da proposta mediante diagramas é o propio Martin Gardner, do libro titulado “Máquinas e diagramas lóxicos”, cuxa esencia sacamos deste artigo.
Martín propón un diagrama en rede. Cada tema do problema exprésase mediante dúas rectas verticais e paralelas. Cada un indicará un título. Por convenio o esquerdo será verdadeiro e o dereito falso. (Figura 3). Se un tema é certo, indicarase una X sobre a recta esquerda. Si é falsa, na da dereita. Os enunciados que relacionan dous temas expresarémolos directamente de forma horizontal, segundo o cadro do enunciado. A estes directos chamarémoslles pontes, xa que entre dous temas cumpren o papel de ponte. Na figura 4 móstranse algúns exemplos: Na figura 4a) móstranse todos os rectos que poden unir dous temas fronte aos que se atopan os valores da táboa correspondente. A ponte superior indica no diagrama 4b) a relación A B, “A e B”, é dicir, das catro posibilidades só se pode encher a CE. Con todo, a ponte inferior indica a relación A B, &“A e non B”. No diagrama 4d) temos o enunciado A, “A só se B”. O diagrama 4e) mostra o correspondente ao enunciado A B, “ou A ou B, pero non ambos á vez”.
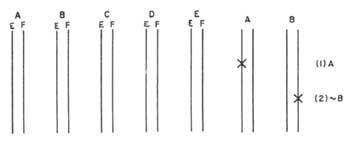
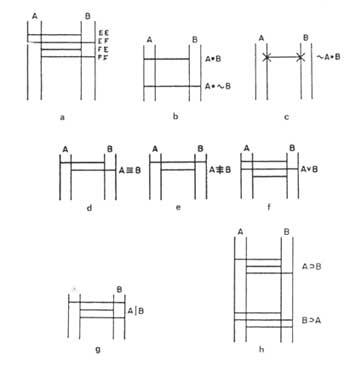
Si nun enunciado tivésemos unha soa ponte, por exemplo &A B, “non A e B”, sería certo e escribiriamos x nos dous extremos da ponte. Determinando o valor de ambas as cuestións 4c). A|B, “A e B non son simultáneos de verdade”, no diagrama do enunciado (g) aparecen tres pontes; A B, “A e B”, que faltan ao enunciado. Por tanto, diremos que estes dous enunciados son negados entre si. Os enunciados A B “Si A entón B” e B A “si B entón A” aparecen no diagrama da figura 4h). Este tipo de enunciados non teñen outro significado que o indicado no cálculo de proposta polas pontes do diagrama. Por tanto, una proposición real só pode implicar una proposición real. Con todo, as proposicións falsas poden implicar tanto a proposición real como a proposición falsa.
Vimos todas as relacións binarias entre dous temas mediante diagramas en rede. Dúas relacións binarias serán equivalentes si nos seus diagramas de rede aparecen os mesmos pontes.
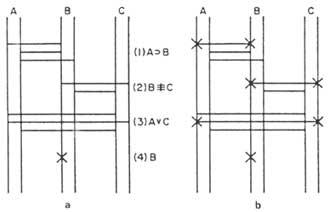
Vexamos o problema que propón Martín, que está composto polas seguintes premisas:

O primeiro paso consiste en representar o diagrama de catro premisas (figura 5 a)). O segundo paso consiste en explorar a estrutura da “estada”, a fin de determinar si quedan perfectamente determinados os valores dos elementos A e C: Como o valor de B é coñecido, comezaremos na recta real de B. Temos que buscar unha ponte que termina nesta recta. Esta ponte deberá cumprir que desde a recta final do outro extremo non se pode arrincar outra ponte que nos leve a contradición co anterior. Por exemplo, dúas pontes de 1 premisa finalizan en directo. Se seguimos o segundo, diríxese cara á recta falsa de A. Por tanto, teriamos una contradición. Se eliximos o superior, chegariamos a contradición, despois de percorrer un camiño máis longo.
Por tanto, a única ponte que non nos contradi é de 2 premisas, polo que debemos pasar por el escribindo una x nos dous extremos da ponte. Por tanto, 4 e 2 premisas obrígannos a dicir que c é falsa. A falsa recta de C remata unha única ponte de 3 premisas. Por tanto, nese extremo da ponte tamén escribiremos x. Cruzando a ponte de 3 premisas, chegaremos á recta real de A, onde poremos outra x. Conseguimos falso C e real A. Con todo, debemos seguir o estudo paira asegurar que non chegaremos á contradición. A verdadeira recta de A, e a única ponte que non nos contradi chega á premisa 1. Escribimos una x no extremo esquerdo desta ponte. Se cruzamos a ponte chegaremos á verdadeira recta de B sen atopar contradicións. Nela colocaremos outra x, pechando así o percorrido. Teremos entón a figura 5b).
Se queremos analizar outros camiños, verás que non hai outra posibilidade sen contradicións. Concluímos, por tanto, que A é verdadeiro, B é verdadeiro e C falso.
Aquí deixámosche o problema máis difícil para que o tentes:
1 En agosto, ou levo o chapeu ou me deixo a cabeza baleira.
2 Nunca vou descabezado en agosto se me poño gravata.
3 En agosto levo o chapeu ou a gravata e ás veces os dous
Paira facilitar o exame recomendámosche os seguintes temas:
A En agosto levo o chapeu
B En agosto levo gravata
C Agosto en branco
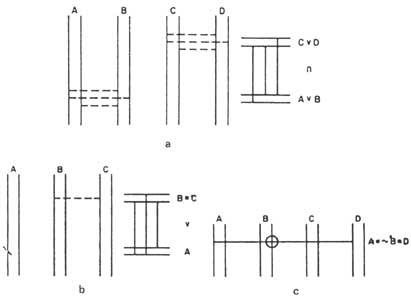
Tamén se poden obter diagramas de enunciados compostos. Martin, a modo de exemplo, móstranos no seu libro (A v B) o diagrama do enunciado (C v D) (Figura 6a). Nos diagramas dos enunciados (A v B) e (C v D) represéntanse as pontes por partes paira indicar que son provisionais. Se logo soubésemos que son certas, representariámolas cunha liña completa. En caso de ser falsos, poderían eliminarse e representariamos con liñas completas as pontes que faltan (os correspondentes á denegación).
A relación de implicación represéntase debuxando rectas horizontais xunto aos diagramas dos enunciados (A v B) e (C v D), dous pares á altura dos enunciados. Agora supomos que a recta inferior é certa. Entre estas catro rectas horizontais representaremos as pontes de implicación. Porque non hai dúbida da súa validez.
Si en lugar da v B tivésemos un tema simple, por exemplo A, paira expresar a súa provisionalidade, poriamos en verdadeira recta \(metade de x). Se logo resultase falso, borrariámolo e anotariamos outra vez en x. Se volvese ser certo, acabariamos x.
No diagrama 6b) (B C) aparece o enunciado v A).
Poderiamos representar una cadea de temas relacionados coas mesmas relacións marcando directamente o círculo 0 correspondente aos temas que aparecen na cadea. Por exemplo, o diagrama da cadea A B &D pódese ver na figura 6c).