Diagramas lógicos (II)
En el número de junio se explicaron algunas de las posibilidades del diagrama de Venn. Pero este no es el único sistema inventado. Como veremos a continuación, existen otros sistemas para utilizar en la lógica de clases y de propuesta.
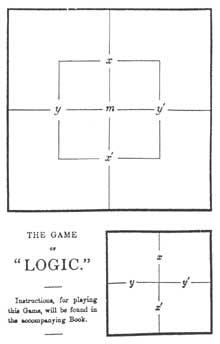
Otro sistema es el ideado por el prestigioso escritor Lewis Carroll. Lewis no se valió de círculos sino de cuadrados. Las explicaremos tal y como las usaba. Dividía un cuadrado en cuatro casillas iguales para incluir todas las combinaciones de X e Y. Posteriormente, para el uso de la tercera materia incluía dentro de este cuadrado otro más pequeño (Figura 1). Así aparecían todas las combinaciones posibles entre X, Y y M. Lewis utilizaba X’ (no X) para expresar la negación del término X. Así la mitad superior del cuadrado es X, la mitad inferior es X’ (no X). La parte izquierda es Y, la derecha es Y, mientras que la parte interior del cuadrado pequeño es M el exterior es M’.
Marcaba con fichas las regiones adecuadas para traducir las premisas de un silogismo. Por ello, en las regiones con elementos ponía la ficha roja y en las sin elementos la ficha gris. En las dos regiones contiguas había elementos pero en las que no sabía, ponía la ficha roja en la línea fronteriza.
Podría intentar resolver el problema típico de Lewis:

Si las fichas se colocan siguiendo las reglas de Lewis, se puede concluir que “ninguna Y es X” es correcta, es decir, a ningún ruiseñor el azúcar molesta. Los lógicos clásicos no aceptarían este silogismo.
El diagrama de Lewis puede extenderse a n temas. El propio Lewis nos muestra en su libro Symbolic Logyc un diagrama de 256 casillas adaptadas a ocho temas.
El gráfico de Lewis aparece por primera vez en The Game of Logyc. Junto con el folleto se entregaba a los compradores una tarjeta con el diagrama de Lewis y una bolsa con nueve fichas (cuatro rojas y cinco grises), tal y como se muestra en la figura 1.
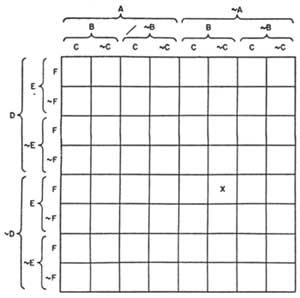
El diagrama de Lewis es del tipo de diagramas que inventó el claustral de la Universidad Alland Marquand John Hopkins con el objetivo de extenderlo a n temas en el diagrama de tres temas.
Marquand dividía un cuadrado en casillas iguales en función del número de artículos. En la figura 10 se puede ver el diagrama para 6 temas. La x que aparece en ella indica la clase &AB&C&DEF (ni A, B, ni C, ni D, E, F). Este tipo de gráfico también permite resolver problemas de n temas, oscureciendo los cuadrados vacíos y marcando con una X los de elementos.
Siguiendo este tipo de diagramas se han propuesto diferentes divisiones del cuadrado que no se mencionan aquí.
Otro gran matemático y articulista que ha tratado de representar el cálculo de la propuesta mediante diagramas es el propio Martin Gardner, del libro titulado “Máquinas y diagramas lógicos”, cuya esencia hemos sacado de este artículo.
Martín propone un diagrama en red. Cada tema del problema se expresa mediante dos rectas verticales y paralelas. Cada uno indicará un título. Por convenio el izquierdo será verdadero y el derecho falso. (Figura 3). Si un tema es cierto, se indicará una X sobre la recta izquierda. Si es falsa, en la de la derecha. Los enunciados que relacionan dos temas los expresaremos directamente de forma horizontal, según el cuadro del enunciado. A estos directos les llamaremos puentes, ya que entre dos temas cumplen el papel de puente. En la figura 4 se muestran algunos ejemplos: En la figura 4a) se muestran todos los rectos que pueden unir dos temas frente a los que se encuentran los valores de la tabla correspondiente. El puente superior indica en el diagrama 4b) la relación A B, “A y B”, es decir, de las cuatro posibilidades sólo se puede rellenar la CE. Sin embargo, el puente inferior indica la relación A &B, “A y no B”. En el diagrama 4d) tenemos el enunciado A, “A sólo si B”. El diagrama 4e) muestra el correspondiente al enunciado A B, “o A o B, pero no ambos a la vez”.
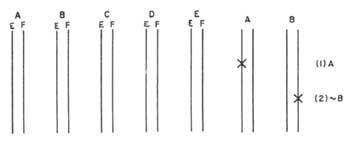
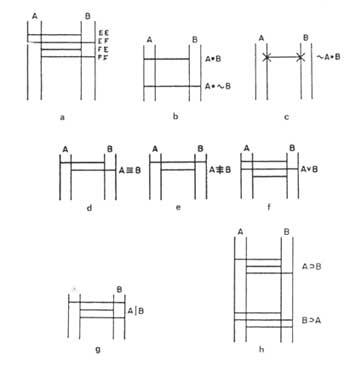
Si en un enunciado tuviéramos un solo puente, por ejemplo &A B, “no A y B”, sería cierto y escribiríamos x en los dos extremos del puente. Determinando el valor de ambas cuestiones 4c). A|B, “A y B no son simultáneos de verdad”, en el diagrama del enunciado (g) aparecen tres puentes; A B, “A y B”, que faltan al enunciado. Por tanto, diremos que estos dos enunciados son negados entre sí. Los enunciados A B “Si A entonces B” y B A “si B entonces A” aparecen en el diagrama de la figura 4h). Este tipo de enunciados no tienen otro significado que el indicado en el cálculo de propuesta por los puentes del diagrama. Por tanto, una proposición real sólo puede implicar una proposición real. Sin embargo, las proposiciones falsas pueden implicar tanto la proposición real como la proposición falsa.
Hemos visto todas las relaciones binarias entre dos temas mediante diagramas en red. Dos relaciones binarias serán equivalentes si en sus diagramas de red aparecen los mismos puentes.
Veamos el problema que propone Martín, que está compuesto por las siguientes premisas:

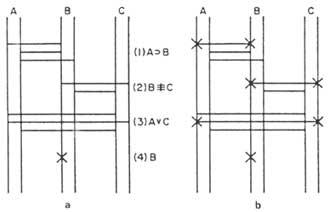
El primer paso consiste en representar el diagrama de cuatro premisas (figura 5 a)). El segundo paso consiste en explorar la estructura del “andamio”, a fin de determinar si quedan perfectamente determinados los valores de los elementos A y C: Como el valor de B es conocido, comenzaremos en la recta real de B. Tenemos que buscar un puente que termina en esta recta. Este puente deberá cumplir que desde la recta final del otro extremo no se puede arrancar otro puente que nos lleve a contradicción con el anterior. Por ejemplo, dos puentes de 1 premisa finalizan en directo. Si seguimos el segundo, se dirige hacia la recta falsa de A. Por lo tanto, tendríamos una contradicción. Si elegimos el superior, llegaríamos a contradicción, después de haber recorrido un camino más largo.
Por lo tanto, el único puente que no nos contradice es de 2 premisas, por lo que debemos pasar por él escribiendo una x en los dos extremos del puente. Por tanto, 4 y 2 premisas nos obligan a decir que c es falsa. La falsa recta de C remata un único puente de 3 premisas. Por lo tanto, en ese extremo del puente también escribiremos x. Cruzando el puente de 3 premisas, llegaremos a la recta real de A, donde pondremos otra x. Hemos conseguido falso C y real A. Sin embargo, debemos seguir el estudio para asegurar que no llegaremos a la contradicción. La verdadera recta de A, y el único puente que no nos contradice llega a la premisa 1. Escribimos una x en el extremo izquierdo de este puente. Si cruzamos el puente llegaremos a la verdadera recta de B sin encontrar contradicciones. En ella colocaremos otra x, cerrando así el recorrido. Tendremos entonces la figura 5b).
Si queremos analizar otros caminos, verás que no hay otra posibilidad sin contradicciones. Concluimos, por tanto, que A es verdadero, B es verdadero y C falso.
Aquí te dejamos el problema más difícil para que lo intentes:
1 En agosto, o llevo el sombrero o me dejo la cabeza vacía.
2 Nunca voy descabezado en agosto si me pongo corbata.
3 En agosto llevo el sombrero o la corbata y a veces los dos
Para facilitar el examen te recomendamos los siguientes temas:
A En agosto llevo el sombrero
B En agosto llevo corbata
C Agosto en blanco
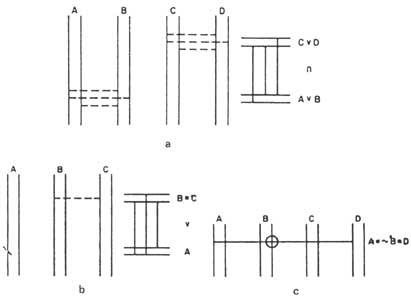
También se pueden obtener diagramas de enunciados compuestos. Martin, a modo de ejemplo, nos muestra en su libro (A v B) el diagrama del enunciado (C v D) (Figura 6a). En los diagramas de los enunciados (A v B) y (C v D) se representan los puentes por partes para indicar que son provisionales. Si luego supiéramos que son ciertas, las representaríamos con una línea completa. En caso de ser falsos, podrían eliminarse y representaríamos con líneas completas los puentes que faltan (los correspondientes a la denegación).
La relación de implicación se representa dibujando rectas horizontales junto a los diagramas de los enunciados (A v B) y (C v D), dos pares a la altura de los enunciados. Ahora suponemos que la recta inferior es cierta. Entre estas cuatro rectas horizontales representaremos los puentes de implicación. Porque no hay duda de su validez.
Si en lugar de A v B tuviéramos un tema simple, por ejemplo A, para expresar su provisionalidad, pondríamos en verdadera recta \(mitad de x). Si luego resultara falso, lo borraríamos y anotaríamos otra vez en x. Si volviera a ser cierto, acabaríamos x.
En el diagrama 6b) (B C) aparece el enunciado v A).
Podríamos representar una cadena de temas relacionados con las mismas relaciones marcando directamente el círculo 0 correspondiente a los temas que aparecen en la cadena. Por ejemplo, el diagrama de la cadena A &B D se puede ver en la figura 6c).