Diagrammes logiques (II)
Quelques possibilités du diagramme de Venn ont été expliquées dans le numéro de juin. Mais ce n'est pas le seul système inventé. Comme nous le verrons ci-dessous, il existe d'autres systèmes à utiliser dans la logique de classes et de proposition.
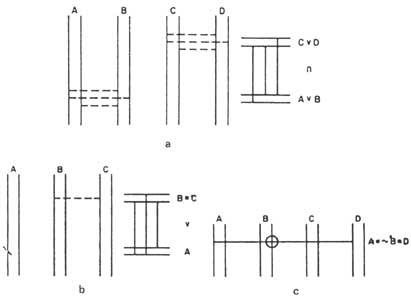
Un autre système est celui conçu par le prestigieux écrivain Lewis Carroll. Lewis n'a pas utilisé des cercles mais des carrés. Nous les expliquerons tel qu'il les utilisait. Il divisait un carré en quatre cases identiques pour inclure toutes les combinaisons de X et Y. Plus tard, pour l'utilisation de la troisième matière contenait dans ce carré un autre plus petit (Figure 1). Ainsi apparaissaient toutes les combinaisons possibles entre X, Y et M. Lewis utilisait X’ (pas X) pour exprimer le déni du terme X. Ainsi la moitié supérieure du carré est X, la moitié inférieure est X’ (pas X). La partie gauche est Y, la droite est Y, alors que la partie intérieure du petit carré est M l'extérieur est M’.
Il marquait avec des fiches les régions appropriées pour traduire les prémisses d'un syllogisme. C'est pourquoi, dans les régions avec des éléments, il mettait la fiche rouge et dans celles sans éléments la fiche grise. Dans les deux régions contiguës, il y avait des éléments mais dans lesquels il ne savait pas, il mettait la fiche rouge sur la ligne frontalière.
Vous pourriez essayer de résoudre le problème typique de Lewis:

Si les tuiles sont placées selon les règles de Lewis, on peut conclure que «aucun Y est X» est correct, c'est-à-dire à aucun rossignol le sucre ennuyeux. Les logiques classiques n'accepteraient pas ce syllogisme.
Le diagramme de Lewis peut être étendu à n thèmes. Lewis lui-même nous montre dans son livre Symbolic Logyc un diagramme de 256 cases adapté à huit thèmes.
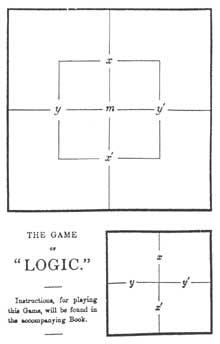
Le graphique Lewis apparaît pour la première fois dans The Game of Logyc. Avec la brochure, une carte contenant le diagramme de Lewis et un sac contenant neuf fiches (quatre rouges et cinq gris) étaient livrées aux acheteurs, comme le montre la figure 1.
Le diagramme de Lewis est du type de diagrammes qui a inventé le claustral de l'Université Alland Marquand John Hopkins dans le but de l'étendre à n thèmes dans le diagramme de trois thèmes.
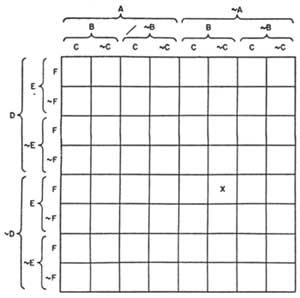
Marquand divisait un carré en cases égales en fonction du nombre d'articles. La figure 10 montre le diagramme pour 6 thèmes. Le x qui y apparaît indique la classe &AB onsC DEF (ni A, B, ni C, ni D, E, F). Ce type de graphique permet également de résoudre les problèmes de n thèmes, obscurcissant les carrés vides et marquant avec un X ceux des éléments.
Suivant ce type de diagrammes, différentes divisions du carré ont été proposées qui ne sont pas mentionnées ici.
Un autre grand mathématicien et articuliste qui a essayé de représenter le calcul de la proposition par des diagrammes est Martin Gardner lui-même, du livre intitulé “Machines et diagrammes logiques”, dont nous avons tiré l'essence de cet article.
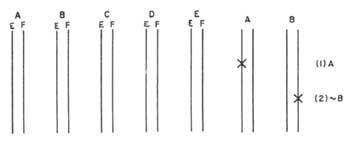
Martin propose un diagramme en réseau. Chaque thème du problème est exprimé par deux droites verticales et parallèles. Chacun indiquera un titre. Par convention le gauche sera vrai et le droit faux. (Figure 3). Si un thème est vrai, un X sera indiqué sur la droite gauche. Si elle est fausse, sur celle de droite. Les énoncés rapportant deux thèmes seront exprimés directement horizontalement, selon le tableau de l'énoncé. Nous appellerons ces ponts directs, car entre deux thèmes jouent le rôle de pont. La figure 4 montre quelques exemples: La figure 4a) montre toutes les droites qui peuvent relier deux thèmes par rapport aux valeurs de la table correspondante. Le pont supérieur indique dans le diagramme 4b) le rapport A B, “A et B”, c'est-à-dire des quatre possibilités on ne peut remplir que la CE. Cependant, le pont inférieur indique la relation A & B, “A et non B”. Dans le diagramme 4d) nous avons l'énoncé A, “A seulement si B”. Le diagramme 4e) montre celui correspondant à l'énoncé A B, “ou A ou B, mais pas tous les deux à la fois”.
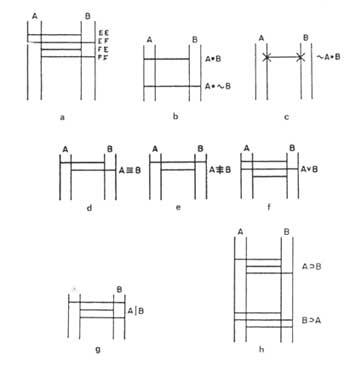
Si dans un énoncé nous avions un seul pont, par exemple &A B, «non A et B», ce serait vrai et nous écririons x aux deux extrémités du pont. Déterminer la valeur des deux questions 4c). A négocier B, “A et B ne sont pas réellement simultanés”, dans le diagramme de l’énoncé (g) apparaissent trois ponts; A, “A et B”, qui manquent de l’énoncé. Nous dirons donc que ces deux énoncés sont niés entre eux. Les énoncés A B « Si A puis B » et B A « si B puis A » apparaissent dans le diagramme de la figure 4h). Ce type d'énoncés n'a pas d'autre signification que celle indiquée dans le calcul de proposition par les ponts du diagramme. Par conséquent, une proposition réelle ne peut impliquer qu'une proposition réelle. Cependant, de fausses propositions peuvent impliquer à la fois la proposition réelle et la fausse proposition.
Nous avons vu toutes les relations binaires entre deux thèmes via des diagrammes en réseau. Deux relations binaires seront équivalentes si dans leurs diagrammes de réseau apparaissent les mêmes ponts.
Voyons le problème proposé par Martin, qui est composé des prémisses suivantes:

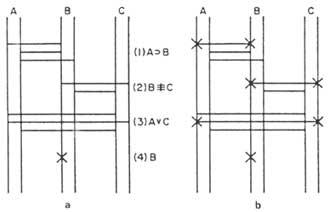
La première étape consiste à représenter le diagramme à quatre prémisses (figure 5 a)). La deuxième étape consiste à explorer la structure de l’échafaudage afin de déterminer si les valeurs des éléments A et C sont parfaitement déterminées : Comme la valeur de B est connue, nous commencerons dans la droite réelle de B. Nous devons chercher un pont qui se termine sur cette droite. Ce pont devra se conformer que depuis la ligne droite de l'autre extrémité on ne peut pas arracher un autre pont qui nous amène à contradiction avec le précédent. Par exemple, deux ponts de 1 prémisse se terminent en direct. Si nous suivons le second, il se dirige vers la fausse ligne droite de A. Par conséquent, nous aurions une contradiction. Si nous choisissons le supérieur, nous arriverions en contradiction, après avoir parcouru un chemin plus long.
Par conséquent, le seul pont qui ne nous contredit pas est de 2 prémisses, nous devons donc passer par lui en écrivant un x aux deux extrémités du pont. Par conséquent, 4 et 2 prémisses nous obligent à dire que c est faux. La fausse droite de C surmonte un seul pont de 3 prémisses. Par conséquent, à cette extrémité du pont, nous écrirons également x. En traversant le pont de 3 lieux, nous arriverons à la droite royale de A, où nous mettrons une autre x. Nous avons obtenu faux C et réel A. Cependant, nous devons suivre l'étude pour nous assurer que nous ne parviendrons pas à la contradiction. La vraie droite de A, et le seul pont qui ne nous contredit arrive à la prémisse 1. Nous avons écrit un x à l'extrémité gauche de ce pont. Si nous traversons le pont, nous arriverons à la vraie droite de B sans trouver de contradictions. Nous y mettrons un autre x, fermant ainsi le parcours. Nous aurons alors la figure 5b).
Si nous voulons analyser d'autres chemins, vous verrez qu'il n'y a pas d'autre possibilité sans contradictions. Nous concluons donc que A est vrai, B est vrai et C faux.
Voici le problème le plus difficile pour vous d'essayer:
1 En Août, ou je porte le chapeau ou je laisse la tête vide.
2 Je ne vais jamais décapité en août si je mets une cravate.
3 En août je porte le chapeau ou la cravate et parfois les deux
Pour faciliter l'examen, nous vous recommandons les sujets suivants:
En août je porte le chapeau
B En août je porte une cravate
C Août en blanc
Des diagrammes d'énoncés composés peuvent également être obtenus. Martin, à titre d'exemple, nous montre dans son livre (A v B) le diagramme de l'énoncé (C v D) (Figure 6a). Les diagrammes des énoncés (A v B) et (C v D) représentent les ponts par parties pour indiquer qu'ils sont provisoires. Si nous savions alors qu'elles sont vraies, nous les représenterions avec une ligne complète. En cas de faux, les ponts manquants pourraient être supprimés et représentés par des lignes complètes (ceux correspondant au refus).
Le rapport d'implication est représenté en dessinant des lignes droites horizontales à côté des diagrammes des énoncés (A v B) et (C v D), deux paires à la hauteur des énoncés. Nous supposons maintenant que la droite inférieure est certaine. Parmi ces quatre droites horizontales nous représenterons les ponts d'implication. Car il n'y a aucun doute sur sa validité.
Si au lieu de A v B nous avions un thème simple, par exemple A, pour exprimer son provisoire, nous mettrons en vraie droite \(moitié de x). S'il s'est avéré faux, nous le supprimerions et marquerons à nouveau dans x. Si cela devenait vrai, nous finirions x.
Dans le diagramme 6b) (B C) apparaît l'énoncé v A).
Nous pourrions représenter une chaîne de sujets liés aux mêmes relations en marquant directement le cercle 0 correspondant aux thèmes qui apparaissent dans la chaîne. Par exemple, le diagramme de la chaîne A & B D peut être vu dans la figure 6c).