Diagrames lògics (II)
En el número de juny es van explicar algunes de les possibilitats del diagrama de Venn. Però aquest no és l'únic sistema inventat. Com veurem a continuació, existeixen altres sistemes per a utilitzar en la lògica de classes i de proposta.
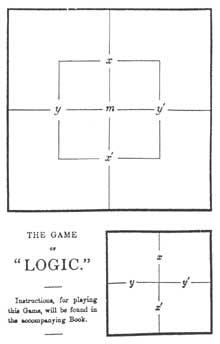
Un altre sistema és l'ideat pel prestigiós escriptor Lewis Carroll. Lewis no es va valer de cercles sinó de quadrats. Les explicarem tal com les usava. Dividia un quadrat en quatre caselles iguals per a incloure totes les combinacions de X e I. Posteriorment, per a l'ús de la tercera matèria incloïa dins d'aquest quadrat altre més petit (Figura 1). Així apareixien totes les combinacions possibles entre X, I i M. Lewis utilitzava X’ (no X) per a expressar la negació del terme X. Així la meitat superior del quadrat és X, la meitat inferior és X’ (no X). La part esquerra és I, la dreta és I, mentre que la part interior del quadrat petit és M l'exterior és M’.
Marcava amb fitxes les regions adequades per a traduir les premisses d'un sil·logisme. Per això, a les regions amb elements posava la fitxa vermella i en les sense elements la fitxa grisa. En les dues regions contigües hi havia elements però en les quals no sabia, posava la fitxa vermella en la línia fronterera.
Podria intentar resoldre el problema típic de Lewis:

Si les fitxes es col·loquen seguint les regles de Lewis, es pot concloure que “cap I és X” és correcta, és a dir, a cap rossinyol el sucre molesta. Els lògics clàssics no acceptarien aquest sil·logisme.
El diagrama de Lewis pot estendre's a n temis. El mateix Lewis ens mostra en el seu llibre Symbolic Logyc un diagrama de 256 caselles adaptades a vuit temes.
El gràfic de Lewis apareix per primera vegada en The Game of Logyc. Juntament amb el fullet es lliurava als compradors una targeta amb el diagrama de Lewis i una bossa amb nou fitxes (quatre vermelles i cinc grisos), tal com es mostra en la figura 1.
El diagrama de Lewis és de la mena de diagrames que va inventar el claustral de la Universitat Alland Marquand John Hopkins amb l'objectiu d'estendre'l a n temis en el diagrama de tres temes.
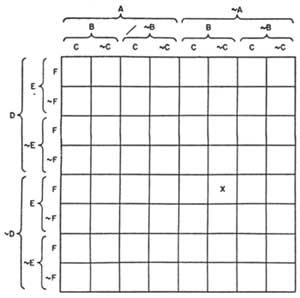
Marquand dividia un quadrat en caselles iguals en funció del nombre d'articles. En la figura 10 es pot veure el diagrama per a 6 temes. La x que apareix en ella indica la classe &AB&C&DEF (ni A, B, ni C, ni D, E, F). Aquest tipus de gràfic també permet resoldre problemes de n temis, enfosquint els quadrats buits i marcant amb una X els d'elements.
Seguint aquest tipus de diagrames s'han proposat diferents divisions del quadrat que no s'esmenten aquí.
Un altre gran matemàtic i articulista que ha tractat de representar el càlcul de la proposta mitjançant diagrames és el mateix Martin Gardner, del llibre titulat “Màquines i diagrames lògics”, l'essència dels quals hem tret d'aquest article.
Martín proposa un diagrama en xarxa. Cada tema del problema s'expressa mitjançant dues rectes verticals i paral·leles. Cadascun indicarà un títol. Per conveni l'esquerre serà veritable i el dret fals. (Figura 3). Si un tema és cert, s'indicarà una X sobre la recta esquerra. Si és falsa, en la de la dreta. Els enunciats que relacionen dos temes els expressarem directament de forma horitzontal, segons el quadre de l'enunciat. A aquests directes els direm ponts, ja que entre dos temes compleixen el paper de pont. En la figura 4 es mostren alguns exemples: En la figura 4a) es mostren tots els rectes que poden unir dos temes enfront dels quals es troben els valors de la taula corresponent. El pont superior indica en el diagrama 4b) la relació A B, “A i B”, és a dir, de les quatre possibilitats només es pot emplenar la CE. No obstant això, el pont inferior indica la relació A B, &“A i no B”. En el diagrama 4d) tenim l'enunciat A, “A només si B”. El diagrama 4e) mostra el corresponent a l'enunciat A B, “o A o B, però no tots dos alhora”.
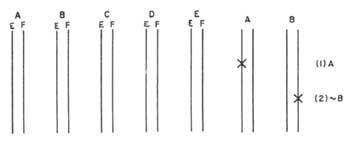
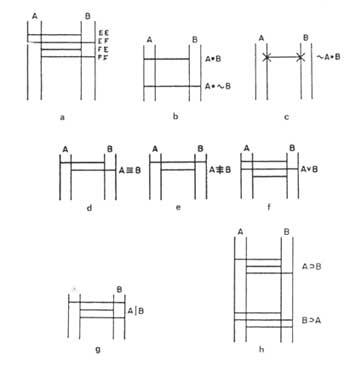
Si en un enunciat tinguéssim un sol pont, per exemple &A B, “no A i B”, seria cert i escriuríem x en els dos extrems del pont. Determinant el valor de totes dues qüestions 4c). A|B, “A i B no són simultanis de debò”, en el diagrama de l'enunciat (g) apareixen tres ponts; A B, “A i B”, que falten a l'enunciat. Per tant, direm que aquests dos enunciats són negats entre si. Els enunciats A B “Si A llavors B” i B A “si B llavors A” apareixen en el diagrama de la figura 4h). Aquest tipus d'enunciats no tenen un altre significat que l'indicat en el càlcul de proposta pels ponts del diagrama. Per tant, una proposició real només pot implicar una proposició real. No obstant això, les proposicions falses poden implicar tant la proposició real com la proposició falsa.
Hem vist totes les relacions binàries entre dos temes mitjançant diagrames en xarxa. Dues relacions binàries seran equivalents si en els seus diagrames de xarxa apareixen els mateixos ponts.
Vegem el problema que proposa Martín, que està compost per les següents premisses:

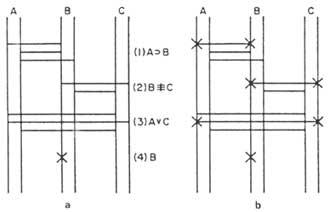
El primer pas consisteix a representar el diagrama de quatre premisses (figura 5 a)). El segon pas consisteix a explorar l'estructura de la “bastida”, a fi de determinar si queden perfectament determinats els valors dels elements A i C: Com el valor de B és conegut, començarem en la recta real de B. Hem de buscar un pont que acaba en aquesta recta. Aquest pont haurà de complir que des de la recta final de l'altre extrem no es pot arrencar un altre pont que ens porti a contradicció amb l'anterior. Per exemple, dos ponts d'1 premissa finalitzen en directe. Si seguim el segon, es dirigeix cap a la recta falsa de A. Per tant, tindríem una contradicció. Si triem el superior, arribaríem a contradicció, després d'haver recorregut un camí més llarg.
Per tant, l'únic pont que no ens contradiu és de 2 premisses, per la qual cosa hem de passar per ell escrivint una x en els dos extrems del pont. Per tant, 4 i 2 premisses ens obliguen a dir que c és falsa. La falsa recta de C remata un únic pont de 3 premisses. Per tant, en aquest extrem del pont també escriurem x. Creuant el pont de 3 premisses, arribarem a la recta real de A, on posarem una altra x. Hem aconseguit fals C i real A. No obstant això, hem de seguir l'estudi per a assegurar que no arribarem a la contradicció. La veritable recta de A, i l'únic pont que no ens contradiu arriba a la premissa 1. Escrivim una x en l'extrem esquerre d'aquest pont. Si creuem el pont arribarem a la veritable recta de B sense trobar contradiccions. En ella col·locarem una altra x, tancant així el recorregut. Tindrem llavors la figura 5b).
Si volem analitzar altres camins, veuràs que no hi ha una altra possibilitat sense contradiccions. Concloem, per tant, que A és veritable, B és veritable i C fals.
Aquí et deixem el problema més difícil perquè l'intentis:
1 A l'agost, o porto el barret o em deixo el cap buit.
2 Mai vaig escapçat a l'agost si em poso corbata.
3 A l'agost porto el barret o la corbata i a vegades els dos
Per a facilitar l'examen et recomanem els següents temes:
A A l'agost porto el barret
B A l'agost porto corbata
C Agost en blanc
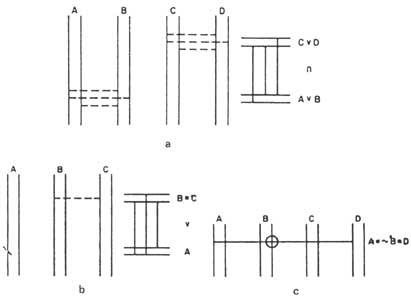
També es poden obtenir diagrames d'enunciats composts. Martin, a tall d'exemple, ens mostra en el seu llibre (A v B) el diagrama de l'enunciat (C v D) (Figura 6a). En els diagrames dels enunciats (A v B) i (C v D) es representen els ponts per parts per a indicar que són provisionals. Si després sabéssim que són certes, les representaríem amb una línia completa. En cas de ser falsos, podrien eliminar-se i representaríem amb línies completes els ponts que falten (els corresponents a la denegació).
La relació d'implicació es representa dibuixant rectes horitzontals al costat dels diagrames dels enunciats (A v B) i (C v D), dos parells a l'altura dels enunciats. Ara suposem que la recta inferior és certa. Entre aquestes quatre rectes horitzontals representarem els ponts d'implicació. Perquè no hi ha dubte de la seva validesa.
Si en lloc de v B tinguéssim un tema simple, per exemple A, per a expressar la seva provisionalitat, posaríem en veritable recta \(meitat de x). Si després resultés fals, ho esborraríem i anotaríem una altra vegada en x. Si tornés a ser cert, acabaríem x.
En el diagrama 6b) (B C) apareix l'enunciat v A).
Podríem representar una cadena de temes relacionats amb les mateixes relacions marcant directament el cercle 0 corresponent als temes que apareixen en la cadena. Per exemple, el diagrama de la cadena A &B D es pot veure en la figura 6c).