Regulation of use of the Chinese abaco (and III). Square and cubic root
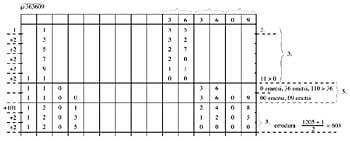
Square root
As you read the solution we just explained, you can see the example.
Resolution
- Placing the sign on the right side of the abacus, and as in the written arithmetic, divide the figures by commas (if there are commas).
- On the left side of the abacus 1 is marked (to the rodura) and the first group on the left of the erroneous is removed.
- Add two to the root (1i) and remove the sum to the previous group. Continue until the bearing is larger than the first group to the left of the erroneous.
- Then a 0 is added to the right column and an 11 is added; in the error two groups are taken and the previous sum is subtracted to the two groups (as if it were one). Now 2 is added to the root and removed to the whole of the rocky sum as in point 3, until the rodura is greater than the whole of the face. Then it repeats what was said at the beginning of this point until the whole number is finished.
- As is often the case, if grouping a new group from the wrong group the grouping is less than the bearing (in our example) another group will gather, but this time to the root (instead of adding a 0 and adding 11) you have to add two zeros and add 101. Then we will continue as in points 3 and 4.
- Once the complete error is completed, we add a rodeo and calculate half of the sum. The result is the roar.
Note:
if it is not an integer, when you take the first group to the right of the comma of the face you put the comma. To finish the operation, add 1 in the first column on the right of the root, regardless of the comma. Then we calculate the semisum and finish.
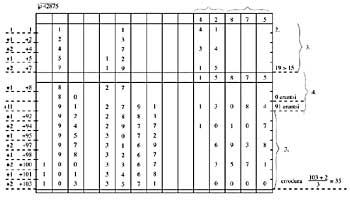
Cubic root
In order to perform this operation, in most cases you will need an abacus of at least 15 columns, or two abacus, or write the roll on paper.
As in the previous case, as the solution is being read, the example is being analyzed.
Resolution
- The plaster will be located on the right side of the abacus and will be divided into groups of three figures starting from the coma of the face.
- On the left side of the abacus 1 (rodura) is placed and the first group is removed to the left of it. Mark in the center of abacus 1 (intermediate rolling).
- Add to the root, 1i, one and add the addition to the intermediate root (3). Add to the root, 2ri, 2 and add the addition to the intermediate root (7). Remove the first intermediate tread group.
Repeat all of the above until the intermediate bearing is larger than the first radical group. - The next group meets. Add 1 to the root and add to the intermediate root. Add a 0 to the footprint in the right column and add 11. Add this sum to the intermediate error in the two columns on the right. The new intermediate bearing must be removed from the first two groups of the wrong one. It
will then follow as in points 3 and 4. - If once the next group was assembled the intermediate bearing was too large, another group would be taken, but instead of adding 0 and adding 11, we would add two zeros and add 101. The total sum would be added to the intermediate rodeo in the four columns on the right. We would follow the above in points 3 and 4.
- Once the integer is completed, the cubic root will be added 2 to the root and will be a third of the sum.
Note:
in the event that the comma has a comma, it will be placed when the first group is taken from the right of the comma of the comma of the comb in the root. In the end, the 2 that must be added to calculate the bearing is added to the roll without taking into account the comma in the right column.

With this we end the issue of the figures (for the moment). In short, the history of the figures has fulfilled five articles in numbers 34, 35, 36, 37-38 and 39, how do they operate? Article 40 and 41 and finally Abacus: history and use in numbers 42, 43 and 44.