Hasiera »   Erreportajeak »   2006ko Abel saria: analista baten indarra

Premio Abel 2006: A forza dun analista

• Zabaldu:
• Twitter
• Facebook
• Emaila

O premio Abel foi outorgado por cuarta vez este ano, o máximo premio mundial que un matemático pode gañar. O gañador foi o sueco Lennart Carleson, un matemático de recoñecido prestixio no campo da análise matemática. O xurado destacou a forza que exerceu paira abordar e resolver problemas difíciles, e especialmente a pegada que deixou en dous ámbitos: Teoría de series de Fourie e sistemas dinámicos.

En 1902 aparecen tres intencións de Niels Henri paira conmemorar o primeiro centenario do nacemento de Abel e difundir o seu prestixio: celebrar actos culturais, establecer una estatua e organizar un premio internacional. Celebráronse actos culturais, o Estado inaugurouse en 1908, pero o premio non se organizou. Parece que estiveron a piques de facelo, pero cando en 1905 Noruega separouse de Suecia, alí foron os soños de crear o premio.

A piques de cumprirse o segundo centenario, recuperouse a idea centenaria e pediuse ao goberno noruegués que crease un premio. En 2002 o goberno noruegués aprobou os estatutos do Fondo Abel. O obxectivo principal do fondo é "Outorgar un premio internacional a un traballo científico relevante no campo das matemáticas". Parece que este premio pode estar no camiño de ser un substituto do que podería ser o Nobel de Matemáticas: onde se emite --Noruegués--, quen --os reis noruegueses ou raíña de Noruega -, canto diñeiro -case, entre outros -. O futuro dirá si é así ou non, segundo vaian cumprindo os anos.

Lennart Carlos

O premio Abel 2006 foi paira Lennart Carles, matemático destacado na análise clásica. Nacido en Estocolmo en 1928, estudou na Universidade de Uppsala, onde presentou a súa tese doutoral en 1950. As matemáticas, sobre todo a análise, tiveron una gran tradición en Suecia, XIX. A partir da segunda metade do século XX. O propio director de Carleson, Arne Beurling, é un destacado analista.

Con 25 anos conseguiu o posto de profesor da Universidade de Estocolmo, pero pronto regresou a Uppsala. Alí foi profesor até 1993; anos despois, sen deixar de traballar, foi tamén profesor da Universidade UCLA de Los Ángeles.

Entre os traballos de Carleson destacan a resposta que deu a problemas difíciles que estiveron pendentes de resolución durante varios anos. Por exemplo, en 1962 demostrou o teorema da Coroa e, así, o matemático xaponés Kakutani resolveu a pregunta que lanzara vinte anos antes.

Foi maior o que fixo catro anos despois, ao resolver o maior problema aberto da teoría de series de Fourie, a converxencia punto a punto. Con iso entrou na historia das Matemáticas.

Ademais, na década dos 80, fronte á crenza de que os matemáticos obteñen os seus principais resultados a idades temperás, deu resposta a un problema aberto en sistemas dinámicos suaves, xunto a Michael Benedicks.

Ademais de todo isto, é evidente o traballo de Carlesón polas Matemáticas. Velaquí un exemplo. En 1916 o matrimonio Mittag-Leffler declarou a súa intención de deixar a súa casa e a súa biblioteca á Academia Sueca de Ciencias paira crear un instituto de matemáticas. En 1927 morreu Mittag-Leffler, o instituto fundouse, pero non se organizou por falta de diñeiro segundo as súas intencións. En 1967 o Goberno sueco deu a oportunidade a Carleson de traballar onde quería e el decidiu pór en marcha o instituto Mittag-Leffler. Tamén o fixo, obtivo as subvencións necesarias e converteuno nun dos centros de investigación máis prestixiosos do mundo. Até 1984 foi director do instituto.

Series Fourie

As series de Fourie están a piques de cumprir os douscentos anos. De feito, é de 1807 cando Joseph Fourier presentou o seu primeiro traballo á Academia da Ciencia de París. Propuxo e resolveu a ecuación da propagación da calor, inventando paira iso una vía específica, a distribución de variables que resultou tan útil. A función que dá a temperatura inicial escríbese como serie de seo e coseno, é dicir, como suma infinita, e Fourier afirmou que isto é posible paira todas as funcións.

Confirmar si, probar non. Non é de estrañar que até entón desenvolveu enormemente as análises matemáticas

ferramentas de cálculo, pero non “medios de proba xeométricos”, en palabras de Cauchy. Como o novo vento do rigor requiría probas, a afirmación de Fourie non era un teorema, pero se converteu nun problema. E moi importante, o XIX. Na xénese e evolución de moitos dos conceptos da análise matemática do século XX foron series trigonométricas: función, integral, converxencia uniforme...

XIX. A teoría clásica das series de Fourie acababa co século XIX. XX. Nos primeiros anos do século XX, con todo, o sector foi completamente renovado. As razóns foron dúas: Teoría da medida e integral de Lebesgue e teoría dos espazos funcionais, é dicir, análise funcional actual.

O aiero de Lusin chegou en 1913: se o cadrado dunha función é integrable, a súa serie de Fourie coincide en todos os puntos, excepto nun “conxunto de lonxitude cero”. A afirmación débese ao matemático ruso Lusin, non probada, pero si coa convicción de ser un teorema.

Co paso dos anos reuníronse outros teoremas no campo das series de Fourie, pero ninguén daba esa categoría á conxectura de Lusin. Nin ao contrario, porque iso tamén podía ocorrer. A verdade é que, a partir dun momento, entre os expertos empezou a xeneralizarse esa convicción de que a intuición de Lusin estivo equivocada. Por iso, cando en 1965 Carleson demostrou o teorema, foi en certa medida una sorpresa.

El mesmo contou que durante varios anos tentou demostrar o contrario. Cando pensaba que tiña todas as ferramentas dispoñibles paira un contraposición, resultoulle imposible. Entón viu que tiña que tomar a outra vía, a de si, e puido conseguir o resultado coas ferramentas acumuladas.

A proba de Carleson tivo desde o principio a fama de ser misterioso. Aínda que tecnicamente era correcto, non se entendía. Aínda parece que as causas da súa estrutura interna son demasiado inclinadas paira a maioría. Paira utilizar a comparación do matemático Michael Christ é como a ascensión dun monte de oito mil metros, a maioría non somos capaces de camiñar pola nosa conta, pero Carlesón demostrounos que hai un camiño que leva á cima.

Sistemas dinámicos

Tamén noutro campo das matemáticas, Carleson fixo camiños á cima, por exemplo, en sistemas dinámicos.

Tomar una función do plano ao plano, por exemplo, e aplicar a función varias veces comezando nun punto. Cal é o comportamento da sucesión de puntos obtida --orbital -? Achégase a un límite, vai ao infinito ou fai algo máis? A partir desta pregunta e dependendo das funcións, xurdiu un campo das Matemáticas. A finais do século XX, sobre todo da man do matemático francés Henri Poincaré.

Tras uns resultados teóricos, a verdadeira innovación no campo produciuse no computador. Facendo ver as órbitas dos puntos na pantalla podíase sospeitar do que podía pasar, paira facer conxecturas. Logo terían que vir as probas. De aí xurdiu o que chamaron a teoría do Caos.

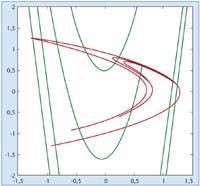
É frecuente citar un estudo do meteorólogo Lorentz como uno dos primeiros exemplos do caos. En 1976 outro meteorólogo, Michel Hénon, resumindo as ecuacións de Lorentz, deu un sistema de plano no que aparece un comportamento bastante particular. Detéctase un conxunto 'raro', no que as órbitas se dirixen cara alí (aproxímanse ao conxunto pero non a un valor concreto), pero si comezamos nun punto do conxunto obtense una órbita que se despraza no mesmo. E non só iso, a estrutura do conxunto é rara, xa que é fractal. Por iso inventouse o termo "estraña atracción". É posible demostralo matematicamente?

Na década dos 80 entrou en Carles no campo dos sistemas dinámicos. Xunto a Michael Benedicks, inventou un novo método paira estudar un primeiro caso sinxelo. Posteriormente, adaptaron o método paira poder aplicalo ao sistema de Hénon e foron capaces de describir a súa dinámica, convertendo a conxectura de anos anteriores nun teorema. Con estes resultados, o artigo publicado por Carlos e Benedicks en 1992 quedou como un fito na teoría dos sistemas dinámicos.