Premi Abel 2006: La força d'un analista

A punt de complir-se el segon centenari, es va recuperar la idea centenària i es va demanar al govern noruec que creés un premi. En 2002 el govern noruec va aprovar els estatuts del Fons Abel. L'objectiu principal del fons és "Atorgar un premi internacional a un treball científic rellevant en el camp de les matemàtiques". Sembla que aquest premi pot estar en el camí de ser un substitut del que podria ser el Nobel de Matemàtiques: on s'emet --Noruec--, qui --els reis noruecs o reina de Noruega -, quants diners -gairebé, entre altres -. El futur dirà si és així o no, segons vagin complint els anys.
Lennart Carlos
El premi Abel 2006 ha estat per a Lennart Carles, matemàtic destacat en l'anàlisi clàssica. Nascut a Estocolm en 1928, va estudiar en la Universitat d'Uppsala, on va presentar la seva tesi doctoral en 1950. Les matemàtiques, sobretot l'anàlisi, han tingut una gran tradició a Suècia, XIX. A partir de la segona meitat del segle XX. El propi director de Carleson, Arne Beurling, és un destacat analista.

Amb 25 anys va aconseguir el lloc de professor de la Universitat d'Estocolm, però aviat va tornar a Uppsala. Allí va ser professor fins a 1993; anys després, sense deixar de treballar, va anar també professor de la Universitat UCLA de Los Angeles.
Entre els treballs de Carleson destaquen la resposta que ha donat a problemes difícils que han estat pendents de resolució durant diversos anys. Per exemple, en 1962 va demostrar el teorema de la Corona i, així, el matemàtic japonès Kakutani va resoldre la pregunta que havia llançat vint anys abans.
Va ser major el que va fer quatre anys després, en resoldre el major problema obert de la teoria de sèries de Fourie, la convergència punt a punt. Amb això va entrar en la història de les Matemàtiques.
A més, en la dècada dels 80, enfront de la creença que els matemàtics obtenen els seus principals resultats a edats primerenques, va donar resposta a un problema obert en sistemes dinàmics suaus, al costat de Michael Benedicks.
A més de tot això, és evident el treball de Carlesón per les Matemàtiques. Heus aquí un exemple. En 1916 el matrimoni Mittag-Leffler va declarar la seva intenció de deixar la seva casa i la seva biblioteca a l'Acadèmia Sueca de Ciències per a crear un institut de matemàtiques. En 1927 va morir Mittag-Leffler, l'institut es va fundar, però no es va organitzar per falta de diners segons les seves intencions. En 1967 el Govern suec va donar l'oportunitat a Carleson de treballar on volia i ell va decidir posar en marxa l'institut Mittag-Leffler. També ho va fer, va obtenir les subvencions necessàries i ho va convertir en un dels centres de recerca més prestigiosos del món. Fins a 1984 va ser director de l'institut.
Sèries Fourie
Confirmar sí, provar no. No és d'estranyar que fins llavors va desenvolupar enormement les anàlisis matemàtiques
eines de càlcul, però no “mitjans de prova geomètrics”, en paraules de Cauchy. Com el nou vent del rigor requeria proves, l'afirmació de Fourie no era un teorema, però es va convertir en un problema. I molt important, el XIX. En la gènesi i evolució de molts dels conceptes de l'anàlisi matemàtica del segle XX van ser sèries trigonomètriques: funció, integral, convergència uniforme...

XIX. La teoria clàssica de les sèries de Fourie acabava amb el segle XIX. XX. En els primers anys del segle XX, no obstant això, el sector va ser completament renovat. Les raons van ser dues: Teoria de la mesura i integral de Lebesgue i teoria dels espais funcionals, és a dir, anàlisi funcional actual.
L'aiero de Lusin va arribar en 1913: si el quadrat d'una funció és integrable, la seva sèrie de Fourie coincideix en tots els punts, excepte en un “conjunt de longitud zero”. L'afirmació es deu al matemàtic rus Lusin, no provada, però sí amb la convicció de ser un teorema.
Amb el pas dels anys es van reunir altres teoremes en el camp de les sèries de Fourie, però ningú donava aquesta categoria a la conjectura de Lusin. Ni al contrari, perquè això també podia ocórrer. La veritat és que, a partir d'un moment, entre els experts va començar a generalitzar-se aquesta convicció que la intuïció de Lusin va estar equivocada. Per això, quan en 1965 Carleson va demostrar el teorema, va anar en certa manera una sorpresa.
Ell mateix ha contat que durant diversos anys va intentar demostrar el contrari. Quan pensava que tenia totes les eines disponibles per a un contraposició, li va resultar impossible. Llavors va veure que havia de prendre l'altra via, la de si, i va poder aconseguir el resultat amb les eines acumulades.
La prova de Carleson va tenir des del principi la fama de ser misteriós. Encara que tècnicament era correcte, no s'entenia. Encara sembla que les causes de la seva estructura interna són massa inclinades per a la majoria. Per a utilitzar la comparació del matemàtic Michael Christ és com l'ascensió d'una muntanya de vuit mil metres, la majoria no som capaces de caminar pel nostre compte, però Carlesón ens va demostrar que hi ha un camí que porta al cim.
Sistemes dinàmics
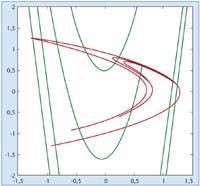
Prendre una funció del pla al pla, per exemple, i aplicar la funció diverses vegades començant en un punt. Quin és el comportament de la successió de punts obtinguda --orbital -? S'acosta a un límit, va a l'infinit o fa alguna cosa més? A partir d'aquesta pregunta i depenent de les funcions, va sorgir un camp de les Matemàtiques. A la fi del segle XX, sobretot de la mà del matemàtic francès Henri Poincaré.
Després d'uns resultats teòrics, la veritable innovació en el camp es va produir en l'ordinador. Fent veure les òrbites dels punts en la pantalla es podia sospitar del que podia passar, per a fer conjectures. Després haurien de venir les proves. D'aquí va sorgir el que han anomenat la teoria del Caos.

És freqüent citar un estudi del meteoròleg Lorentz com un dels primers exemples del caos. En 1976 un altre meteoròleg, Michel Hénon, resumint les equacions de Lorentz, va donar un sistema de pla en el qual apareix un comportament bastant particular. Es detecta un conjunt 'estrany', en el qual les òrbites es dirigeixen cap a allí (s'aproximen al conjunt però no a un valor concret), però si comencem en un punt del conjunt s'obté una òrbita que es desplaça en aquest. I no sols això, l'estructura del conjunt és estranya, ja que és fractal. Per això es va inventar el terme "estranya atracció". És possible demostrar-ho matemàticament?
En la dècada dels 80 va entrar en Carles en el camp dels sistemes dinàmics. Al costat de Michael Benedicks, va inventar un nou mètode per a estudiar un primer cas senzill. Posteriorment, van adaptar el mètode per a poder aplicar-lo al sistema d'Hénon i van ser capaços de descriure la seva dinàmica, convertint la conjectura d'anys anteriors en un teorema. Amb aquests resultats, l'article publicat per Carlos i Benedicks en 1992 ha quedat com una fita en la teoria dels sistemes dinàmics.






