Hasiera »   Erreportajeak »   2006ko Abel saria: analista baten indarra

Abel Prize 2006: The strength of an analyst

• Zabaldu:
• Twitter
• Facebook
• Emaila

The Abel prize has been awarded for the fourth time this year, the world's highest prize a mathematician can win. The winner was Swedish mathematician Lennart Carleson, a renowned mathematician in the field of mathematical analysis. The jury highlighted the strength it has exercised to address and solve difficult problems, and especially the footprint it has left in two areas: Fourie series theory and dynamic systems.

In 1902 there were three intentions of Niels Henri to commemorate the first centenary of the birth of Abel and to spread his prestige: to celebrate cultural events, to establish a statue and to organize an international prize. Cultural events were held, the State was inaugurated in 1908, but the prize was not organized. It seems they were about to do so, but when in 1905 Norway separated from Sweden, there were dreams of creating the prize.

At the end of the second centenary, the centennial idea was recovered and the Norwegian government was asked to create an award. In 2002 the Norwegian government approved the statutes of the Abel Fund. The main objective of the fund is "To award an international prize for relevant scientific work in the field of mathematics". It seems that this prize may be on the path of being a substitute for what might be the Nobel Prize in Mathematics: where it is issued --Norwegians--, who --the Norwegian kings or queen of Norway -, how much money -almost, among others -. The future will say whether it is so or not, as the years go by.

Lennart Carlos

The 2006 Abel prize went to Lennart Carles, a mathematician outstanding in classical analysis. Born in Stockholm in 1928, he studied at the University of Uppsala, where he presented his doctoral thesis in 1950. Mathematics, especially analysis, has had a great tradition in Sweden, XIX. From the second half of the twentieth century. Carleson's own director, Arne Beurling, is a leading analyst.

At the age of 25 he became professor at the University of Stockholm, but soon returned to Uppsala. There he was professor until 1993; years later, while still working, he was also professor at UCLA University in Los Angeles.

Carleson's work highlights the response it has given to difficult problems that have been pending resolution for several years. For example, in 1962 he demonstrated the Crown theorem and thus the Japanese mathematician Kakutani solved the question he had launched twenty years earlier.

It was greater than he did four years later, by solving the biggest open problem of Fourie series theory, point-to-point convergence. He thus entered the history of mathematics.

In addition, in the 1980s, faced with the belief that mathematicians obtain their main results at an early age, it responded to an open problem in soft dynamic systems, along with Michael Benedicks.

In addition to all this, Carlesón's work for mathematics is evident. Here is an example. In 1916 the marriage Mittag-Leffler declared his intention to leave his house and his library to the Swedish Academy of Sciences to create a mathematics institute. In 1927 Mittag-Leffler died, the institute was founded, but it was not organized for lack of money according to his intentions. In 1967 the Swedish government gave Carleson the opportunity to work where he wanted and he decided to start the Mittag-Leffler institute. He also did, obtained the necessary grants and made it one of the most prestigious research centers in the world. Until 1984 he was director of the institute.

Fourie series

The Fourie series are about to turn two hundred years old. In fact, it was in 1807 that Joseph Fourier presented his first work to the Paris Academy of Science. He proposed and resolved the heat propagation equation, inventing for it a specific pathway, the distribution of variables that has been so useful. The function that gives the initial temperature is written as a sinus and cosine series, that is, as an infinite sum, and Fourier stated that this is possible for all functions.

Confirm yes, try no. No wonder that until then he developed mathematical analyses enormously

calculation tools, but not “geometric test means”, in Cauchy’s words. As the new wind of rigor required evidence, Fourie's claim was not a theorem, but it became a problem. And very important, the XIX. In the genesis and evolution of many of the concepts of mathematical analysis of the twentieth century were trigonometric series: function, integral, uniform convergence...

XIX. The classical theory of the Fourie series ended in the 19th century. XX. In the early years of the 20th century, however, the sector was completely renovated. The reasons were two: Lebesgue measurement theory and integral theory of functional spaces, that is, current functional analysis.

Lusin’s aiero arrived in 1913: if the square of a function is integrable, its Fourie series matches at all points, except in a “zero length set”. The claim is due to the Russian mathematician Lusin, not proven, but with the conviction of being a theorem.

Over the years other theorems gathered in the field of the Fourie series, but no one gave that category to Lusin's conjecture. On the contrary, because that could also happen. The truth is that, from a moment on, among the experts began to generalize that conviction that Lusin's intuition was wrong. Therefore, when Carleson demonstrated theorem in 1965, it was somewhat of a surprise.

He himself has said that for several years he tried to prove otherwise. When he thought he had all the tools available for a counterposition, it was impossible. Then he saw that he had to take the other way, that of himself, and he could get the result with the accumulated tools.

The proof of Carleson had from the beginning the fame of being mysterious. Although technically correct, it was not understood. It still seems that the causes of its internal structure are too inclined for most. To use the comparison of the mathematician Michael Christ is like the ascension of an eight-thousand-meter mountain, most of us are not able to walk on our own, but Carleson showed us that there is a path that leads to the top.

Dynamic systems

Also in another field of mathematics, Carleson made roads to the top, for example, in dynamic systems.

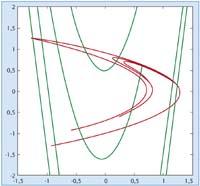
Take a function from plane to plane, for example, and apply the function several times starting at a point. What is the behavior of the succession of points obtained --orbital -? Do you approach a limit, go to infinity or do something else? From this question and depending on the functions, a field of Mathematics emerged. At the end of the 20th century, especially by the hand of the French mathematician Henri Poincaré.

After theoretical results, true innovation in the field occurred on the computer. By showing the orbits of the dots on the screen you could suspect what could happen, to make conjectures. Then the tests would have to come. Hence came what they have called the Chaos theory.

It is common to cite a study by meteorologist Lorentz as one of the first examples of chaos. In 1976 another meteorologist, Michel Hénon, summarizing the equations of Lorentz, gave a plane system in which a quite particular behavior appears. A 'rare' set is detected, in which the orbits are directed there (they approach the set but not a specific value), but if we start at a point of the set an orbit is obtained that moves in it. And not only that, the structure of the whole is rare, as it is fractal. That is why the term "strange attraction" was invented. Is it possible to demonstrate it mathematically?

In the 1980s he entered Carles in the field of dynamic systems. Together with Michael Benedicks, he invented a new method to study a simple first case. Subsequently, they adapted the method to be able to apply it to the Hénon system and were able to describe its dynamics, turning the conjecture of previous years into a theorem. With these results, the article published by Carlos and Benedicks in 1992 has remained a milestone in the theory of dynamic systems.