Hasiera »   Erreportajeak »   2006ko Abel saria: analista baten indarra

Prix Abel 2006: La force d’un analyste

• Zabaldu:
• Twitter
• Facebook
• Emaila

Le prix Abel a été décerné pour la quatrième fois cette année, le plus grand prix mondial qu'un mathématicien peut gagner. Le gagnant a été le suédois Lennart Carleson, un mathématicien de prestige reconnu dans le domaine de l'analyse mathématique. Le jury a souligné la force qu'il a exercée pour aborder et résoudre des problèmes difficiles, et en particulier l'empreinte qu'il a laissée dans deux domaines: Théorie des séries de Fourie et systèmes dynamiques.

En 1902 apparaissent trois intentions de Niels Henri pour commémorer le premier centenaire de la naissance d'Abel et diffuser son prestige : célébrer des actes culturels, établir une statue et organiser un prix international. Des événements culturels ont eu lieu, l'État a été inauguré en 1908, mais le prix n'a pas été organisé. Il semble qu'ils étaient sur le point de le faire, mais quand en 1905 la Norvège s'est séparée de la Suède, il y avait les rêves de créer le prix.

A l'approche du deuxième centenaire, l'idée centenaire a été récupérée et le gouvernement norvégien a été invité à créer un prix. En 2002, le gouvernement norvégien a adopté les statuts du Fonds Abel. L'objectif principal du fonds est "Décerner un prix international à un travail scientifique pertinent dans le domaine des mathématiques". Il semble que ce prix peut être sur le chemin d'être un substitut à ce qui pourrait être le Nobel de Mathématiques: où il est émis --Norvégien -, qui - les rois norvégiens ou reine de Norvège -, combien d'argent - presque, entre autres -. L'avenir dira si oui ou non, au fil des ans.

Lennart Carlos

Le prix Abel 2006 a été pour Lennart Carles, un mathématicien de premier plan dans l'analyse classique. Né à Stockholm en 1928, il a étudié à l'Université d'Uppsala où il a présenté sa thèse de doctorat en 1950. Les mathématiques, en particulier l'analyse, ont eu une grande tradition en Suède, XIX. De la seconde moitié du XXe siècle. Le directeur de Carleson, Arne Beurling, est un éminent analyste.

À 25 ans, il a obtenu le poste de professeur à l'Université de Stockholm, mais il est rapidement retourné à Uppsala. Il a été professeur jusqu'en 1993; années plus tard, tout en continuant à travailler, il a également été professeur à l'Université UCLA de Los Angeles.

Parmi les travaux de Carleson soulignent la réponse qui a donné des problèmes difficiles qui ont été en cours de résolution pendant plusieurs années. Par exemple, en 1962, il a démontré le théorème de la Couronne et, ainsi, le mathématicien japonais Kakutani résolu la question qu'il avait lancé vingt ans plus tôt.

Il a été plus grand ce qu'il a fait quatre ans plus tard, en résolvant le plus grand problème ouvert de la théorie des séries de Fourie, convergence point à point. Ainsi, il est entré dans l'histoire des mathématiques.

En outre, dans les années 80, face à la croyance que les mathématiciens obtiennent leurs principaux résultats à un âge précoce, a donné une réponse à un problème ouvert dans les systèmes dynamiques douces, avec Michael Benedicks.

En plus de tout cela, il est évident le travail de Carleson pour les mathématiques. Voici un exemple. En 1916, le mariage Mittag-Leffler a déclaré son intention de quitter sa maison et sa bibliothèque à l'Académie suédoise des sciences pour créer un institut de mathématiques. En 1927 est décédé Mittag-Leffler, l'institut a été fondé, mais il n'a pas été organisé par manque d'argent selon ses intentions. En 1967, le gouvernement suédois a donné l'occasion à Carleson de travailler où il voulait et il a décidé de lancer l'institut Mittag-Leffler. Il a également obtenu les subventions nécessaires et en a fait l'un des centres de recherche les plus prestigieux au monde. Jusqu'en 1984, il fut directeur de l'institut.

Séries Fourie

Les séries de Fourie sont sur le point d'atteindre les deux cents ans. En fait, il est de 1807 lorsque Joseph Fourier présenté son premier travail à l'Académie des sciences de Paris. Il a proposé et résolu l'équation de la propagation de la chaleur, inventant pour cela une voie spécifique, la distribution de variables qui a été si utile. La fonction qui donne la température initiale est écrit comme une série de sinus et cosinus, à savoir, comme une somme infinie, et Fourier a affirmé que cela est possible pour toutes les fonctions.

Confirmer oui, essayer non. Il n'est pas surprenant que jusqu'alors il a énormément développé les analyses mathématiques

outils de calcul, mais pas “géométriques de test”, dans les mots de Cauchy. Comme le nouveau vent de rigueur nécessitait des preuves, l'affirmation de Fourie n'était pas un théorème, mais il est devenu un problème. Et très important, le XIX. Dans la genèse et l'évolution de plusieurs des concepts de l'analyse mathématique du XXe siècle étaient des séries trigonométriques: fonction, intégrale, convergence uniforme...

XIX. La théorie classique des séries de Fourie se terminait par le 19ème siècle. XX. Dans les premières années du XXe siècle, cependant, le secteur a été entièrement rénové. Les raisons étaient deux: Théorie de la mesure et intégrante de Lebesgue et la théorie des espaces fonctionnels, à savoir l'analyse fonctionnelle actuelle.

L'aérus de Lusin est arrivé en 1913 : si le carré d'une fonction est intégrable, sa série de Fourie coïncide sur tous les points, sauf dans un « ensemble de longueur zéro ». L'affirmation est due au mathématicien russe Lusin, non prouvé, mais avec la conviction d'être un théorème.

Au fil des ans, d'autres théorèmes se réunirent dans le domaine des séries de Fourie, mais personne ne donnait cette catégorie à la conjecture de Lusin. Ni au contraire, parce que cela pouvait aussi se produire. La vérité est que, à partir d'un moment, parmi les experts a commencé à se généraliser cette conviction que l'intuition de Lusin a tort. Ainsi, quand en 1965 Carleson a montré le théorème, il était dans une certaine mesure une surprise.

Il a raconté lui-même que pendant plusieurs années il a essayé de prouver le contraire. Quand il pensait qu'il avait tous les outils disponibles pour une opposition, il s'est avéré impossible. Puis il a vu qu'il devait prendre l'autre voie, celle de lui-même, et a pu obtenir le résultat avec les outils accumulés.

La preuve de Carleson a eu dès le début la réputation d'être mystérieux. Bien que techniquement correct, il n'était pas compris. Il semble encore que les causes de sa structure interne sont trop inclinées pour la plupart. Pour utiliser la comparaison du mathématicien Michael Christ est comme l'ascension d'un mont de huit mille mètres, la plupart ne sont pas en mesure de marcher sur notre propre, mais Carleson nous a montré qu'il ya un chemin menant au sommet.

Systèmes dynamiques

Toujours dans un autre domaine des mathématiques, Carleson a fait des routes vers le haut, par exemple, dans les systèmes dynamiques.

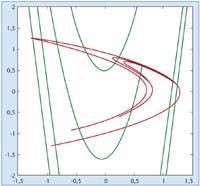
Prendre une fonction du plan au plan, par exemple, et appliquer la fonction plusieurs fois en commençant à un point. Quel est le comportement de la succession de points obtenue --orbital -? Approchez-vous d'une limite, allez à l'infini ou faites-vous autre chose? A partir de cette question et selon les fonctions, un champ de mathématiques a émergé. À la fin du XXe siècle, surtout de la main du mathématicien français Henri Poincaré.

Après des résultats théoriques, la véritable innovation dans le domaine s'est produite sur l'ordinateur. En faisant voir les orbites des points sur l'écran, on pouvait soupçonner de ce qui pouvait arriver, pour faire des conjectures. Ensuite, les épreuves devraient venir. D'où est née ce qu'ils ont appelé la théorie du chaos.

Il est fréquent de citer une étude du météorologue Lorentz comme l'un des premiers exemples du chaos. En 1976, un autre météorologue, Michel Hénon, résumant les équations de Lorentz, donna un système de plan dans lequel apparaît un comportement assez particulier. Un ensemble 'rare' est détecté, dans lequel les orbites s'y dirigent (elles s'approchent de l'ensemble mais pas d'une valeur concrète), mais si on commence à un point de l'ensemble on obtient une orbite qui se déplace dans l'ensemble. Et non seulement cela, la structure de l'ensemble est rare, car elle est fractale. C'est pourquoi le terme "étrange attraction" a été inventé. Est-il possible de le prouver mathématiquement?

Dans les années 80 est entré Carles dans le domaine des systèmes dynamiques. Avec Michael Benedicks, il a inventé une nouvelle méthode pour étudier un premier cas simple. Par la suite, ils ont adapté la méthode pour l'appliquer au système de Hénon et ont pu décrire sa dynamique, convertissant la conjecture des années précédentes en un théorème. Avec ces résultats, l'article publié par Carlos et Benedicks en 1992 est devenu un jalon dans la théorie des systèmes dynamiques.