Una fábula de métodos numéricos: ... e paira comer, ondas de alta frecuencia
Métodos numéricos
As ecuacións diferenciais tiveron una gran importancia. Alí estaban cando había que estudar una nova oportunidade de negocio en calquera empresa, mesmo cando, aplicando uns tipos de interese, queríase saber a cantidade de diñeiro que existise nos bancos ao cabo duns anos, ou entre os enxeñeiros dunha construtora, cando estaban a estudar as vibracións que podía soportar a nova ponte que se estaba construíndo no pobo veciño, ou nun laboratorio de química cando se ía a calcular a dispersión de temperatura dunha superficie... Todas elas levaron a diversas empresas e centros de investigación a identificar e definir a necesidade dun novo posto de traballo, o correspondente ao método numérico. O seu traballo era resolver analiticamente, é dicir, liberar ecuacións diferenciais que non podían ser resoltas ou que non interesaban resolver exactamente. Paira iso, coas operacións necesarias, obtiñan una aproximación ao resultado da ecuación diferencial.
Cando nalgún lugar destas características había que contratar un método numérico, púñase un anuncio en prensa, do mesmo xeito que en calquera outro posto de traballo. E así o fixo tamén o responsable de persoal que estaba a realizar a entrevista nese momento: "Una importante empresa da contorna de Bilbao dedicada á construción de edificios necesita un método numérico. Debe ser capaz de liberar ecuacións diferenciais en ordes baixas e pouco influenciadas por perturbacións ou problemas derivados do medio. Valorarase experiencia na resolución de problemas relacionados con vibracións. O gusto polas ondas de alta frecuencia é fundamental. Ofrece un bo soldo e a posibilidade de utilizar o ximnasio da empresa."
Analizábanse os currículos dos candidatos recibidos paira o posto. O método numérico tiña en conta as capacidades intelectuais e psicolóxicas. Entre os intelectuais tíñase en conta a precisión coa que o método podía resolver a ecuación diferencial. "Fun deseñado e programado paira resolver problemas con precisión en distintas ordes", afirmaba un que paira o resultado aproximado buscado a empresa podía resolver as ecuacións diferenciais coa precisión (grande ou pequena) desexada. Outros só traballaban en primeiro ou segunda orde, é dicir, en ordes baixas e por tanto con pouca precisión. Cando o proxecto que tiña en mans a empresa necesitaba maior precisión, non se contrataban os que liberaban en baixas ordes. Isto non significaba que non existisen empresas paira a contratación de traballadores que traballaban por estas ordes, que noutras podían ser contratados, por suposto.
En canto ás capacidades psicolóxicas, a empresa contratante desexaba coñecer o campo de estabilidade do método numérico. Isto determinaba a resposta do método ante erros ou perturbacións que se producían ao liberar as ecuacións. O método tamén reflectía a súa capacidade de familiarizarse coas peculiaridades da ecuación diferencial --autovalores -. O feito de que o método tivese un campo de estabilidade amplo indicaba que tiña capacidade de actuar ante problemas diversos. Unha área de estabilidade máis pequena, con todo, podía demostrar que ante certas perturbacións o método non daría resultados satisfactorios. Nestes casos, as perturbacións nos problemas resoltos fóra da zona de estabilidade aumentaban e o resultado calculado podía chegar a ser menos bo ou malo.
Canto cobras? "Por custo computacional". O que era capaz de traballar en ordes altas e de evitar perturbacións era custoso. Así, o traballo de varios matemáticos centrábase no deseño destes métodos.
Radio espectral
Con todo, había algunha característica que se ocultaba máis polo método numérico. Una das características ocultas era a denominada amortiguación algorítmica. O que mostraba o comportamento do método con ondas de alta frecuencia.

Existían métodos numéricos de orde alta e estable pero que non tiñan bo comportamento con ondas de alta frecuencia. Isto significaba que cando estabamos a liberar as ecuacións diferenciais nas que aparecían altas frecuencias había métodos que tendían a abusar das altas frecuencias. Nas ecuacións diferenciais en forma de onda, se teoricamente a onda estaba a vibrar nun intervalo de tempo, o resultado aproximado destes métodos numéricos ía perdendo, entre outras cousas, a súa amplitude, podendo mesmo chegar a desaparecer completamente a onda. Ao contrario, había métodos que nin sequera miraban as ondas de alta frecuencia, é dicir, que non as comían. Pero ás veces iso tampouco era bo.
Cando estamos a liberar una ecuación diferencial de forma aproximada, é habitual dividir o campo no que debemos calcular a solución en elementos, é dicir, discretizar o problema. Os extremos de cada elemento denomínanse nodos. Una vez dividido o campo en elementos, aplícase ao problema o método numérico. Este problema terá uns autovalores, uns máis pequenos e outros máis grandes. Os pequenos autovalores proporciónannos ondas de baixa frecuencia e os grandes de alta frecuencia. E todos os autovalores do problema inflúen no resultado. O que pasa é que os grandes autobalios moitas veces son consecuencia da discretización, polo que non achegan nada ou nada bo no resultado final. Por tanto, cando estamos a liberar una ecuación diferencial mediante métodos numéricos, ademais dunha orde e una estabilidade, interésanos aplicar un método que consuma en parte esas ondas de alta frecuencia que poden ser consecuencia da discretización. É dicir, a clave do problema radica en que o método numérico que aplicaremos sexa capaz de moderar o consumo de ondas de alta frecuencia.
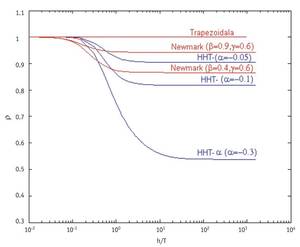
Cada método ten asociado un factor de amplificación. O maior módulo deste factor de amplificación denomínase radio espectral. O valor deste radio espectral depende, por outra banda, do tamaño e período do paso que imos dar no método co que liberaremos a ecuación diferencial. O radio espectral correspondente aos casos nos que ao dividir o tamaño do paso polo período obtense un valor baixo, mostra o comportamento do método numérico coas ondas de baixa frecuencia. Pola contra, o radio espectral correspondente aos casos nos que se obtén un número grande dividindo o tamaño do paso polo período, diranos como se comportará o método numérico con ondas de alta frecuencia. Si a medida que o tamaño do paso aumenta dividindo o período, diminúe o valor do radio espectral, isto significa que o método tenderá a amortecer as ondas de alta frecuencia.
Os métodos da familia de Newmark que se obteñen dando valores a dous parámetros (<,{) son de orde 2 paira{ = 1/2 e presentan unhas características de estabilidade bastante boas. Cando no método de Newmark tomamos os valores < = 1/4,{ = 1/2, obtense o chamado método trapezoidal, de orde 2 e cunha zona de estabilidade elevada. Ademais, o valor do radio espectral é sempre a unidade. Isto significa que manterá as ondas de alta e baixa frecuencia sen retardar nada. Isto é bo en parte, xa que co paso do tempo a onda manterase completa, pero doutra banda non é tan boa, xa que a amortiguación das ondas de alta frecuencia derivadas da discretización pode vir ben.
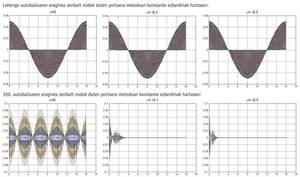
O método hht-? está construído en base ao método de Newmark e obtense mediante a asignación de valores a tres parámetros (?, <,{). E cando eliximos a e [-1/3, 0],{ = 1 - 2 a /2 e < = (1 - 2 a ) 2 /4, o método hht-? é de orde 2, ten boas características de estabilidade e ademais consegue amortecer a alta frecuencia. Isto é bo porque o método reducirá o efecto das altas frecuencias derivadas da discretización. Cando no método hht-? eliximos ? = 0 obtense a familia de Newmark. E tomando ? = 0 nas expresións de{ e < mencionadas, obtense o método trapezoidal da familia de Newmark.
A clave: adaptar a cada método o traballo que pode facer ben
Do mesmo xeito que noutros postos de traballo, a clave estaba na adecuación do traballo que mellor realizaría a cada método numérico. O responsable de persoal tiña una pregunta: uno dos requisitos que puñan no anuncio era que o método numérico que ían contratar era o gusto polas ondas de alta frecuencia, pero en que medida gustáballe?
O responsable de persoal dirixiuse ao método que acababa de entrevistar da seguinte maneira: "Téñoche que facer una pequena proba paira asegurar a túa orde e zona de estabilidade e calcular o teu radio espectral".
Una vez realizada a proba e una vez obtidos os resultados destas características por parte do responsable de persoal, procedeuse a corrixir o método da seguinte maneira: "vexo que tes capacidade paira actuar en ordes baixas. Tes una zona de estabilidade moi boa, case nada provócache estímulos. Ademais, no que respecta ao radio espectral, observo que só afecta en certa medida ás ondas de alta frecuencia, nin demasiado, nin demasiado. É adecuado paira os problemas que temos que soltar. Benvido á nosa empresa con experiencia en construción".
Así, a importante empresa bilbaína dedicada á construción de edificios contratou o método hht-alfa.