Una rondalla de mètodes numèrics: ... i per a menjar, ones d'alta freqüència
Mètodes numèrics
Les equacions diferencials van tenir una gran importància. Allí estaven quan calia estudiar una nova oportunitat de negoci en qualsevol empresa, fins i tot quan, aplicant uns tipus d'interès, es volia saber la quantitat de diners que hagués existit en els bancs al cap d'uns anys, o entre els enginyers d'una constructora, quan estaven estudiant les vibracions que podia suportar el nou pont que s'estava construint al poble veí, o en un laboratori de química quan s'anava a calcular la dispersió de temperatura d'una superfície... Totes elles van portar a diverses empreses i centres de recerca a identificar i definir la necessitat d'un nou lloc de treball, el corresponent al mètode numèric. El seu treball era resoldre analíticament, és a dir, alliberar equacions diferencials que no podien ser resoltes o que no interessaven resoldre exactament. Per a això, amb les operacions necessàries, obtenien una aproximació al resultat de l'equació diferencial.
Quan en algun lloc d'aquestes característiques calia contractar un mètode numèric, es posava un anunci en premsa, igual que en qualsevol altre lloc de treball. I així ho va fer també el responsable de personal que estava realitzant l'entrevista en aquest moment: "Una important empresa de l'entorn de Bilbao dedicada a la construcció d'edificis necessita un mètode numèric. Ha de ser capaç d'alliberar equacions diferencials en ordres baixos i poc influenciades per pertorbacions o problemes derivats del mitjà. Es valorarà experiència en la resolució de problemes relacionats amb vibracions. El gust per les ones d'alta freqüència és fonamental. Ofereix un bon sou i la possibilitat d'utilitzar el gimnàs de l'empresa."
S'analitzaven els currículums dels candidats rebuts per al lloc. El mètode numèric tenia en compte les capacitats intel·lectuals i psicològiques. Entre els intel·lectuals es tenia en compte la precisió amb la qual el mètode podia resoldre l'equació diferencial. "He estat dissenyat i programat per a resoldre problemes amb precisió en diferents ordres", afirmava un que per al resultat aproximat buscat l'empresa podia resoldre les equacions diferencials amb la precisió (gran o petita) desitjada. Uns altres només treballaven en primer o segon ordre, és a dir, en ordres baixos i per tant amb poca precisió. Quan el projecte que tenia en mans l'empresa necessitava major precisió, no es contractaven els que alliberaven en baixos ordres. Això no significava que no existissin empreses per a la contractació de treballadors que treballaven per aquestes ordres, que en unes altres podien haver estat contractats, per descomptat.
Quant a les capacitats psicològiques, l'empresa contractant desitjava conèixer el camp d'estabilitat del mètode numèric. Això determinava la resposta del mètode davant errors o pertorbacions que es produïen en alliberar les equacions. El mètode també reflectia la seva capacitat de familiaritzar-se amb les peculiaritats de l'equació diferencial --autovalores -. El fet que el mètode tingués un camp d'estabilitat ampli indicava que tenia capacitat d'actuar davant problemes diversos. Una àrea d'estabilitat més petita, no obstant això, podia demostrar que davant certes pertorbacions el mètode no donaria resultats satisfactoris. En aquests casos, les pertorbacions en els problemes resolts fora de la zona d'estabilitat augmentaven i el resultat calculat podia arribar a ser menys bo o dolent.
Quant cobres? "Per cost computacional". El que era capaç de treballar en ordres alts i d'evitar pertorbacions era costós. Així, el treball de diversos matemàtics se centrava en el disseny d'aquests mètodes.
Ràdio espectral
No obstant això, hi havia alguna característica que s'ocultava més pel mètode numèric. Una de les característiques ocultes era el denominat amortiment algorítmic. El que mostrava el comportament del mètode amb ones d'alta freqüència.

Existien mètodes numèrics d'ordre alt i estable però que no tenien bon comportament amb ones d'alta freqüència. Això significava que quan estàvem alliberant les equacions diferencials en les quals apareixien altes freqüències hi havia mètodes que tendien a abusar de les altes freqüències. En les equacions diferencials en forma d'ona, si teòricament l'ona estava vibrant en un interval de temps, el resultat aproximat d'aquests mètodes numèrics anava perdent, entre altres coses, la seva amplitud, podent fins i tot arribar a desaparèixer completament l'ona. Al contrari, hi havia mètodes que ni tan sols miraven les ones d'alta freqüència, és a dir, que no les menjaven. Però a vegades això tampoc era bo.
Quan estem alliberant una equació diferencial de manera aproximada, és habitual dividir el camp en el qual hem de calcular la solució en elements, és a dir, discretizar el problema. Els extrems de cada element es denominen nodes. Una vegada dividit el camp en elements, s'aplica al problema el mètode numèric. Aquest problema tindrà uns autovalores, uns més petits i uns altres més grans. Els petits autovalores ens proporcionen ones de baixa freqüència i els grans d'alta freqüència. I tots els autovalores del problema influeixen en el resultat. El que passa és que els grans autobalios moltes vegades són conseqüència de la discretización, per la qual cosa no aporten res o gens bo en el resultat final. Per tant, quan estem alliberant una equació diferencial mitjançant mètodes numèrics, a més d'un ordre i una estabilitat, ens interessa aplicar un mètode que consumeixi en part aquestes ones d'alta freqüència que poden ser conseqüència de la discretización. És a dir, la clau del problema radica en el fet que el mètode numèric que aplicarem sigui capaç de moderar el consum d'ones d'alta freqüència.
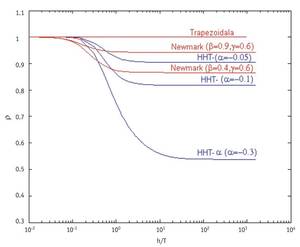
Cada mètode té associat un factor d'amplificació. El major mòdul d'aquest factor d'amplificació es denomina ràdio espectral. El valor d'aquest radi espectral depèn, d'altra banda, de la grandària i període del pas que donarem en el mètode amb el qual alliberarem l'equació diferencial. El radi espectral corresponent als casos en els quals en dividir la grandària del pas pel període s'obté un valor baix, mostra el comportament del mètode numèric amb les ones de baixa freqüència. Per contra, el radi espectral corresponent als casos en els quals s'obté un número gran dividint la grandària del pas pel període, ens dirà com es comportarà el mètode numèric amb ones d'alta freqüència. Si a mesura que la grandària del pas augmenta dividint el període, disminueix el valor del radi espectral, això significa que el mètode tendirà a esmorteir les ones d'alta freqüència.
Els mètodes de la família de Newmark que s'obtenen donant valors a dos paràmetres (<,{) són d'ordre 2 per a{ = 1/2 i presenten unes característiques d'estabilitat bastant bones. Quan en el mètode de Newmark prenem els valors < = 1/4,{ = 1/2, s'obté l'anomenat mètode trapezoidal, d'ordre 2 i amb una zona d'estabilitat elevada. A més, el valor del radi espectral és sempre la unitat. Això significa que mantindrà les ones d'alta i baixa freqüència sense alentir res. Això és bo en part, ja que amb el pas del temps l'ona es mantindrà completa, però d'altra banda no és tan bona, ja que l'amortiment de les ones d'alta freqüència derivades de la discretización pot venir bé.
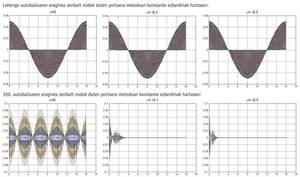
El mètode hht-? està construït sobre la base del mètode de Newmark i s'obté mitjançant l'assignació de valors a tres paràmetres (?, <,{). I quan triem a e [-1/3, 0],{ = 1 - 2 a /2 i < = (1 - 2 a ) 2 /4, el mètode hht-? és d'ordre 2, té bones característiques d'estabilitat i a més aconsegueix esmorteir l'alta freqüència. Això és bo perquè el mètode reduirà l'efecte de les altes freqüències derivades de la discretización. Quan en el mètode hht-? triem ? = 0 s'obté la família de Newmark. I prenent ? = 0 en les expressions de{ i < esmentades, s'obté el mètode trapezoidal de la família de Newmark.
La clau: adaptar a cada mètode el treball que pot fer bé
Igual que en altres llocs de treball, la clau estava en l'adequació del treball que millor realitzaria a cada mètode numèric. El responsable de personal tenia una pregunta: un dels requisits que posaven en l'anunci era que el mètode numèric que anaven a contractar era el gust per les ones d'alta freqüència, però en quina mesura li agradava?
El responsable de personal es va dirigir al mètode que acabava d'entrevistar de la següent manera: "T'haig de fer una petita prova per a assegurar la teva ordre i zona d'estabilitat i calcular el teu radi espectral".
Una vegada realitzada la prova i una vegada obtinguts els resultats d'aquestes característiques per part del responsable de personal, es va procedir a corregir el mètode de la següent manera: "veig que tens capacitat per a actuar en ordres baixos. Tens una zona d'estabilitat molt bona, gairebé res et provoca estímuls. A més, pel que fa al radi espectral, observo que només afecta en certa manera a les ones d'alta freqüència, ni massa, ni massa. És adequat per als problemes que hem de deixar anar. Benvingut a la nostra empresa amb experiència en construcció".
Així, la important empresa bilbaïna dedicada a la construcció d'edificis va contractar el mètode hht-alfa.