Una fábula de métodos numéricos: ... y para comer, ondas de alta frecuencia
Métodos numéricos
Las ecuaciones diferenciales tuvieron una gran importancia. Allí estaban cuando había que estudiar una nueva oportunidad de negocio en cualquier empresa, incluso cuando, aplicando unos tipos de interés, se quería saber la cantidad de dinero que hubiera existido en los bancos al cabo de unos años, o entre los ingenieros de una constructora, cuando estaban estudiando las vibraciones que podía soportar el nuevo puente que se estaba construyendo en el pueblo vecino, o en un laboratorio de química cuando se iba a calcular la dispersión de temperatura de una superficie... Todas ellas llevaron a diversas empresas y centros de investigación a identificar y definir la necesidad de un nuevo puesto de trabajo, el correspondiente al método numérico. Su trabajo era resolver analíticamente, es decir, liberar ecuaciones diferenciales que no podían ser resueltas o que no interesaban resolver exactamente. Para ello, con las operaciones necesarias, obtenían una aproximación al resultado de la ecuación diferencial.
Cuando en algún lugar de estas características había que contratar un método numérico, se ponía un anuncio en prensa, al igual que en cualquier otro puesto de trabajo. Y así lo hizo también el responsable de personal que estaba realizando la entrevista en ese momento: "Una importante empresa del entorno de Bilbao dedicada a la construcción de edificios necesita un método numérico. Debe ser capaz de liberar ecuaciones diferenciales en órdenes bajos y poco influenciadas por perturbaciones o problemas derivados del medio. Se valorará experiencia en la resolución de problemas relacionados con vibraciones. El gusto por las ondas de alta frecuencia es fundamental. Ofrece un buen sueldo y la posibilidad de utilizar el gimnasio de la empresa."
Se analizaban los currículos de los candidatos recibidos para el puesto. El método numérico tenía en cuenta las capacidades intelectuales y psicológicas. Entre los intelectuales se tenía en cuenta la precisión con la que el método podía resolver la ecuación diferencial. "He sido diseñado y programado para resolver problemas con precisión en distintos órdenes", afirmaba uno que para el resultado aproximado buscado la empresa podía resolver las ecuaciones diferenciales con la precisión (grande o pequeña) deseada. Otros sólo trabajaban en primer o segundo orden, es decir, en órdenes bajos y por tanto con poca precisión. Cuando el proyecto que tenía en manos la empresa necesitaba mayor precisión, no se contrataban los que liberaban en bajos órdenes. Esto no significaba que no existieran empresas para la contratación de trabajadores que trabajaban por estas órdenes, que en otras podían haber sido contratados, por supuesto.
En cuanto a las capacidades psicológicas, la empresa contratante deseaba conocer el campo de estabilidad del método numérico. Esto determinaba la respuesta del método ante errores o perturbaciones que se producían al liberar las ecuaciones. El método también reflejaba su capacidad de familiarizarse con las peculiaridades de la ecuación diferencial --autovalores -. El hecho de que el método tuviera un campo de estabilidad amplio indicaba que tenía capacidad de actuar ante problemas diversos. Un área de estabilidad más pequeña, sin embargo, podía demostrar que ante ciertas perturbaciones el método no daría resultados satisfactorios. En estos casos, las perturbaciones en los problemas resueltos fuera de la zona de estabilidad aumentaban y el resultado calculado podía llegar a ser menos bueno o malo.
¿Cuánto cobras? "Por coste computacional". Lo que era capaz de trabajar en órdenes altos y de evitar perturbaciones era costoso. Así, el trabajo de varios matemáticos se centraba en el diseño de estos métodos.
Radio espectral
Sin embargo, había alguna característica que se ocultaba más por el método numérico. Una de las características ocultas era la denominada amortiguación algorítmica. Lo que mostraba el comportamiento del método con ondas de alta frecuencia.

Existían métodos numéricos de orden alto y estable pero que no tenían buen comportamiento con ondas de alta frecuencia. Esto significaba que cuando estábamos liberando las ecuaciones diferenciales en las que aparecían altas frecuencias había métodos que tendían a abusar de las altas frecuencias. En las ecuaciones diferenciales en forma de onda, si teóricamente la onda estaba vibrando en un intervalo de tiempo, el resultado aproximado de estos métodos numéricos iba perdiendo, entre otras cosas, su amplitud, pudiendo incluso llegar a desaparecer completamente la onda. Al contrario, había métodos que ni siquiera miraban las ondas de alta frecuencia, es decir, que no las comían. Pero a veces eso tampoco era bueno.
Cuando estamos liberando una ecuación diferencial de forma aproximada, es habitual dividir el campo en el que debemos calcular la solución en elementos, es decir, discretizar el problema. Los extremos de cada elemento se denominan nodos. Una vez dividido el campo en elementos, se aplica al problema el método numérico. Este problema tendrá unos autovalores, unos más pequeños y otros más grandes. Los pequeños autovalores nos proporcionan ondas de baja frecuencia y los grandes de alta frecuencia. Y todos los autovalores del problema influyen en el resultado. Lo que pasa es que los grandes autobalios muchas veces son consecuencia de la discretización, por lo que no aportan nada o nada bueno en el resultado final. Por lo tanto, cuando estamos liberando una ecuación diferencial mediante métodos numéricos, además de un orden y una estabilidad, nos interesa aplicar un método que consuma en parte esas ondas de alta frecuencia que pueden ser consecuencia de la discretización. Es decir, la clave del problema radica en que el método numérico que aplicaremos sea capaz de moderar el consumo de ondas de alta frecuencia.
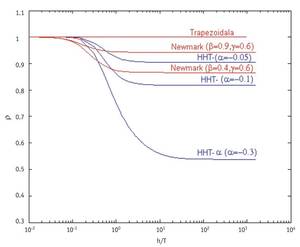
Cada método tiene asociado un factor de amplificación. El mayor módulo de este factor de amplificación se denomina radio espectral. El valor de este radio espectral depende, por otra parte, del tamaño y periodo del paso que vamos a dar en el método con el que liberaremos la ecuación diferencial. El radio espectral correspondiente a los casos en los que al dividir el tamaño del paso por el período se obtiene un valor bajo, muestra el comportamiento del método numérico con las ondas de baja frecuencia. Por el contrario, el radio espectral correspondiente a los casos en los que se obtiene un número grande dividiendo el tamaño del paso por el período, nos dirá cómo se comportará el método numérico con ondas de alta frecuencia. Si a medida que el tamaño del paso aumenta dividiendo el periodo, disminuye el valor del radio espectral, esto significa que el método tenderá a amortiguar las ondas de alta frecuencia.
Los métodos de la familia de Newmark que se obtienen dando valores a dos parámetros (<,{) son de orden 2 para{ = 1/2 y presentan unas características de estabilidad bastante buenas. Cuando en el método de Newmark tomamos los valores < = 1/4,{ = 1/2, se obtiene el llamado método trapezoidal, de orden 2 y con una zona de estabilidad elevada. Además, el valor del radio espectral es siempre la unidad. Esto significa que mantendrá las ondas de alta y baja frecuencia sin ralentizar nada. Esto es bueno en parte, ya que con el paso del tiempo la onda se mantendrá completa, pero por otro lado no es tan buena, ya que la amortiguación de las ondas de alta frecuencia derivadas de la discretización puede venir bien.
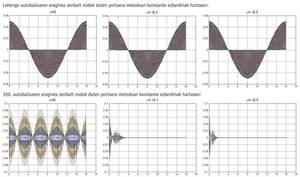
El método hht-? está construido en base al método de Newmark y se obtiene mediante la asignación de valores a tres parámetros (?, <,{). Y cuando elegimos a e [-1/3, 0],{ = 1 - 2 a /2 y < = (1 - 2 a ) 2 /4, el método hht-? es de orden 2, tiene buenas características de estabilidad y además consigue amortiguar la alta frecuencia. Esto es bueno porque el método reducirá el efecto de las altas frecuencias derivadas de la discretización. Cuando en el método hht-? elegimos ? = 0 se obtiene la familia de Newmark. Y tomando ? = 0 en las expresiones de{ y < mencionadas, se obtiene el método trapezoidal de la familia de Newmark.
La clave: adaptar a cada método el trabajo que puede hacer bien
Al igual que en otros puestos de trabajo, la clave estaba en la adecuación del trabajo que mejor realizaría a cada método numérico. El responsable de personal tenía una pregunta: uno de los requisitos que ponían en el anuncio era que el método numérico que iban a contratar era el gusto por las ondas de alta frecuencia, pero ¿en qué medida le gustaba?
El responsable de personal se dirigió al método que acababa de entrevistar de la siguiente manera: "Te tengo que hacer una pequeña prueba para asegurar tu orden y zona de estabilidad y calcular tu radio espectral".
Una vez realizada la prueba y una vez obtenidos los resultados de estas características por parte del responsable de personal, se procedió a corregir el método de la siguiente manera: "veo que tienes capacidad para actuar en órdenes bajos. Tienes una zona de estabilidad muy buena, casi nada te provoca estímulos. Además, en lo que respecta al radio espectral, observo que sólo afecta en cierta medida a las ondas de alta frecuencia, ni demasiado, ni demasiado. Es adecuado para los problemas que tenemos que soltar. Bienvenido a nuestra empresa con experiencia en construcción".
Así, la importante empresa bilbaína dedicada a la construcción de edificios contrató el método hht-alfa.