Une fable de méthodes numériques: ... et à manger, ondes à haute fréquence
Méthodes numériques
Les équations différentielles ont eu une grande importance. Ils étaient là quand il fallait étudier une nouvelle opportunité d'affaires dans n'importe quelle entreprise, même quand, en appliquant des taux d'intérêt, on voulait savoir combien d'argent aurait existé dans les banques au bout de quelques années, ou parmi les ingénieurs d'un constructeur, quand ils étudiaient les vibrations qui pouvaient supporter le nouveau pont qui était en construction dans le village voisin, ou dans un laboratoire de chimie quand on allait calculer la dispersion de température d'une surface..... Elles ont toutes amené diverses entreprises et centres de recherche à identifier et définir la nécessité d'un nouveau poste de travail, celui correspondant à la méthode numérique. Son travail consistait à résoudre analytiquement, c'est-à-dire à libérer des équations différentielles qui ne pouvaient être résolues ou qui n'intéressaient pas à résoudre exactement. Pour cela, avec les opérations nécessaires, ils ont obtenu une approche du résultat de l'équation différentielle.
Lorsque, quelque part dans ces caractéristiques, il fallait embaucher une méthode numérique, on mettait une annonce dans la presse, comme dans tout autre poste de travail. Et c'est ce que fit aussi le responsable du personnel qui réalisait l'interview à ce moment-là: "Une importante entreprise de l'environnement de Bilbao dédiée à la construction de bâtiments a besoin d'une méthode numérique. Il doit être en mesure de libérer des équations différentielles dans des ordres faibles et peu influencés par des perturbations ou des problèmes dérivés du milieu. Une expérience de résolution des problèmes liés aux vibrations sera évaluée. Le goût pour les ondes à haute fréquence est fondamental. Il offre un bon salaire et la possibilité d'utiliser la salle de gym de l'entreprise."
Les programmes des candidats reçus pour le poste étaient analysés. La méthode numérique tenait compte des capacités intellectuelles et psychologiques. Parmi les intellectuels, il était tenu compte de la précision avec laquelle la méthode pouvait résoudre l'équation différentielle. "J'ai été conçu et programmé pour résoudre des problèmes avec précision dans différents ordres", a affirmé un que pour le résultat approximatif recherché l'entreprise pouvait résoudre les équations différentielles avec la précision (grande ou petite) souhaitée. D'autres travaillaient seulement dans le premier ou le second ordre, c'est-à-dire dans des ordres bas et donc avec peu de précision. Lorsque le projet qui était entre les mains de l'entreprise avait besoin d'une plus grande précision, ceux qui libéraient sous de faibles ordres n'étaient pas embauchés. Cela ne signifiait pas qu'il n'y avait pas d'entreprises pour embaucher des travailleurs qui travaillaient pour ces ordres, qui dans d'autres pourraient avoir été embauchés, bien sûr.
Quant aux capacités psychologiques, l'entreprise contractante souhaitait connaître le champ de stabilité de la méthode numérique. Cela déterminait la réponse de la méthode aux erreurs ou perturbations qui se produisaient en libérant les équations. La méthode reflétait également sa capacité à se familiariser avec les particularités de l'équation différentielle --valeurs de soi -. Le fait que la méthode ait un champ de stabilité large indiquait qu'elle avait la capacité d'agir face à des problèmes divers. Une zone de stabilité plus petite, cependant, pouvait démontrer que face à certaines perturbations la méthode ne donnerait pas de résultats satisfaisants. Dans ces cas, les perturbations des problèmes résolus en dehors de la zone de stabilité augmentaient et le résultat calculé pouvait devenir moins bon ou mauvais.
Combien de cobras? "Pour coût informatique". Ce qui était capable de travailler sur des ordres élevés et d'éviter des perturbations était coûteux. Ainsi, le travail de plusieurs mathématiciens se concentrait sur la conception de ces méthodes.
Radio spectrale
Cependant, il y avait une caractéristique qui était plus cachée par la méthode numérique. Une des caractéristiques cachées était le soi-disant amortissement algorithmique. Ce qui montrait le comportement de la méthode avec des ondes à haute fréquence.

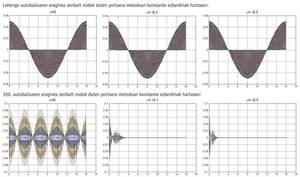
Il existait des méthodes numériques d'ordre élevé et stable, mais qui n'avaient pas de bon comportement avec des ondes à haute fréquence. Cela signifiait que lorsque nous étions en libérant les équations différentielles dans lesquelles apparaissaient hautes fréquences, il y avait des méthodes qui tendaient à abuser des hautes fréquences. Dans les équations différentielles en forme d'onde, si théoriquement l'onde vibrait dans un intervalle de temps, le résultat approximatif de ces méthodes numériques perdait, entre autres, leur amplitude, pouvant même arriver à disparaître complètement l'onde. Au contraire, il y avait des méthodes qui ne regardaient même pas les ondes à haute fréquence, c'est-à-dire qui ne les mangeaient pas. Mais parfois, ce n'était pas bon.
Lorsque nous libérons une équation différentielle d'une manière approximative, il est courant de diviser le champ dans lequel nous devons calculer la solution en éléments, c'est-à-dire discrétiser le problème. Les extrémités de chaque élément sont appelées nœuds. Une fois le champ divisé en éléments, la méthode numérique est appliquée au problème. Ce problème aura des autovaleurs, des plus petites et des plus grandes. Les petites valeurs automatiques nous fournissent des ondes à basse fréquence et les grandes à haute fréquence. Et toutes les valeurs personnelles du problème influencent le résultat. Ce qui se passe, c'est que les grands autobus sont souvent la conséquence de la discrétisation, donc ils n'apportent rien ou rien de bon dans le résultat final. Par conséquent, lorsque nous libérons une équation différentielle par des méthodes numériques, en plus d'un ordre et une stabilité, nous sommes intéressés à appliquer une méthode qui consomme en partie ces ondes à haute fréquence qui peuvent être la conséquence de la discrétisation. C'est-à-dire que la clé du problème est que la méthode numérique que nous appliquerons soit capable de modérer la consommation d'ondes à haute fréquence.
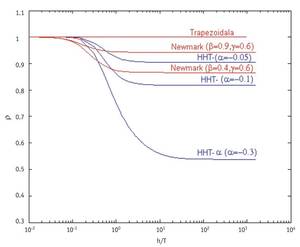
Chaque méthode a associé un facteur d'amplification. Le plus grand module de ce facteur d'amplification est appelé rayon spectral. La valeur de ce rayon spectral dépend, d'autre part, de la taille et de la période du passage que nous allons donner dans la méthode avec laquelle nous libérerons l'équation différentielle. Le rayon spectral correspondant aux cas où en divisant la taille du passage par la période on obtient une faible valeur, montre le comportement de la méthode numérique avec les ondes à basse fréquence. Au contraire, le rayon spectral correspondant aux cas où on obtient un grand nombre en divisant la taille du passage par la période, nous dira comment la méthode numérique se comportera avec des ondes à haute fréquence. Si la taille du pas augmente en divisant la période, la valeur du rayon spectral diminue, cela signifie que la méthode aura tendance à amortir les ondes à haute fréquence.
Les méthodes de la famille de Newmark qui sont obtenues en donnant des valeurs à deux paramètres (,{) sont d'ordre 2 pour{ = 1/2 et présentent des caractéristiques de stabilité assez bonnes. Lorsque nous prenons dans la méthode de Newmark les valeurs mobilières = 1/4,{ = 1/2, on obtient la méthode dite trapézoïdale, d'ordre 2 et avec une zone de stabilité élevée. En outre, la valeur du rayon spectral est toujours l'unité. Cela signifie qu'il maintiendra les ondes à haute et basse fréquence sans ralentir quoi que ce soit. C'est bon en partie, car avec le passage du temps l'onde restera complète, mais d'autre part ce n'est pas si bon, puisque l'absorption des ondes à haute fréquence dérivées de la discrétisation peut venir bien.
La méthode hht-? est construite sur la base de la méthode Newmark et est obtenue en assignant des valeurs à trois paramètres (?,{). Et quand on choisit e [-1/3, 0],{ = 1 - 2 a /2 et = (1 - 2 a ) 2 /4, la méthode hht-? est d'ordre 2, elle a de bonnes caractéristiques de stabilité et elle réussit aussi à amortir la haute fréquence. C'est bon parce que la méthode réduira l'effet des hautes fréquences dérivées de la discrétisation. Quand dans la méthode hht-? nous choisissons = 0 nous obtenons la famille de Newmark. Et en prenant ? = 0 dans les expressions d'âme mentionnées ci-dessus, on obtient la méthode trapézoïdale de la famille de Newmark.
La clé: adapter à chaque méthode le travail qui peut bien faire
Comme dans d'autres emplois, la clé était d'adapter le travail que je ferais le mieux à chaque méthode numérique. Le responsable du personnel avait une question: l'une des exigences qu'ils mettaient dans l'annonce était que la méthode numérique qu'ils allaient embaucher était le goût des ondes à haute fréquence, mais dans quelle mesure aimez-vous?
Le responsable du personnel s'est adressé à la méthode qu'il venait d'interviewer comme suit: "Je dois faire un petit test pour assurer votre ordre et votre zone de stabilité et calculer votre rayon spectral".
Une fois le test effectué et une fois les résultats de ces caractéristiques obtenus par le responsable du personnel, la méthode a été corrigée comme suit: "Je vois que vous avez la capacité d'agir dans des ordres bas. Vous avez une très bonne zone de stabilité, presque rien ne vous provoque des stimuli. De plus, en ce qui concerne le rayon spectral, je constate qu'il n'affecte dans une certaine mesure que les ondes à haute fréquence, ni trop, ni trop. Il est adapté pour les problèmes que nous devons lâcher. Bienvenue dans notre entreprise avec une expérience de construction".
Ainsi, l'importante entreprise bilbaïne dédiée à la construction de bâtiments a embauché la méthode hht-alpha.