Cadea de ouro e...
O xogo que creou moitos rumores nos últimos tempos é a cadea de ouro. Xa se dixo moito sobre este xogo en medios de comunicación, televisión, xornais, radio. Nós aquí relacionaremos este xogo coas matemáticas.
Empecemos polo desenvolvemento do xogo e vexamos como se poden gañar 40.960.000 pesetas. Supomos que a persoa A compra una lista. Una vez adquirida a lista, deberá abonar á primeira persoa que apareza nela 5.000 pesetas. Como pagou outras 5.000 pesetas pola lista, de momento perdeu 10.000 pesetas. Agora ten que quitar o primeiro nome da lista e o seu no lugar 12, é dicir, escribir.
Esta nova lista deberá ser vendida a dúas persoas. Se estes dous son B e C, estes terán na súa lista o nome da en 12º lugar (neste momento A recupera 10.000 pesetas, polo que non perdeu nada). As persoas B e C deben pasar as listas a outras dúas persoas, como D, E, F e G. Nas listas destas catro persoas atopariamos o nome da no posto 11. No seguinte paso 8 serán as persoas que teñan o nome da en 10º lugar na lista. A próxima vez 16 persoas terán o nome da na 9ª praza. Non é difícil estimar que o número de persoas que teñen o nome da en 1ª posición é 4.096.
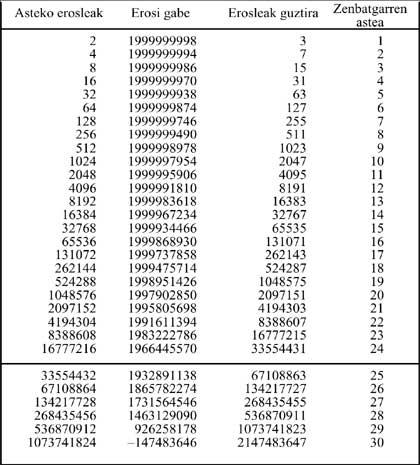
Estes últimos deben vender as listas a 8.192 persoas, en todas estas listas o nome da está en 1ª posición. Por tanto, estas 8.192 persoas terán que pagar á cinco mil pesetas paira comprar a lista, é dicir, A debería cobrar 8.192 x 5.000 = 40.960.00 pesetas (se todo salgue ben). Á espera de seguir mellor o exposto, achégase a táboa con todos os pasos do proceso:

Até aquí fixemos una descrición do xogo. Nesta descrición obsérvase un importante incremento do número de persoas. Ao final do artigo falaremos disto e de grandes números. Aquí mencionamos as palabras xogo e diñeiro, e agora resúltanos difícil non mencionar outros xogos de azar que coñecemos paira gañar diñeiro rápido.
Nesta ocasión imos proceder ao cálculo aproximado das probabilidades destes xogos.
Non podemos considerar a cadea de ouro como un xogo de azar. Cal é a probabilidade de vender una lista? Eu coñezo a un amigo que vendeu as dúas listas un día, pero tamén a un amigo que pasou dúas semanas e non vendeu ningunha lista. Non falamos, por tanto, da probabilidade deste xogo, pero si dos demais.
Quinielas
Paira empezar, por que non, analizaremos as quinielas. Por suposto, neste xogo o factor humano ten a súa importancia, non o negaremos (1, X, 2 non teñen a mesma probabilidade de saír nos partidos Real-Sabadell ou Osasuna-Atletia de Bilbao).
Pero desde o punto de vista da persoa que fai a aposta, a cada partido poderiámoslle pór 1, X ou 2, acertando só cun, é dicir, a probabilidade de acertar será de 1/3. Probabilidade de adiviñar dous partidos 1/3 . 1/3 (primeira e segunda). Por tanto, sería a probabilidade de acertar os 14 partidos (todo iso cunha columna por suposto).

Con dous ou tres símbolos aumentará a probabilidade. A maior aposta múltiple é de 5 triplos e 2 dobres. Isto supón 972 apostas. Por tanto, neste caso a probabilidade é de 0,0002032 (é dicir, de 4.921 apostas só una posibilidade). Como se pode observar, aínda que se avanzou moito, non se alcanzou a décima parte, e a cantidade a gastar é de 19.440 pesetas (non analizaremos aquí os desenvolvementos abreviados).
Seguiremos coa lotaría. O factor humano non inflúe neste xogo. Hai moitos premios na lotaría, pero o maior só corresponde a un dos 80.000 números. Probabilidade neste caso
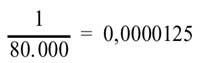
é, baixo en absoluto. Hai un premio chamado pedrea (como todos sabemos, se a última cifra do teu número coincide co premio principal, devólvenche o que xogas). Tendo en conta que nun sorteo ordinario hai aproximadamente 1.200 premios (sen contar os finais), a probabilidade de conseguir un premio é de 0,015 (é dicir, só una de cada 67 probabilidades), non está mal comparada coa quiniela.
Loto
O sistema de sorteo do loto é totalmente diferente. O xogador deberá elixir 6 do 49. As probabilidades de ser premiado preséntanse na seguinte táboa.

Aquí non analizaremos os casos nos que se realizan múltiples apostas nun cadrado. (No caso máis sinxelo, como se pode observar, só una das 1055 é paira gañar).
No novo xogo BONO-LOTO as probabilidades son 4 veces maiores, xa que una mesma aposta participa en 4 sorteos. Serán as seguintes:

(No caso máis sinxelo, de 263 apostas, só hai una posibilidade).
Sorteo de cegos
No sorteo da ONCE só hai 5 premios. Participan 100.000 números. A probabilidade de obter o Premio Principal é de 1/10 5, é dicir, 0,00001. A probabilidade de obter o segundo premio (pero non o primeiro) é de 9/10 5 = 0,00009. A terceira (e non as dous anteriores) obtense cunha probabilidade de 9/10 4 = 0,9. Paira obter o cuarto (e non os anteriores) a probabilidade é de 9/10 3 = 0,009 e por último a probabilidade de alcanzar só o quinto é de 9/10 2 = 0,09. (Se se consegue un premio, hai que ter en conta que non se poden conseguir premios inferiores) Pero a probabilidade de obter polo menos un premio é de 1/10 = 0,1 (isto corresponde a acertar a última cifra).
Até agora dixemos o relativo ás probabilidades de xogos de azar coñecidos. Como se ve, non é fácil conseguir diñeiro con estes métodos.
Cadea de ouro
Agora, e como prometía, imos falar do aumento do número de persoas que participan no xogo da Cadea de Ouro e dos grandes números.
Supoñamos que una persoa necesita una semana paira vender dúas listas. No Estado prevese que a compra da lista sexa de 20.000.000 de habitantes. Como se pode observar na seguinte listaxe, na semana 23, 8.388.608 comprarían una lista, quedando 3.222.786 persoas sen lista, ver táboa orixinal. A semana seguinte habería que vender 16.777.216 listas. Se nos aseguramos de que cada persoa compra una soa lista, non quedarían amigos paira comprar todas as listas. É dicir,
Utilizouse una lista paira indicar. Pero é sorprendente saber que tomando a metade da poboación mundial, é dicir, 2.000 millóns de persoas, o xogo terminaría na semana 29 (é dicir, só 6 semanas despois), como se pode ver na seguinte lista.
Paira terminar
Colle agora un papel e non digas máis ou menos cantas veces podes dobrar. Próbao cun folio. Conseguíchelo? Que non? Colle una páxina máis grande, por exemplo a dobre páxina do xornal e volve tentalo. Cantas veces dobrou? Supoñamos que o espesor dunha folla é de 0,001 cm. Se encartamos a folla una vez obtemos o espesor de dúas follas. Volvendo dobrar, o grosor das catro follas e de seguir así, encartándoas en 50 veces obteriamos o espesor de 2 50 = 1.125.699.906.842.624 follas, é dicir:

é dicir, máis de once millóns de quilómetros de espesor. Na práctica demostrouse que se pode encartar até 8 veces. Se falamos de números grandes, imos facer dúas preguntas paira terminar o artigo: canto tardaría en contar un millón de números partindo de 1 (un, dous, ...)? e contar un billón? (Calcula os números que contas nun minuto).