Cadena d'or i...
El joc que ha creat molts rumors en els últims temps és la cadena d'or. Ja s'ha dit molt de sobre aquest joc en mitjans de comunicació, televisió, periòdics, ràdio. Nosaltres aquí relacionarem aquest joc amb les matemàtiques.
Comencem pel desenvolupament del joc i vegem com es poden guanyar 40.960.000 pessetes. Suposem que la persona A compra una llista. Una vegada adquirida la llista, haurà d'abonar a la primera persona que aparegui en ella 5.000 pessetes. Com va pagar altres 5.000 pessetes per la llista, de moment ha perdut 10.000 pessetes. Ara ha de llevar el primer nom de la llista i el seu en el lloc 12, és a dir, escriure.
Aquesta nova llista haurà de ser venuda a dues persones. Si aquests dos són B i C, aquests tindran en la seva llista el nom d'en 12è lloc (en aquest moment A recupera 10.000 pessetes, per la qual cosa no ha perdut res). Les persones B i C han de passar les llistes a altres dues persones, com a D, E, F i G. En les llistes d'aquestes quatre persones trobaríem el nom d'en el lloc 11. En el següent pas 8 seran les persones que tinguin el nom d'en 10è lloc en la llista. La pròxima vegada 16 persones tindran el nom d'en la 9a plaça. No és difícil estimar que el nombre de persones que tenen el nom d'en 1a posició és 4.096.
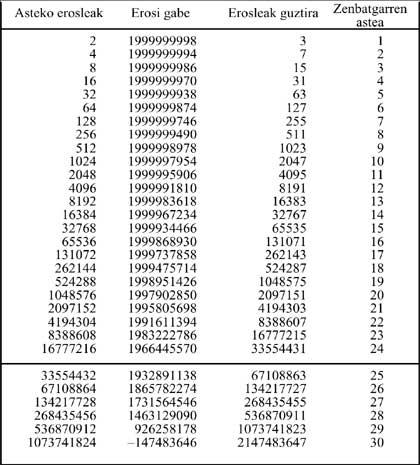
Aquests últims han de vendre les llistes a 8.192 persones, en totes aquestes llistes el nom d'està en 1a posició. Per tant, aquestes 8.192 persones hauran de pagar a A cinc mil pessetes per a comprar la llista, és a dir, A hauria de cobrar 8.192 x 5.000 = 40.960.00 pessetes (si tot surt bé). A l'espera de seguir millor l'exposat, s'adjunta la taula amb tots els passos del procés:

Fins aquí hem fet una descripció del joc. En aquesta descripció s'observa un important increment del nombre de persones. Al final de l'article parlarem d'això i de grans números. Aquí hem esmentat les paraules jugo i diners, i ara ens resulta difícil no esmentar altres jocs d'atzar que coneixem per a guanyar diners ràpids.
En aquesta ocasió procedirem al càlcul aproximat de les probabilitats d'aquests jocs.
No podem considerar la cadena d'or com un joc d'atzar. Quina és la probabilitat de vendre una llista? Jo conec a un amic que ha venut les dues llistes un dia, però també a un amic que ha passat dues setmanes i no ha venut cap llista. No parlem, per tant, de la probabilitat d'aquest joc, però sí dels altres.
Travesses
Per a començar, per què no, analitzarem les travesses. Per descomptat, en aquest joc el factor humà té la seva importància, no el negarem (1, X, 2 no tenen la mateixa probabilitat de sortir en els partits Real-Sabadell o Osasuna-Atletia de Bilbao).
Però des del punt de vista de la persona que fa l'aposta, a cada partit li podríem posar 1, X o 2, encertant només amb un, és a dir, la probabilitat d'encertar serà de 1/3. Probabilitat d'endevinar dos partits 1/3 . 1/3 (primera i segona). Per tant, seria la probabilitat d'encertar els 14 partits (tot això amb una columna per descomptat).

Amb dos o tres símbols augmentarà la probabilitat. La major aposta múltiple és de 5 triples i 2 dobles. Això suposa 972 apostes. Per tant, en aquest cas la probabilitat és de 0,0002032 (és a dir, de 4.921 apostes només una possibilitat). Com es pot observar, encara que s'ha avançat molt, no s'ha aconseguit la desena part, i la quantitat a gastar és de 19.440 pessetes (no analitzarem aquí els desenvolupaments abreujats).
Seguirem amb la loteria. El factor humà no influeix en aquest joc. Hi ha molts premis en la loteria, però el major només correspon a un dels 80.000 números. Probabilitat en aquest cas
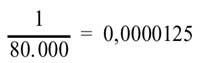
és, baix en absolut. Hi ha un premi anomenat pedrea (com tots sabem, si l'última xifra del teu número coincideix amb el premi principal, et retornen el que jugues). Tenint en compte que en un sorteig ordinari hi ha aproximadament 1.200 premis (sense comptar els finals), la probabilitat d'aconseguir un premi és de 0,015 (és a dir, només una de cada 67 probabilitats), no està mal comparada amb el travessa.
Lotus
El sistema de sorteig del lotus és totalment diferent. El jugador haurà de triar 6 del 49. Les probabilitats de ser premiat es presenten en la següent taula.

Aquí no analitzarem els casos en els quals es realitzen múltiples apostes en un quadrat. (En el cas més senzill, com es pot observar, només una de les 1055 és per a guanyar).
En el nou joc BONO-LOTO les probabilitats són 4 vegades majors, ja que una mateixa aposta participa en 4 sortejos. Seran les següents:

(En el cas més senzill, de 263 apostes, només hi ha una possibilitat).
Sorteig de cecs
En el sorteig de l'ONCE només hi ha 5 premis. Participen 100.000 números. La probabilitat d'obtenir el Premi Principal és de 1/10 5, és a dir, 0,00001. La probabilitat d'obtenir el segon premi (però no el primer) és de 9/10 5 = 0,00009. La tercera (i no les dos anteriors) s'obté amb una probabilitat de 9/10 4 = 0,9. Per a obtenir el quart (i no els anteriors) la probabilitat és de 9/10 3 = 0,009 i finalment la probabilitat d'aconseguir només el cinquè és de 9/10 2 = 0,09. (Si s'aconsegueix un premi, cal tenir en compte que no es poden aconseguir premis inferiors) Però la probabilitat d'obtenir almenys un premi és de 1/10 = 0,1 (això correspon a encertar l'última xifra).
Fins ara hem dit el relatiu a les probabilitats de jocs d'atzar coneguts. Com es veu, no és fàcil aconseguir diners amb aquests mètodes.
Cadena d'or
Ara, i com prometia, parlarem de l'augment del nombre de persones que participen en el joc de la Cadena d'Or i dels grans números.
Suposem que una persona necessita una setmana per a vendre dues llistes. En l'Estat es preveu que la compra de la llista sigui de 20.000.000 d'habitants. Com es pot observar en el següent llistat, en la setmana 23, 8.388.608 comprarien una llista, quedant 3.222.786 persones sense llista, veure taula original. La setmana següent caldria vendre 16.777.216 llistes. Si ens assegurem que cada persona compra una sola llista, no quedarien amics per a comprar totes les llistes. És a dir,
S'ha utilitzat una llista per a indicar. Però és sorprenent saber que prenent la meitat de la població mundial, és a dir, 2.000 milions de persones, el joc acabaria en la setmana 29 (és a dir, només 6 setmanes després), com es pot veure en la següent llista.
Per a acabar
Agafa ara un paper i no diguis més o menys quantes vegades pots doblegar. Prova-ho amb un foli. Ho has aconseguit? Que no? Agafa una pàgina més gran, per exemple la doble pàgina del periòdic i torna a intentar-lo. Quantes vegades ha doblegat? Suposem que el gruix d'una fulla és de 0,001 cm.
Si pleguem la fulla una vegada obtenim el gruix de dues fulles. Tornant a doblegar, el gruix de les quatre fulles i de seguir així, plegant-les en 50 vegades obtindríem el gruix de 2 50 = 1.125.699.906.842.624 fulles, és a dir:

és a dir, més d'onze milions de quilòmetres de gruix. En la pràctica s'ha demostrat que es pot plegar fins a 8 vegades. Si parlem de números grans, farem dues preguntes per a acabar l'article: quant trigaria a comptar un milió de números partint d'1 (un, dos, ...)? i comptar un bilió? (Calcula els números que comptes en un minut).