Cadena de oro y...
El juego que ha creado muchos rumores en los últimos tiempos es la cadena de oro. Ya se ha dicho mucho sobre este juego en medios de comunicación, televisión, periódicos, radio. Nosotros aquí relacionaremos este juego con las matemáticas.
Empecemos por el desarrollo del juego y veamos cómo se pueden ganar 40.960.000 pesetas. Suponemos que la persona A compra una lista. Una vez adquirida la lista, deberá abonar a la primera persona que aparezca en ella 5.000 pesetas. Como pagó otras 5.000 pesetas por la lista, de momento ha perdido 10.000 pesetas. Ahora tiene que quitar el primer nombre de la lista y el suyo en el lugar 12, es decir, escribir.
Esta nueva lista deberá ser vendida a dos personas. Si estos dos son B y C, estos tendrán en su lista el nombre de A en 12º lugar (en este momento A recupera 10.000 pesetas, por lo que no ha perdido nada). Las personas B y C deben pasar las listas a otras dos personas, como D, E, F y G. En las listas de estas cuatro personas encontraríamos el nombre de A en el puesto 11. En el siguiente paso 8 serán las personas que tengan el nombre de A en 10º lugar en la lista. La próxima vez 16 personas tendrán el nombre de A en la 9ª plaza. No es difícil estimar que el número de personas que tienen el nombre de A en 1ª posición es 4.096.
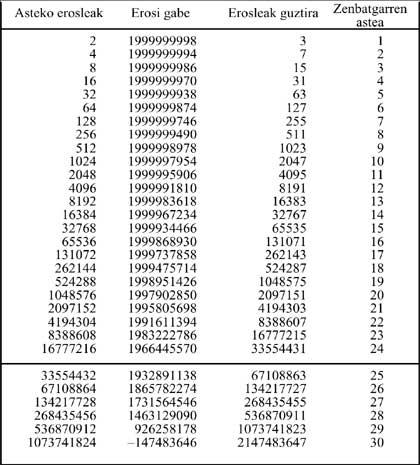
Estos últimos deben vender las listas a 8.192 personas, en todas estas listas el nombre de A está en 1ª posición. Por lo tanto, estas 8.192 personas tendrán que pagar a A cinco mil pesetas para comprar la lista, es decir, A debería cobrar 8.192 x 5.000 = 40.960.00 pesetas (si todo sale bien). A la espera de seguir mejor lo expuesto, se adjunta la tabla con todos los pasos del proceso:

Hasta aquí hemos hecho una descripción del juego. En esta descripción se observa un importante incremento del número de personas. Al final del artículo hablaremos de esto y de grandes números. Aquí hemos mencionado las palabras juego y dinero, y ahora nos resulta difícil no mencionar otros juegos de azar que conocemos para ganar dinero rápido.
En esta ocasión vamos a proceder al cálculo aproximado de las probabilidades de estos juegos.
No podemos considerar la cadena de oro como un juego de azar. ¿Cuál es la probabilidad de vender una lista? Yo conozco a un amigo que ha vendido las dos listas un día, pero también a un amigo que ha pasado dos semanas y no ha vendido ninguna lista. No hablamos, por tanto, de la probabilidad de este juego, pero sí de los demás.
Quinielas
Para empezar, por qué no, analizaremos las quinielas. Por supuesto, en este juego el factor humano tiene su importancia, no lo negaremos (1, X, 2 no tienen la misma probabilidad de salir en los partidos Real-Sabadell o Osasuna-Atletia de Bilbao).
Pero desde el punto de vista de la persona que hace la apuesta, a cada partido le podríamos poner 1, X o 2, acertando sólo con uno, es decir, la probabilidad de acertar será de 1/3. Probabilidad de adivinar dos partidos 1/3 . 1/3 (primera y segunda). Por lo tanto, sería la probabilidad de acertar los 14 partidos (todo ello con una columna por supuesto).

Con dos o tres símbolos aumentará la probabilidad. La mayor apuesta múltiple es de 5 triples y 2 dobles. Esto supone 972 apuestas. Por lo tanto, en este caso la probabilidad es de 0,0002032 (es decir, de 4.921 apuestas sólo una posibilidad). Como se puede observar, aunque se ha avanzado mucho, no se ha alcanzado la décima parte, y la cantidad a gastar es de 19.440 pesetas (no analizaremos aquí los desarrollos abreviados).
Seguiremos con la lotería. El factor humano no influye en este juego. Hay muchos premios en la lotería, pero el mayor sólo corresponde a uno de los 80.000 números. Probabilidad en este caso
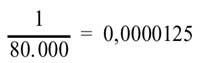
es, bajo en absoluto. Hay un premio llamado pedrea (como todos sabemos, si la última cifra de tu número coincide con el premio principal, te devuelven lo que juegas). Teniendo en cuenta que en un sorteo ordinario hay aproximadamente 1.200 premios (sin contar los finales), la probabilidad de conseguir un premio es de 0,015 (es decir, sólo una de cada 67 probabilidades), no está mal comparada con el quiniela.
Loto
El sistema de sorteo del loto es totalmente diferente. El jugador deberá elegir 6 del 49. Las probabilidades de ser premiado se presentan en la siguiente tabla.

Aquí no analizaremos los casos en los que se realizan múltiples apuestas en un cuadrado. (En el caso más sencillo, como se puede observar, sólo una de las 1055 es para ganar).
En el nuevo juego BONO-LOTO las probabilidades son 4 veces mayores, ya que una misma apuesta participa en 4 sorteos. Serán las siguientes:

(En el caso más sencillo, de 263 apuestas, sólo hay una posibilidad).
Sorteo de ciegos
En el sorteo de la ONCE sólo hay 5 premios. Participan 100.000 números. La probabilidad de obtener el Premio Principal es de 1/10 5, es decir, 0,00001. La probabilidad de obtener el segundo premio (pero no el primero) es de 9/10 5 = 0,00009. La tercera (y no las dos anteriores) se obtiene con una probabilidad de 9/10 4 = 0,9. Para obtener el cuarto (y no los anteriores) la probabilidad es de 9/10 3 = 0,009 y por último la probabilidad de alcanzar sólo el quinto es de 9/10 2 = 0,09. (Si se consigue un premio, hay que tener en cuenta que no se pueden conseguir premios inferiores) Pero la probabilidad de obtener al menos un premio es de 1/10 = 0,1 (esto corresponde a acertar la última cifra).
Hasta ahora hemos dicho lo relativo a las probabilidades de juegos de azar conocidos. Como se ve, no es fácil conseguir dinero con estos métodos.
Cadena de oro
Ahora, y como prometía, vamos a hablar del aumento del número de personas que participan en el juego de la Cadena de Oro y de los grandes números.
Supongamos que una persona necesita una semana para vender dos listas. En el Estado se prevé que la compra de la lista sea de 20.000.000 de habitantes. Como se puede observar en el siguiente listado, en la semana 23, 8.388.608 comprarían una lista, quedando 3.222.786 personas sin lista, ver tabla original. La semana siguiente habría que vender 16.777.216 listas. Si nos aseguramos de que cada persona compra una sola lista, no quedarían amigos para comprar todas las listas. Es decir,
Se ha utilizado una lista para indicar. Pero es sorprendente saber que tomando la mitad de la población mundial, es decir, 2.000 millones de personas, el juego terminaría en la semana 29 (es decir, sólo 6 semanas después), como se puede ver en la siguiente lista.
Para terminar
Coge ahora un papel y no digas más o menos cuántas veces puedes doblar. Pruébalo con un folio. ¿Lo has conseguido? ¿Que no? Coge una página más grande, por ejemplo la doble página del periódico y vuelve a intentarlo. ¿Cuántas veces ha doblado? Supongamos que el espesor de una hoja es de 0,001 cm. Si plegamos la hoja una vez obtenemos el espesor de dos hojas. Volviendo a doblar, el grosor de las cuatro hojas y de seguir así, plegándolas en 50 veces obtendríamos el espesor de 2 50 = 1.125.699.906.842.624 hojas, es decir:

es decir, más de once millones de kilómetros de espesor. En la práctica se ha demostrado que se puede plegar hasta 8 veces. Si hablamos de números grandes, vamos a hacer dos preguntas para terminar el artículo: ¿cuánto tardaría en contar un millón de números partiendo de 1 (uno, dos, ...)? ¿y contar un billón? (Calcula los números que cuentas en un minuto).