Gold chain and...
The game that has created many rumors in recent times is the gold chain. Much has already been said about this game in media, television, newspapers, radio. We here will relate this game to mathematics.
Let's start with the game development and see how you can win 40,960.000 pesetas. We assume that person A buys a list. Once you have purchased the list, you must pay the first person to show 5,000 pesetas. As he paid another 5,000 pesetas for the list, so far he has lost 10,000 pesetas. Now you have to remove the first name from the list and yours in place 12, i.e. write.
This new list must be sold to two people. If these two are B and C, these will have in their list the name of A in 12th place (at this time A recovers 10,000 pesetas, so it has not lost anything). People B and C must pass the lists to two other people, such as D, E, F and G. In the lists of these four people we would find the name A in 11th place. In the next step 8 will be the people who have the name of A in 10th place in the list. Next time 16 people will be named A in 9th place. It is not difficult to estimate that the number of people who have the name of A in 1st position is 4,096.
The latter must sell the lists to 8,192 people, in all these lists the name of A is in 1st position. Therefore, these 8,192 people will have to pay A five thousand pesetas to buy the list, that is, A should charge 8.192 x 5,000 = 40.960.00 pesetas (if everything goes well). Waiting to better follow the above, the table with all the steps of the process is attached:

So far we have made a description of the game. This description shows a significant increase in the number of people. At the end of the article we will talk about this and big numbers. Here we have mentioned the words game and money, and now we find it difficult not to mention other gambling that we know to make fast money.
This time we will proceed to the approximate calculation of the odds of these games.
We cannot consider the gold chain as a game of chance. What is the probability of selling a list? I know a friend who has sold the two lists one day, but also a friend who has spent two weeks and has not sold any lists. We do not speak, therefore, of the probability of this game, but of the others.
Quinielas
To begin with, why not, we will analyze the quinelas. Of course, in this game the human factor has its importance, we will not deny it (1, X, 2 do not have the same probability of going out in the matches Real-Sabadell or Osasuna-Atletia of Bilbao).
But from the point of view of the person who makes the bet, we could put each match 1, X or 2, just with one, that is, the probability of success will be 1/3. Probability of guessing two matches 1/3 . 1/3 (first and second). Therefore, it would be the probability to hit the 14 matches (all with a column of course).

With two or three symbols it will increase the probability. The biggest multiple bet is 5 triples and 2 doubles. This means 972 bets. Therefore, in this case the probability is 0.0002032 (i.e. 4,921 bets only one possibility). As can be seen, although much progress has been made, the tenth part has not been reached, and the amount to be spent is 19,440 pesetas (we will not analyze abbreviated developments here).
We will continue with the lottery. The human factor does not influence this game. There are many prizes in the lottery, but the biggest is only one of the 80,000 numbers. Probability in this case
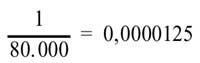
is, low at all. There is a prize called pedrea (as we all know, if the last number of your number matches the main prize, you get back what you play). Considering that in an ordinary draw there are approximately 1,200 prizes (not counting the finals), the probability of getting a prize is 0.015 (that is, only one out of every 67 odds), it is not bad compared to the five.
Lotus
The lotus draw system is totally different. The player must choose 6 from 49. The odds of being awarded are presented in the table below.

Here we will not analyze cases where multiple bets are placed on a square. (In the simplest case, as you can see, only one of the 1055 is to win.)
In the new game BONO-LOTO the odds are 4 times higher, since the same bet participates in 4 draws. They will be as follows:

(In the simplest case, of 263 bets, there is only one possibility).
Blind Draw
In the ONCE draw there are only 5 prizes. 100,000 numbers participate. The probability of obtaining the Main Prize is 1/10 5, i.e. 0.00001. The probability of winning the second prize (but not the first) is 9/10 5 = 0.00009. The third (and not the previous two) is obtained with a probability of 9/10 4 = 0.9. To get the fourth (and not the previous ones) the probability is 9/10 3 = 0.009 and finally the probability of reaching only the fifth is 9/10 2 = 0.09. (If you get a prize, you have to keep in mind that you cannot get lower prizes) But the probability of obtaining at least one prize is 1/10 = 0.1 (this corresponds to matching the last figure).
So far we have said about the known odds of gambling. As you can see, it is not easy to get money with these methods.
Gold Chain
Now, and as I promised, let's talk about the increase in the number of people participating in the Gold Chain game and the big numbers.
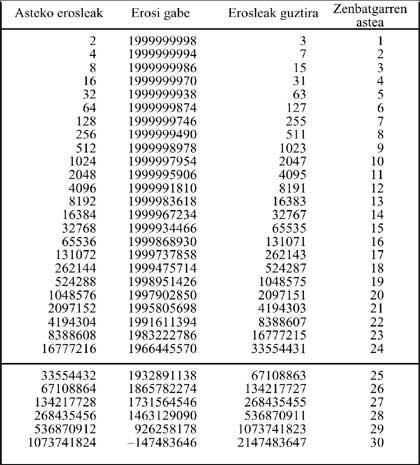
Suppose a person needs a week to sell two lists. In the State, the purchase of the list is expected to be 20,000,000 inhabitants. As can be seen in the following list, in week 23, 8,388,608 would buy a list, leaving 3,222,786 people without list, see original table. The following week would have to sell 16,777,216 lists. If we make sure that each person buys a single list, there would be no friends left to buy all lists. That is,
A list has been used to indicate. But it is surprising to know that taking half of the world's population, that is, 2 billion people, the game would end at week 29 (that is, only 6 weeks later), as you can see in the following list.
To finish
Take a paper now and don't say more or less how many times you can fold. Try it with a foil. Have you got it? What not? Take a larger page, for example the double page of the newspaper and try again. How many times have you folded? Suppose the thickness of a sheet is 0.001 cm.
If we fold the sheet once we get the thickness of two sheets. Bending back, the thickness of the four leaves and continuing like this, folding them in 50 times we would obtain the thickness of 2 50 = 1.125.699.906.842.624 sheets, that is:

that is, more than eleven million kilometers thick. In practice it has been shown that it can be folded up to 8 times. If we talk about big numbers, we will ask two questions to finish the article: how long would it take to count a million numbers starting from 1 (one, two, ..)? and count a billion? (Calculate the numbers you count in a minute.)