pi, constante circular
O matemático William Oughtred era un home pequeno, de ollo negro. Deitaba moi tarde, normalmente durmía tentando resolver algún problema. Cando circulaba pola rúa, a cabeza traballaba e de cando en vez paraba e debuxaba no po do chan os diagramas matemáticos. En 1647 ocorréuselle que paira realizar algúns cálculos de círculos utilizásese a letra grega.

Oughtred non utilizou na relación entre o diámetro e a circunferencia en cambio. Pero así se coñece hoxe en día e sería un traballo inútil cambiar iso. A propia constante matemática é máis antiga que a expresión. O que sabemos é que desde que o ser humano preocupouse das matemáticas, coñecemos o número en. E é que, comezando polos babilonios, os geometristas quixeron medir o seu valor exacto.
Na actualidade asignouse esta función a computadores xigantes. Con todo, a reputación do número© estendeuse fóra do ambiente matemático.
Esta constante utilizouse durante 2.500 anos, moitas veces sen valor específico. Na Biblia, o primeiro libro dos Reyes e o segundo das Crónicas, descríbese a construción do templo de Salomón. Entre outras, ofrécense medidas concretas do gran depósito de auga denominada Mar de Bronce, de 10 brazos de diámetro e de 30 brazos de corda (ou perímetro). Desta descrición dedúcese que o número amarre amparado polo amante da memoria daba o valor "3". Outros pobos déronlle un valor máis concreto. Os exipcios e algunhas culturas mesopotámicas outorgábanlle valores de 3,125 e 3,162, respectivamente. Estes valores poden asociarse con 25/8 e 10 operacións.
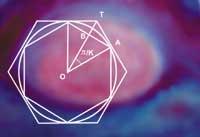
Con todo, os gregos Arquímedes de Siracusa (a.C.) 287-212) deixounos o primeiro método escrito paira o calco teórico do n. Trátase dun cálculo sobre unha circunferencia de radio determinado. Por unha banda, inscribiu no interior da circunferencia un polígono regular e, por outro, circunscribiuno dentro doutro polígono maior de igual número de lados. Ao aumentar o número de lados dos polígonos, ao aproximarse ao infinito, os perímetros exteriores e interiores son iguais, a lonxitude da circunferencia.
Coa aplicación deste método, Arquímedes non sacou ningún valor concreto, pero logrou una boa aproximación. Alcanzou o polígono da zona 96 e determinou que o número en g debía estar comprendido entre os valores 223/71 e 22/7 (entre 3,1408 e 3,1429 aproximadamente). A media entre ambos é de 3,1418, que difire 0,0002 do valor actualmente coñecido.
É un esforzo reseñable, xa que Arquímedes non dispuña da nosa notación matemática actual nin de ferramentas avanzadas. Outros levaron a mesma metodoloxía máis adiante. O dominio da ciencia moveuse aos poucos cara ao leste. A seguinte achega teórica chegou da man do matemático Tsu Ch'ung Chi (430-501). Seguramente non coñecía Arquímedes. Con todo, o resultado das estimacións foi de 3,1416, valor que consideramos válido paira moitas operacións.
En Occidente
Próximas referencias europeas XVII. dependentes. O máis coñecido desta época é o proposto polo matemático escocés James Gregory (1638-1675) (aínda que ás veces o matemático Gottfried Wilhelm von Leibniz sexa considerado autor):
6.5/4 = 1 - 1/3 + 1/5 - 1/7 + …
Tratábase de metodoloxías de orixe xeométrica, pero cun marcado carácter matemático moderno. No entanto, a medida que se engaden os termos o erro aumenta considerablemente. Con fórmulas similares, algunhas matemáticas introduciron moitas horas no cálculo dos decimais do número©. O matemático inglés William Shanks (1812-1882) obtivo 707 decimais, dos cales só 527 eran correctos.
O alemán Carl Louis Ferdinand von Lindemann (1852-1939) demostrou que tamén é transcendente, é dicir, que non é a solución dun polinomio con números enteiros.
Época dos circuítos
XX. A mediados do século XX introducíronse os computadores na historia do número©. F. O inglés Ferguson calculou 808 decimais en 1947 mediante un programa informático. Dous anos despois chegou aos 2.000 decimais. A partir de aí, tanto os algoritmos como as calculadoras (computadores) melloraron moito e, por tanto, o coñecido número de decimais aumentou considerablemente. Por exemplo, os matemáticos David Bailey, Peter Borwein e Simon Plouffe, sen necesidade de decimais anteriores, desenvolveron a fórmula paira calcular calquera decimal.
En 1999 eran 68.719.470.000 decimais, pero a competencia continúa. Neste sentido, os matemáticos expoñen cuestións case filosóficas. Cantas veces aparece una cifra? Hai grandes secuencias repetitivas? Cal é realmente a natureza do número en...?
A verdade da mentira estatística

XVIII. O matemático francés Georges Buffon do século XX descubriu o teorema binomial. Este matemático, con todo, lémbrase polo método de cálculo estatístico do n. Curioso! A modo de grella debuxou liñas no chan e ademais aleatoriamente lanzou palitos da metade da distancia entre filas. Contaba un punto cada vez que queda cruzado sobre a liña. Dividindo o número de puntos de 25 tiros por 100 permite una aproximación ao n. Con este método, Lazzerini obtivo en 1901 3.1415929 resultados.





