pi, constante circulaire
Le mathématicien William Oughtred était un petit homme à œil noir. Il couchait très tard, dormait normalement en essayant de résoudre un problème. Quand elle circulait dans la rue, la tête travaillait et parfois arrêtait et dessinait dans la poussière du sol les diagrammes mathématiques. En 1647, il a pensé que pour effectuer des calculs de cercles, on utilisait la lettre grecque.

Oughtred n'a pas employé dans le rapport entre le diamètre et la circonférence au lieu. Mais on le connaît aujourd'hui et ce serait un travail inutile de changer cela. La constante mathématique elle-même est plus ancienne que l'expression. Ce que nous savons, c'est que depuis que l'être humain se souciait des mathématiques, nous avons connu le nombre. Et c'est que, à commencer par les Babyloniens, les géométriciens ont voulu mesurer leur valeur exacte.
Cette fonction a été actuellement assignée à des ordinateurs géants. Cependant, la réputation du nombre© s'est étendue hors de l'environnement mathématique.
Cette constante a été utilisée pendant 2.500 ans, souvent sans valeur spécifique. Dans la Bible, le premier livre des Rois et le second des Chroniques, décrit la construction du temple de Salomon. Entre autres, des mesures concrètes sont proposées pour le grand réservoir d'eau appelé Mer de Bronze, de 10 bras de diamètre et de 30 bras de corde (ou périmètre). De cette description on déduit que le nombre amarré protégé par l'amant de la mémoire donnait la valeur "3". D'autres peuples lui ont donné une valeur plus concrète. Les Égyptiens et certaines cultures mésopotamiennes lui donnaient respectivement des valeurs de 3,125 et 3,162. Ces valeurs peuvent être associées à 25/8 et 10 opérations.
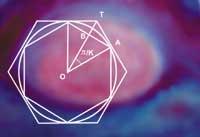
Cependant, les Grecs Archimède de Syracuse (a.C.) 287-212) nous a laissé la première méthode écrite pour le calque théorique du n. Il s'agit d'un calcul sur une circonférence de rayon déterminée. D'une part, il inscrivit à l'intérieur de la circonférence un polygone régulier et, d'autre part, il le circonscrit à l'intérieur d'un autre polygone plus grand que le nombre de côtés. En augmentant le nombre de côtés des polygones, en s'approchant de l'infini, les périmètres extérieurs et intérieurs sont égaux, la longueur de la circonférence.
Avec l'application de cette méthode, Archimède n'a pas tiré aucune valeur concrète, mais a obtenu une bonne approximation. Il atteignit le polygone de la zone 96 et détermina que le nombre en g devait être compris entre les valeurs 223/71 et 22/7 (entre 3 1408 et 3 1429 environ). La moyenne entre les deux est de 3,1418, qui diffère 0,0002 de la valeur actuellement connue.
C'est un effort remarquable, car Archimède ne disposait ni de notre notation mathématique actuelle ni d'outils avancés. D'autres ont apporté la même méthodologie plus tard. La domination de la science s'est déplacée lentement vers l'est. La contribution théorique suivante est venu de la main du mathématicien Tsu Ch'ung Chi (430-501). Je ne connaissais sûrement pas Archimède. Cependant, le résultat des estimations était de 3,1416, valeur que nous considérons valable pour de nombreuses opérations.
En Occident
Prochaines références européennes XVII. dépendants. Le plus connu de cette époque est celui proposé par le mathématicien écossais James Gregory (1638-1675) (bien que parfois le mathématicien Gottfried Wilhelm von Leibniz soit considéré comme un auteur):
6.5/4 = 1 - 1/3 + 1/5 - 1/7 + …
Il s'agissait de méthodologies d'origine géométrique, mais avec un caractère mathématique moderne. Cependant, comme les termes sont ajoutés, l'erreur augmente considérablement. Avec des formules semblables, quelques mathématiques ont introduit beaucoup d'heures dans le calcul des nombres décimaux©. Le mathématicien anglais William Shanks (1812-1882) a obtenu 707 décimales, dont seulement 527 étaient corrects.
L'Allemand Carl Louis Ferdinand von Lindemann (1852-1939) a démontré qu'il est également transcendant, c'est-à-dire qu'il n'est pas la solution d'un polynôme avec des nombres entiers.
Temps des circuits
XX. Au milieu du XXe siècle, les ordinateurs ont été introduits dans l'histoire du nombre©. F. L'anglais Ferguson a calculé 808 décimales en 1947 par logiciel. Deux ans plus tard, il est arrivé à 2000 décimales. À partir de là, les algorithmes et les calculatrices (ordinateurs) ont beaucoup progressé et le nombre de décimales a donc considérablement augmenté. Par exemple, les mathématiciens David Bailey, Peter Borwein et Simon Plouffe, sans avoir besoin de décimales antérieures, ont développé la formule pour calculer n'importe quelle décimale.
En 1999 ils étaient 68.719.470.000 décimaux, mais la concurrence continue. En ce sens, les mathématiciens soulèvent des questions presque philosophiques. Combien de fois un chiffre apparaît? Y a-t-il de grandes séquences répétitives ? Quelle est vraiment la nature du nombre dans... ?
La vérité du mensonge statistique

XVIII. Le mathématicien français Georges Buffon du XXe siècle a découvert le théorème binomial. Ce mathématicien, cependant, est rappelé par la méthode de calcul statistique du n. Curieux ! En guise de grille, il dessina des lignes sur le sol et lança aléatoirement des bâtonnets de la moitié de la distance entre les rangées. Il comptait un point chaque fois qu'il est croisé sur la ligne. En divisant le nombre de points de 25 coups par 100 permet une approximation au n. Avec cette méthode, Lazzerini a obtenu en 1901 3.1415929 résultats.





