pi, constant circular
El matemàtic William Oughtred era un home petit, d'ull negre. Ficava al llit molt tard, normalment dormia intentant resoldre algun problema. Quan circulava pel carrer, el cap treballava i de tant en tant parava i dibuixava en la pols del sòl els diagrames matemàtics. En 1647 se li va ocórrer que per a realitzar alguns càlculs de cercles s'utilitzés la lletra grega.

Oughtred no va utilitzar en la relació entre el diàmetre i la circumferència en canvi. Però així es coneix avui dia i seria un treball inútil canviar això. La pròpia constant matemàtica és més antiga que l'expressió. El que sabem és que des que l'ésser humà es va preocupar de les matemàtiques, hem conegut el número en. I és que, començant pels babilonis, els geometristas han volgut mesurar el seu valor exacte.
En l'actualitat s'ha assignat aquesta funció a ordinadors gegants. No obstant això, la reputació del número© s'ha estès fora de l'ambient matemàtic.
Aquesta constant s'ha utilitzat durant 2.500 anys, moltes vegades sense valor específic. En la Bíblia, el primer llibre dels Reis i el segon de les Cròniques, es descriu la construcció del temple de Salomó. Entre altres, s'ofereixen mesures concretes del gran dipòsit d'aigua denominat Mar de Bronze, de 10 braços de diàmetre i de 30 braços de corda (o perímetre). D'aquesta descripció es dedueix que el número amarrament emparat per l'amant de la memòria donava el valor "3". Altres pobles li van donar un valor més concret. Els egipcis i algunes cultures mesopotàmiques li atorgaven valors de 3,125 i 3,162, respectivament. Aquests valors poden associar-se amb 25/8 i 10 operacions.
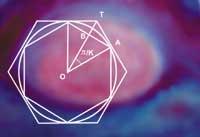
No obstant això, els grecs Arquimedes de Siracusa (a. C.) 287-212) ens va deixar el primer mètode escrit per al calc teòric del n. Es tracta d'un càlcul sobre una circumferència de radi determinat. D'una banda, va inscriure a l'interior de la circumferència un polígon regular i, per un altre, el va circumscriure dins d'un altre polígon major d'igual nombre de costats. En augmentar el nombre de costats dels polígons, en aproximar-se a l'infinit, els perímetres exteriors i interiors són iguals, la longitud de la circumferència.
Amb l'aplicació d'aquest mètode, Arquimedes no va treure cap valor concret, però va aconseguir una bona aproximació. Va aconseguir el polígon de la zona 96 i va determinar que el número en g havia d'estar comprès entre els valors 223/71 i 22/7 (entre 3,1408 i 3,1429 aproximadament). La mitjana entre tots dos és de 3,1418, que difereix 0,0002 del valor actualment conegut.
És un esforç ressenyable, ja que Arquimedes no disposava de la nostra notació matemàtica actual ni d'eines avançades. Uns altres van portar la mateixa metodologia més endavant. El domini de la ciència es va moure a poc a poc cap a l'est. La següent aportació teòrica va arribar de la mà del matemàtic Tsu Ch'ung Chi (430-501). Segurament no coneixia Arquimedes. No obstant això, el resultat de les estimacions va ser de 3,1416, valor que considerem vàlid per a moltes operacions.
A Occident
Pròximes referències europees XVII. dependents. El més conegut d'aquesta època és el proposat pel matemàtic escocès James Gregory (1638-1675) (encara que a vegades el matemàtic Gottfried Wilhelm von Leibniz sigui considerat autor):
6.5/4 = 1 - 1/3 + 1/5 - 1/7 + …
Es tractava de metodologies d'origen geomètric, però amb un marcat caràcter matemàtic modern. No obstant això, a mesura que s'afegeixen els termes l'error augmenta considerablement. Amb fórmules similars, algunes matemàtiques van introduir moltes hores en el càlcul dels decimals del número©. El matemàtic anglès William Shanks (1812-1882) va obtenir 707 decimals, dels quals només 527 eren correctes.
L'alemany Carl Louis Ferdinand von Lindemann (1852-1939) va demostrar que també és transcendent, és a dir, que no és la solució d'un polinomi amb nombres enters.
Època dels circuits
XX. A mitjan segle XX es van introduir els ordinadors en la història del número©. F. L'anglès Ferguson va calcular 808 decimals en 1947 mitjançant un programa informàtic. Dos anys després va arribar als 2.000 decimals. A partir d'aquí, tant els algorismes com les calculadores (ordinadors) han millorat molt i, per tant, el conegut nombre de decimals ha augmentat considerablement. Per exemple, els matemàtics David Bailey, Peter Borwein i Simon Plouffe, sense necessitat de decimals anteriors, van desenvolupar la fórmula per a calcular qualsevol decimal.
En 1999 eren 68.719.470.000 decimals, però la competència continua. En aquest sentit, els matemàtics plantegen qüestions gairebé filosòfiques. Quantes vegades apareix una xifra? Hi ha grans seqüències repetitives? Quin és realment la naturalesa del número en...?
La veritat de la mentida estadística

XVIII. El matemàtic francès Georges Buffon del segle XX va descobrir el teorema binomial. Aquest matemàtic, no obstant això, es recorda pel mètode de càlcul estadístic del n. Curiós! A manera de graella va dibuixar línies en el sòl i a més aleatòriament va llançar palitos de la meitat de la distància entre files. Comptava un punt cada vegada que queda travessat sobre la línia. Dividint el nombre de punts de 25 tirs per 100 permet una aproximació al n. Amb aquest mètode, Lazzerini va obtenir en 1901 3.1415929 resultats.





