pi, constant circular
Mathematician William Oughtred was a small, black-eyed man. I lay very late, normally slept trying to solve some problem. When it circulated on the street, the head worked and occasionally stopped and drew mathematical diagrams in the dust of the ground. In 1647 it occurred to him that to make some calculations of circles the Greek letter was used.

Oughtred did not use in the relationship between diameter and circumference instead. But this is known today and it would be useless to change that. The mathematical constant itself is older than expression. What we know is that since the human being cared about mathematics, we have known the number in. Beginning with the Babylonians, the geometrists wanted to measure their exact value.
This function has now been assigned to giant computers. However, the reputation of the number© has spread outside the mathematical environment.
This constant has been used for 2,500 years, often without specific value. In the Bible, the first book of Kings and the second book of Chronicles describes the construction of the temple of Solomon. Among others, concrete measures are offered of the large water tank called the Bronze Sea, with 10 arms in diameter and 30 arms of rope (or perimeter). From this description it follows that the mooring number protected by the lover of memory gave the value "3". Other peoples gave it more concrete value. Egyptians and some Mesopotamian cultures gave it values of 3,125 and 3,162, respectively. These values can be associated with 25/8 and 10 operations.
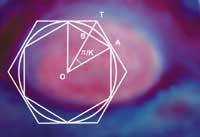
However, the Greek Archimedes of Syracuse (BC) 287-212) left us the first written method for the theoretical calc of n. This is a calculation of a given radius circumference. On the one hand, a regular polygon was inscribed inside the circumference and, on the other, it was circumscribed within another polygon larger than the same number of sides. By increasing the number of sides of the polygons, by approaching infinity, the outer and inner perimeters are equal, the length of the circumference.
With the application of this method, Archimedes did not draw any concrete value, but achieved a good approximation. It reached the polygon of zone 96 and determined that the number in g should be between values 223/71 and 22/7 (between 3,1408 and 3,1429 approximately). The mean between the two is 3,1418, which differs 0.0002 from the currently known value.
It is a remarkable effort, since Archimedes did not have our current mathematical notation or advanced tools. Others took the same methodology later. The domain of science gradually moved to the east. The next theoretical contribution came from the hand of mathematician Tsu Ch'ung Chi (430-501). Surely I did not know Archimedes. However, the result of the estimates was 3,1416, which we consider valid for many operations.
In the West
Next European references XVII. dependents. The best known of this time is the one proposed by the Scottish mathematician James Gregory (1638-1675) (although sometimes the mathematician Gottfried Wilhelm von Leibniz is considered author):
6.5/4 = 1 - 1/3 + 1/5 - 1/7 + …
These were methodologies of geometric origin, but with a marked modern mathematical character. However, as the terms are added the error increases considerably. With similar formulas, some mathematics introduced many hours in the calculation of the decimals of the number©. The English mathematician William Shanks (1812-1882) obtained 707 decimals, of which only 527 were correct.
The German Carl Louis Ferdinand von Lindemann (1852-1939) proved that it is also transcendent, that is, that it is not the solution of a polynomial with integers.
Time of the circuits
XX. In the middle of the 20th century computers were introduced in the history of the number©. F. English Ferguson calculated 808 decimal places in 1947 using a computer program. Two years later it reached 2,000 decimals. From there, both algorithms and calculators (computers) have improved a lot and, therefore, the well-known number of decimals has increased considerably. For example, mathematicians David Bailey, Peter Borwein and Simon Plouffe, without the need for previous decimals, developed the formula for calculating any decimal.
In 1999 there were 68,719,470.000 decimals, but the competition continues. In this sense, mathematicians raise almost philosophical questions. How many times does a figure appear? Are there large repetitive sequences? What is really the nature of the number in...?
The truth of the statistical lie

XVIII. French mathematician Georges Buffon of the 20th century discovered binomial theorem. This mathematician, however, is remembered by the method of statistical calculation of n. Curious! As a grid he drew lines on the ground and also randomly threw sticks of half the distance between rows. He counted one point each time he crossed over the line. Dividing the number of points of 25 shots per 100 allows an approximation to n. With this method, Lazzerini obtained in 1901 3,1415929 results.





