Agujas, número pi y longitud de las curvas

XVIII. En el siglo XVIII el conde de Buffon era responsable del Jardín Real de París y poco a poco escribió sus veinticinco tomos de su “Histoire Naturelle”. En esa historia pensaba hacer una recopilación sistemática de todos los seres vivos y creía que el ser humano debía ser su lugar. El principal rasgo de los seres humanos es el miedo a la muerte, según Buffon, pero no sabemos cómo decidió que otros animales no tienen ese miedo. El segundo rasgo, y lo que a nosotros nos importa aquí, es la pasión por el juego y a eso dedicó el apartado “Essai d’Arithmétique morale”
En los juegos se jugaba dinero, por supuesto, y tenemos que conocer nuestra probabilidad de ganar para que el juego sea limpio. Para poner un ejemplo, supongamos que al lanzar un dato nos posicionamos a favor de que aparezca el número “5”. Si ganamos, nos deben entregar el dinero jugado seis veces, ya que la probabilidad es de 1/6. Por el contrario, si nos posicionamos a favor de la aparición de un número ba-coiti, sólo recibiremos el doble del dinero jugado, porque ahora la probabilidad es 1/2. Para calcular la probabilidad, contamos los casos posibles (seis en nuestro ejemplo) y los favorables (uno en el caso del “5”, tres en el caso de los impares) y dividimos este último entre el primero.
Buffon propuso un juego geométrico en el que el cálculo de la probabilidad no se podía realizar contando casos. El “problema de la aguja de Buffon” consiste en realizar unas rectas paralelas en el suelo, fijando la distancia (d) entre ellas y lanzando una aguja de l. de longitud entre ellas, siendo l d. El que hace una postura a favor de que la aguja corte una línea, ¿cuánto tiene que recibir? Como se ha indicado anteriormente, es necesario conocer la probabilidad de este suceso y concretamente se obtiene 2 l / d (cuadro de visión). Por ejemplo, si la distancia entre líneas es de 5 cm y la aguja mide 3 cm, la probabilidad es de 0,38197 y por cada peseta jugada habría que cobrar 2,618 al acierto.
No sabemos si este juego se ha utilizado alguna vez para ganar (o perder) monedas, pero Laplace en su libro “ Théorie analytique des Probabilités ” (1812) encontró una aplicación curiosa que le acercaba al valor de p. Para ello, tras tirar la aguja entre varias líneas, dividiendo el número de veces que corta una línea por el número total de veces que hemos echado, el valor aproximado de la probabilidad es tanto más fiable cuanto más se esté actuando. El valor obtenido puede ser liberado por 2 l / d iguales. Los resultados que aparecen en la literatura son demasiado buenos para ser creíbles, pero hay que tener en cuenta que el que estaba haciendo el experimento ya sabía el resultado que quería conseguir y cuando le convenía se paraba. Si el valor de se desconoce realmente, con los tiros que se citan en torno a los 5000 el segundo decimal sería incierto.
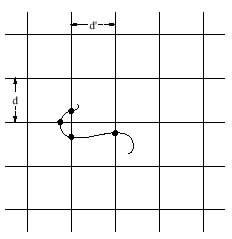
Puede proponerse algunas modificaciones de este problema y Laplace propuso una formulación más general: el plano se divide ahora en cuadros, con rectas paralelas horizontales a una distancia d’ y verticales a una distancia d’, y entre ellas se lanza un hilo de longitud l, de cualquier forma (no necesariamente directa como la aguja). El hilo puede cortar la red de líneas en varios puntos y la esperanza matemática del número de puntos de corte es:
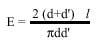
Es decir, si tras el lanzamiento N el número medio de puntos de corte es E(N), cuando N va hacia el infinito, E(N) va hacia el valor de E superior. Como se puede observar, cuando d’ va hacia el infinito se obtiene el resultado de la antigua aguja de Buffon. Y una vez más, conociendo d, d’ y l, esta fórmula se puede utilizar para acercarse al número.
Si no resulta interesante para el cálculo de esta vía, en esta nueva formulación existe un valor que puede ser realmente desconocido, es decir, la longitud del hilo. Y parece que en la práctica también se ha utilizado. Si miramos al microscopio, es posible que algunas de las longitudes que aparecen en él no puedan medirse. No podemos tirar el “hilo” al plano cuadri-culto, pero podemos proyectar sobre la imagen del microscopio una malla cuadriculada (conociendo las diferencias) y contar los puntos de corte, girar la red y volver a contar los cortes hasta completar la gira. El número medio de cortes nos da un valor aproximado de la E superior y con su fórmula se obtiene la longitud, lógicamente porque conocemos el valor de.
La parte de las Matemáticas que estudia estos problemas y otros similares se llama “Probabilidad Geométrica”. El primer volumen de la colección “Integral Geometry and Geometric Probability” (“Encyclopedia of Mathematics and its Applications”, Addison-Wesley, 1976) de Santaló descubrirá cosas interesantes sobre este tema. En el prólogo del libro, el prestigioso matemático Mark Kac califica al profesor Santaló como “el jefe indiscutible de Geometría Integral durante muchos años”.






