Hasiera »   Erreportajeak »   Orratzak, pi zenbakia eta kurben luzera

Needles, number pi and length of curves

• Zabaldu:
• Twitter
• Facebook
• Emaila

Luis Antonio Santaló Sors was born in Girona in 1911. Student of Rey Pastor and Blaschke, Ph.D. in Madrid and was professor at the Escuela Aeronáutica de la República in Cartagena during the war. After the war he moved to Argentina, where he was professor of Rosario, La Plata and Buenos Aires. In those years Argentina brought together a large group of mathematicians, internationally renowned, of which Mr. Santaló was an important part. In 1983 he received the “Prince of Asturias” award. Last October, at the meeting of mathematicians organized by the “Argentine Mathematical Union”, the closing conference itself, from school teachers to university professors, the public of different levels was fascinated by the paths taken by Santaló’s master’s degree. The following lines reflect part of this conference.

XVIII. In the eighteenth century the count of Buffon was responsible for the Royal Garden of Paris and gradually wrote his twenty-five volumes of his “Histoire Naturelle”. In that story I was thinking of making a systematic collection of all living things and believed that the human being should be his place. The main trait of human beings is the fear of death, according to Buffon, but we do not know how he decided that other animals do not have that fear. The second trait, and what we care about here, is the passion for the game and to that he dedicated the section “Essai d’Arithmétique morale”

In the games money was played, of course, and we have to know our probability of winning to make the game clean. To give an example, let’s assume that when launching a data we position ourselves in favor of the number “5” appearing. If we win, we must deliver the money played six times, since the probability is 1/6. On the contrary, if we position ourselves in favor of the appearance of a ba-coiti number, we will only receive twice the money played, because now the probability is 1/2. To calculate the probability, we count the possible cases (six in our example) and the favorable ones (one in the case of “5”, three in the case of the odd ones) and divide the latter among the first.

Buffon proposed a geometric game in which the calculation of probability could not be performed by counting cases. The “problem of the Buffon needle” consists of performing parallel straight lines on the ground, setting the distance (d) between them and throwing a needle of l. length between them, being l d. The one who makes a position in favor of the needle cutting a line, how much does he have to receive? As indicated above, it is necessary to know the probability of this event and specifically you get 2 l / d (vision box). For example, if the distance between lines is 5 cm and the needle measures 3 cm, the probability is 0.38197 and for each peseta played we would have to charge 2,618 to success.

We do not know if this game has ever been used to win (or lose) coins, but Laplace in his book “Théorie analytique des Probabilités” (1812) found a curious application that approached the p value. To do this, after pulling the needle between several lines, dividing the number of times you cut a line by the total number of times you cast, the approximate value of the probability is all the more reliable the more you are acting. The value obtained can be released by 2 l/d equal. The results that appear in the literature are too good to be credible, but it must be borne in mind that the one who was doing the experiment already knew the result he wanted to achieve and when it suited him stood. If the value of is not really known, with the shots cited around 5000 the second decimal would be uncertain.

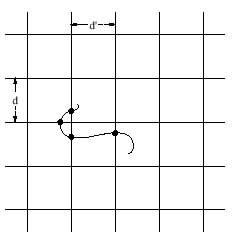
Some modifications of this problem can be proposed and Laplace proposed a more general formulation: the plane is now divided into squares, with horizontal parallel lines at a distance d’ and vertical at a distance d’, and between them a thread of length l, in any form (not necessarily direct as the needle) is thrown. The thread can cut the line network into several points and the mathematical hope of the number of cutoff points is:

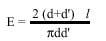
That is, if after launch N the average number of cutoff points is E(N), when N goes towards infinity, E(N) goes towards the higher E value. As you can see, when d’ goes towards infinity you get the result of the old Buffon needle. And once again, knowing d, d’ and l, this formula can be used to approach the number.

If it is not interesting for the calculation of this path, in this new formulation there is a value that can be really unknown, that is, the length of the thread. And it seems that in practice it has also been used. If we look under a microscope, some of the lengths that appear in it may not be measured. We can’t pull the “thread” into the quad-cult plane, but we can project on the microscope image a grid grid (knowing the differences) and count the cut-off points, rotate the grid and recount the cuts until the tour is completed. The average number of cuts gives us an approximate value of the upper E and with its formula the length is obtained, logically because we know the value of.

The part of mathematics that studies these and similar problems is called “Geometric Probability.” The first volume of the collection “Integral Geometry and Geometric Probability” (“Encyclopedia of Mathematics and its Applications”, Addison-Wesley, 1976) by Santaló will discover interesting things about this subject. In the book’s foreword, the prestigious mathematician Mark Kac calls Professor Santaló “the undisputed head of Integral Geometry for many years.”