Agulles, número pi i longitud de les corbes

XVIII. En el segle XVIII el comte de Buffon era responsable del Jardí Real de París i a poc a poc va escriure els seus vint-i-cinc toms del seu “Histoire Naturelle”. En aquesta història pensava fer una recopilació sistemàtica de tots els éssers vius i creia que l'ésser humà havia de ser el seu lloc. El principal tret dels éssers humans és la por a la mort, segons Buffon, però no sabem com va decidir que altres animals no tenen aquesta por. El segon tret, i el que a nosaltres ens importa aquí, és la passió pel joc i a això va dedicar l'apartat “Essai d’Arithmétique morale”
En els jocs es jugava diners, per descomptat, i hem de conèixer la nostra probabilitat de guanyar perquè el joc sigui net. Per a posar un exemple, suposem que en llançar una dada ens posicionem a favor que aparegui el número “5”. Si guanyem, ens han de lliurar els diners jugats sis vegades, ja que la probabilitat és de 1/6. Per contra, si ens posicionem a favor de l'aparició d'un número ba-coiti, només rebrem el doble dels diners jugats, perquè ara la probabilitat és 1/2. Per a calcular la probabilitat, comptem els casos possibles (sis en el nostre exemple) i els favorables (un en el cas del “5”, tres en el cas dels imparells) i dividim aquest últim entre el primer.
Buffon va proposar un joc geomètric en el qual el càlcul de la probabilitat no es podia realitzar comptant casos. El “problema de l'agulla de Buffon” consisteix a realitzar unes rectes paral·leles en el sòl, fixant la distància (d) entre elles i llançant una agulla de l. de longitud entre elles, sent l d. El que fa una postura a favor que l'agulla talli una línia, quant ha de rebre? Com s'ha indicat anteriorment, és necessari conèixer la probabilitat d'aquest succés i concretament s'obté 2 l / d (quadre de visió). Per exemple, si la distància entre línies és de 5 cm i l'agulla mesura 3 cm, la probabilitat és de 0,38197 i per cada pesseta jugada caldria cobrar 2,618 a l'encert.
No sabem si aquest joc s'ha utilitzat alguna vegada per a guanyar (o perdre) monedes, però Laplace en el seu llibre “ Théorie analytique donis Probabilités ” (1812) va trobar una aplicació curiosa que li acostava al valor de p. Per a això, després de tirar l'agulla entre diverses línies, dividint el nombre de vegades que talla una línia pel nombre total de vegades que hem tirat, el valor aproximat de la probabilitat és tant més fiable com més s'estigui actuant. El valor obtingut pot ser alliberat per 2 l / d iguals. Els resultats que apareixen en la literatura són massa bons per a ser creïbles, però cal tenir en compte que el que estava fent l'experiment ja sabia el resultat que volia aconseguir i quan li convenia es parava. Si el valor des desconeix realment, amb els tirs que se citen entorn dels 5000 el segon decimal seria incert.
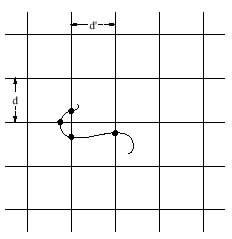
Pot proposar-se algunes modificacions d'aquest problema i Laplace va proposar una formulació més general: el pla es divideix ara en quadres, amb rectes paral·leles horitzontals a una distància d’ i verticals a una distància d’, i entre elles es llança un fil de longitud l, de qualsevol forma (no necessàriament directa com l'agulla). El fil pot tallar la xarxa de línies en diversos punts i l'esperança matemàtica del nombre de punts de tall és:
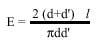
És a dir, si després del llançament N el nombre mitjà de punts de tall és E(N), quan N va cap a l'infinit, E(N) va cap al valor de E superior. Com es pot observar, quan d’ va cap a l'infinit s'obté el resultat de l'antiga agulla de Buffon. I una vegada més, coneixent d, d’ i l, aquesta fórmula es pot utilitzar per a acostar-se al número.
Si no resulta interessant per al càlcul d'aquesta via, en aquesta nova formulació existeix un valor que pot ser realment desconegut, és a dir, la longitud del fil. I sembla que en la pràctica també s'ha utilitzat. Si mirem al microscopi, és possible que algunes de les longituds que apareixen en ell no puguin mesurar-se. No podem tirar el “fil” al pla cuadri-culte, però podem projectar sobre la imatge del microscopi una malla quadriculada (coneixent les diferències) i comptar els punts de tall, girar la xarxa i tornar a comptar els talls fins a completar la gira. El nombre mitjà de corts ens dóna un valor aproximat de la E superior i amb la seva fórmula s'obté la longitud, lògicament perquè coneixem el valor de.
La part de les Matemàtiques que estudia aquests problemes i uns altres similars es diu “Probabilitat Geomètrica”. El primer volum de la col·lecció “Integral Geometry and Geometric Probability” (“Encyclopedia of Mathematics and its Applications”, Addison-Wesley, 1976) de Santaló descobrirà coses interessants sobre aquest tema. En el pròleg del llibre, el prestigiós matemàtic Mark Kac qualifica al professor Santaló com “el cap indiscutible de Geometria Integral durant molts anys”.






