Désordre
Commençons donc par le test suivant:
1. Trois points d'une sphère sont choisis au hasard. Quelle est la probabilité que les trois points soient dans le même hémisphère ? (On peut considérer que les points que le cercle maximum délimitant l'hémisphère, par exemple l'équateur, a à l'intérieur, appartiennent à l'un des deux hémisphères).
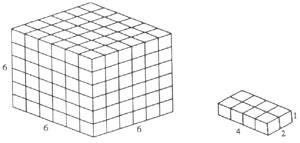
2. Peut-on compléter un cube de 6x6x6 avec vingt briques de 1x2x4 dimensions ? (Voir figure 1).
3. Un logique, qui devait passer du temps dans une ville, a décidé d'aller à un salon de coiffure. Dans la ville il y avait seulement deux salons de coiffure. Il s'est adressé à l'un d'eux. Là, il a vu des choses désordonnées: le propriétaire portait des vêtements sales, avait une barbe de quelques jours et les cheveux brisés. Il ne tarda pas à déménager. À cette occasion, tout était bien ordonné. Élégant coiffeur sans barbes et bien peigné. Logiquement, rien d'autre que le voir, il est revenu à la première. Pourquoi ?
4ème Regardez les cinq images de poxpoker (Figure 2).
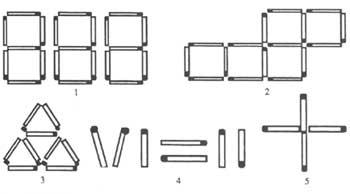
1. En enlevant neuf poxpoles, il en laisse six.
2. En changeant deux poxpoles de pièce, laissez les cinq carrés par quatre (tous les poxpoles doivent être quelque part d'un carré).
3. En éliminant quatre, trois ou deux poxpoles de cette image, on peut obtenir deux triangles équilatéraux. Comment ?
4° Réalisez cette égalité en déplaçant un seul poxpolu.
5. Complétez un carré en déplaçant une seule poche sur cette croix. (Il ne sert pas à déplacer une paire de millimètres un poxpule pour que les quatre extrémités forment un carré vide)
5. Supposons que nous ayons six boules de la même taille : deux rouges, deux noires et deux blanches. Dans chaque couple une boule est plus lourde que l'autre. Les trois boules lourdes ont le même poids et les trois légères aussi. En ne faisant que deux poids avec une balance, comment pouvez-vous différencier le pesé dans chaque couple?
6º Voici (Figure 3) les nombres. Sur ces 7 x 8 rectangles sont dispersés vingt-huit dominos. Pour voir si vous les trouvez (celle de gauche a une solution unique, l'autre a huit solutions différentes et c'est pourquoi c'est plus difficile).
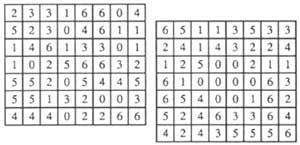
7. Un éleveur a 20 porcs, 40 vaches et 60 chevaux. Mais si nous appelons les vaches aux chevaux, combien de vaches aura-t-il ?
8º. Construisez huit triangles équilatéraux en dessinant six droites de la même longueur.
9. Prenez dix pièces. Avec ces dix pièces, vous devez former cinq lignes droites de quatre pièces.
10. Dessinez une ligne droite et prenez trois pièces. Placez ces trois pièces pour qu'elles restent deux faces d'un côté de la ligne et deux croix entières à l'autre.
11. Si un fer semblable au «beignet» est mis à chauffer, le diamètre du trou augmentera-t-il ou diminuera-t-il?
12. Quel est le plus grand nombre que vous pouvez écrire en mettant seulement 2 chiffres trois fois?
13. Nous avons fait un tour complet du grand cercle que l'on voit dans la figure 4. Par conséquent, la longueur de votre circonférence sera PQ. Dans le même temps, nous avons fait un tour du cercle intérieur, étant la longueur de sa circonférence RS. Comment expliquer pourquoi les longueurs de ces deux circonférences étaient égales ?

14. Le crétane Epimenides a dit : tous les crétois sont des menteurs. Que pouvez-vous dire de cette phrase?
15. Protagoras fait un pacte avec son élève. Selon l'accord, l'élève devait payer les études quand il a gagné son premier cas. À la fin de l'élève n'a pas eu de chance et n'a pas trouvé de clients pendant une longue période. Protagore, inquiet, a dénoncé son étudiant. Protagoras a fait valoir dans le procès que si je gagne le procès, je devrais payer pour purger la peine. Au contraire, si vous gagnez, je dois payer selon notre accord. Par conséquent, je dois payer en tout cas. Mais l'élève n'était pas d'accord et lui répondit: si tu gagnes, en respectant notre alliance, tu n'auras pas à payer et si je gagne, les juges ne m'obligeront pas à payer. Donc, en aucun cas, je dois payer. Quel est le bon raisonnement?
16. Avec le cheval d'échecs remplissez les carrés suivants sans passer deux fois par case. (Figure 5).

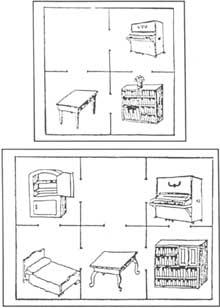
17. Voici deux problèmes de traduction. Dans les deux cas, il est supposé que seul un meuble est introduit dans chaque pièce et dans les deux cas les propriétaires veulent déplacer le piano et la bibliothèque, en passant le piano à la salle où se trouve la bibliothèque et vice versa. Comment devraient-ils agir avec les moindres changements possibles? (Figure 6).
18. Trois bandes blanches et deux bandes noires sont enseignées aux amis A, B et C. Puis accrochez un ruban sur le dos de chacun. Chaque personne peut voir les bandes des autres, mais pas la sienne. Chacun doit deviner quelle couleur il porte dans le dos. Son ami A voit que les bandes des autres sont blanches. Après quelques minutes sans que personne ne dise, A a donné la bonne réponse. Quelle est la réponse et comment avez-vous raisonné?
19. Un commerçant a quatre pièces ou poids. Avec ces poids, vous pouvez effectuer tous les poids de 1 à 40 kg. par kilo. Quel poids avez-vous?
20. Dis, aigu, trois nombres dont les produits et sommes sont égaux.
21. Bittori et Itziar veulent prendre le train des onze. L'horloge de Bittori est retardée de 10 minutes, mais il croit qu'il est en avance de 5 minutes. L'horloge d'Itziar, en revanche, est 5 minutes en avance, mais il croit que 10 minutes est retardée. Quel sera le premier arrêt?
22. Dans une bibliothèque, située de gauche à droite, il y a trois livres. Le premier se compose de 340 pages, le second de 400 et le troisième de 350. Une pipe commence à être mangée de la première page du premier exemplaire à la dernière de la troisième. Combien de feuilles passera la carcome ?
23. Cimetière ou épitaphe de Diophante: Il raconte Diophante avec la tombe dans laquelle apparaissent les différentes étapes de sa vie: dans son enfance, il donna la sixième partie de sa vie; à partir de là, la doceava part jusqu'à ce que la barbe a commencé à remplir les joues; à partir de là, la septième, jusqu'à ce qu'elle se marie; cinq ans après son mariage son fils est né; puis, quand il est arrivé à la moitié de l'âge de son père, il est mort imprévisible; son père. Donc, vous pouvez imaginer votre âge.
24. Prenez cinq pièces. Placez trois faces vers le haut et les deux autres avec la croix vers le haut (AGAGA). Vous devez obtenir de laisser les trois faces d'un côté et les croix de l'autre (AAAGG ou GGAAA). Pour cela, vous devez toujours déplacer deux pièces: une face et l'autre croix (AG ou GA). (Le creux qui reste après un mouvement ne peut pas être rempli par l'union des pièces de monnaie, c'est à dire si AGAGAGAÆA_ _GAGA est fait alors A F AGAGA, mais AAGG_ _A).
25. La boule qui est dans un sac peut être blanche ou noire. Une boule blanche a été mise sur le sac et une boule blanche a été retirée. Quelle est la probabilité que la balle qui reste dans le sac soit blanche quand elle sort? (Lewis Carroll).
26. Dans un sac, il y a plusieurs boules noires et blanches (au moins une de chacune). Les boules sortiront comme suit: vous prenez une boule, votre couleur est vissée et rejetée. Si une deuxième boule sort et est de la couleur de la précédente, elle sera écartée. Il prendra la troisième, si elle redevient de la même couleur sera jeté et ainsi de suite jusqu'à ce que vous obtenez une boule d'une autre couleur. Lorsque vous sortez une boule différente, mettez dans le sac et une fois agitée, l'extraction sera reprise. Par exemple :
Noir à la 1ère sortie: Jeter en 2ème sortie le noir: jeter en 3ème sortie le blanc: mettre en sac
Blanc à la sortie 4: jeter à la sortie 5 le noir: mettre dans le sac
Blanc à la sortie 6 : jeter à la sortie 7 le blanc : jeter à la sortie 8 le noir : mettre dans le sac
Peu importe la situation initiale. La dernière balle qui reste dans le sac a la même probabilité d'être noire. Quelle est cette probabilité?





