Desorden
Comencemos por lo tanto con el siguiente test:
1. Se eligen al azar tres puntos de una esfera. ¿Cuál es la probabilidad de que los tres puntos estén en el mismo hemisferio? (Se puede considerar que los puntos que el círculo máximo que delimita el hemisferio, por ejemplo el ecuador, tiene en su interior, pertenecen a cualquiera de los dos hemisferios).
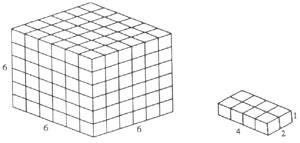
2. ¿Se puede completar un cubo de 6x6x6 con veinte ladrillos de 1x2x4 dimensiones? (Ver figura 1).
3. Un lógico, que tenía que pasar el tiempo en una ciudad, decidió ir a una peluquería. En la ciudad sólo había dos peluquerías. Se dirigió a uno de ellos. Allí vio cosas desordenadas: el propio propietario llevaba ropa sucia, tenía una barba de unos días y el pelo destrozado. No tardó en trasladarse. En esta ocasión todo estaba bien ordenado. Elegante peluquero sin barbas y bien peinado. Lógico, nada más verlo, volvió a la primera. ¿Por qué?
4º Observa las cinco imágenes de poxpóker (figura 2).
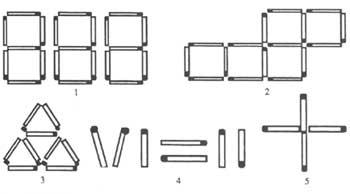
1. Quitando nueve poxpolos, deja seis.
2. Cambiando dos poxpolos de sitio, deja los cinco cuadrados por cuatro (todos los poxpolos deben estar en algún lado de un cuadrado).
3. Eliminando cuatro, tres o dos poxpolos de esta imagen, se pueden obtener dos triángulos equiláteros. ¿Cómo?
4º Haz realidad esa igualdad moviendo un solo poxpolu.
5. Completa un cuadrado moviendo un solo poche en esta cruz. (No sirve mover un par de milímetros un poxpulo para que los cuatro extremos formen un cuadrado vacío)
5. Supongamos que tenemos seis bolas del mismo tamaño: dos rojas, dos negras y dos blancas. En cada pareja una bola es más pesada que la otra. Las tres bolas pesadas tienen el mismo peso y las tres ligeras también. Haciendo solo dos pesos con una balanza, ¿cómo se puede diferenciar el pesado en cada pareja?
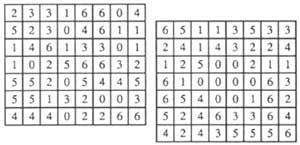
6º He ahí (Figura 3) los dámeros numéricos. En estos 7 x 8 rectángulos se encuentran dispersas veintiocho fichas de dominó. A ver si las encuentras (la de la izquierda tiene una única solución, la otra tiene ocho soluciones diferentes y por eso es más difícil).
7. Un ganadero tiene 20 cerdos, 40 vacas y 60 caballos. Pero si llamamos vacas a los caballos, ¿cuántas vacas tendrá?
8º. Construye ocho triángulos equiláteros dibujando seis rectas de la misma longitud.
9. Toma diez monedas. Con estas diez monedas tienes que formar cinco líneas rectas de cuatro monedas.
10. Dibuja una línea recta y coge tres monedas. Coloca estas tres monedas para que queden dos caras a un lado de la línea y dos cruces enteras a otro.
11. Si un hierro similar al “donuts” se pone a calentar, ¿aumentará o disminuirá el diámetro del agujero?
12. ¿Cuál es el número más grande que se puede escribir poniendo sólo 2 cifras tres veces?
13. Hemos dado una vuelta completa al gran círculo que se ve en la figura 4. Por tanto, la longitud de su circunferencia será PQ. Al mismo tiempo hemos dado una vuelta al círculo interior, siendo la longitud de su circunferencia RS. ¿Cómo explicaría la razón de que las longitudes de estas dos circunferencias fueran iguales?

14. El cretano Epimenides dijo: todos los cretenses son mentirosos. ¿Qué puedes decir de esta frase?
15. Protágoras hizo un pacto con un alumno suyo. Según el acuerdo, el alumno tenía que pagar los estudios cuando ganó su primer caso. Al finalizar el alumno no tuvo suerte y no encontró clientes durante mucho tiempo. Protágoras, preocupado, denunció a su estudiante. Protágoras argumentó en el juicio que si yo gano el pleito me tendría que pagar para cumplir la sentencia. Por el contrario, si ganas, me tendré que pagar según nuestro acuerdo. Por lo tanto, me tendré que pagar en cualquier caso. Pero el alumno no estaba de acuerdo y le contestó: si ganas tú, respetando nuestro pacto no tendrás que pagar y si gano yo, los jueces no me obligarán a pagar. Por lo que en ningún caso debo pagar. ¿Cuál es el razonamiento correcto?
16. Con el caballo de ajedrez rellena los siguientes cuadrados sin pasar dos veces por cada casilla. (Figura 5).

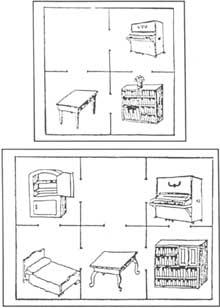
17. A continuación se presentan dos problemas de traslación. En ambos casos se supone que sólo se introduce un mueble en cada habitación y en ambos casos los dueños quieren trasladar el piano y la biblioteca, pasando el piano a la sala donde está la biblioteca y viceversa. ¿Cómo deberán actuar con los menores cambios posibles? (Figura 6).
18. A los amigos A, B y C se les enseñan tres cintas blancas y dos cintas negras. Luego cuelga una cinta en la espalda de cada uno. Cada persona puede ver las cintas de los demás, pero no la suya. Cada uno debe adivinar qué color lleva en la espalda. Su amigo A ve que las cintas de los demás son blancas. Pasados unos minutos sin que nadie dijera, A dio la respuesta correcta. ¿Cuál es la respuesta y cómo la razonó?
19. Un comerciante tiene cuatro piezas o pesos. Con estos pesos se pueden realizar todas las pesadas de 1 a 40 kg. por kilo. ¿Qué pesos tiene?
20. Di, agudo, tres números cuyos productos y sumas son iguales.
21. Bittori e Itziar quieren coger el tren de los once. El reloj de Bittori está retrasado 10 minutos, pero él cree que está adelantado 5 minutos. El reloj de Itziar, en cambio, está 5 minutos adelantado, pero él cree que 10 minutos está retrasado. ¿Cuál llegará a la primera parada?
22. En una biblioteca, situada de izquierda a derecha, hay tres libros. El primero consta de 340 páginas, el segundo de 400 y el tercero de 350. Una pipa comienza a comerse desde la primera página del primer ejemplar hasta la última de la tercera. ¿Cuántas hojas atravesará la carcoma?
23. Cementerio o epitafio de Diofanto: Cuenta Diofanto con la tumba en la que aparecen las distintas etapas de su vida: en su infancia dio la sexta parte de su vida; a partir de ahí, la doceava parte hasta que la barba empezó a llenar las mejillas; a partir de entonces, la séptima, hasta que se casó; cinco años después de su matrimonio nació su hijo; después, cuando llegó a la mitad de la edad de su padre, murió imprevisiblemente; su padre lloró cuatro veranos. De ahí que puedas imaginar su edad.
24. Coge cinco monedas. Coloca tres caras hacia arriba y las otras dos con la cruz hacia arriba (AGAGA). Tienes que conseguir dejar las tres caras a un lado y las cruces a otro (AAAGG o GGAAA). Para ello siempre tienes que mover dos monedas: una cara y la otra cruz (AG o GA). (El hueco que queda después de un movimiento no se puede llenar mediante la unión de monedas, es decir, si se hace AGAGAÆA_ _GAGA, no se puede hacer luego A F AGAGA, pero sí AAGG_ _A).
25. La bola que está en una bolsa puede ser blanca o negra. Se ha metido una bola blanca a la bolsa y tras sacarla se ha sacado una bola que es blanca. ¿Cuál es la probabilidad de que la bola que queda en la bolsa sea blanca cuando sale? (Lewis Carroll).
26. En una bolsa hay varias bolas blancas y negras (al menos una de cada una). Las bolas saldrán de la siguiente manera: se coge una bola, se apunta su color y se rechaza. Si sale una segunda bola y es del color de la anterior, se descartará. Se tomará la tercera, si vuelve a ser del mismo color se descartará y así sucesivamente hasta conseguir una bola de otro color. Cuando salga una bola diferente, se mete en la bolsa y una vez agitada se retomará la extracción. Por ejemplo:
Negro en 1ª salida: Desechar en 2ª salida el negro: desechar en 3ª salida el blanco: meter en bolsa
Blanco en la salida 4: desechar en la salida 5 el negro: meter en la bolsa
Blanco en la salida 6: desechar en la salida 7 el blanco: desechar en la salida 8 el negro: meter en la bolsa
No importa la situación inicial. La última bola que queda en la bolsa tiene la misma probabilidad de ser negra. ¿Cuál es esa probabilidad?





