Disorder of Order
Let us therefore begin with the following test:
1. Three points of a sphere are randomly chosen. What is the probability that the three points will be in the same hemisphere? (It can be considered that the points that the maximum circle delimiting the hemisphere, for example the equator, has inside, belong to either of the two hemispheres).
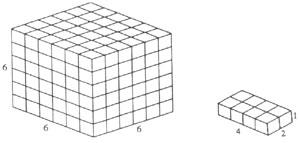
2. Can a 6x6x6 cube be completed with twenty 1x2x4 dimensions bricks? (See figure 1).
3. A logical, who had to spend time in a city, decided to go to a hairdresser. In the city there were only two hairdressers. He addressed one of them. There he saw disordered things: the owner himself wore dirty clothes, had a beard of a few days and shattered hair. It did not take long to move. On this occasion everything was well ordered. Elegant hairdresser without beards and well combed. Logical, just to see him, he returned to the first. Why?
4º See the five images of poxpoker (Figure 2).
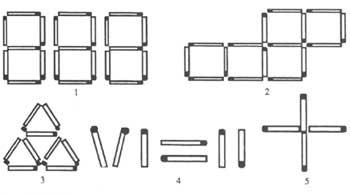
1. Removing nine poxpoles, leaves six.
2. Changing two poxpoles of site, leave the five squares for four (all poxpoles must be somewhere in a square).
3. By removing four, three or two poxpoles from this image, two equilateral triangles can be obtained. How?
4th Realize that equality by moving a single poxpolu.
5. Complete a square by moving a single pot on this cross. (It is not useful to move a couple of millimeters a poxpulo so that the four ends form an empty square)
5. Suppose we have six balls of the same size: two red, two black and two white. In each pair a ball is heavier than the other. The three heavy balls have the same weight and the three light also. Making only two pesos with a balance, how can you differentiate the heavy in each couple?
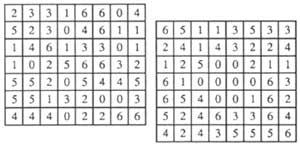
6º Here (Figure 3) the numerical numbers. In these 7 x 8 rectangles are dispersed twenty-eight dominoes. To see if you find them (the left has a single solution, the other has eight different solutions and that is why it is more difficult).
7. A rancher has 20 pigs, 40 cows and 60 horses. But if we call horses cows, how many cows will it have?
8º. Build eight equilateral triangles by drawing six straight lines of the same length.
9. Take ten coins. With these ten coins you have to form five straight lines of four coins.
10. Draw a straight line and take three coins. Place these three coins so that they remain two faces on one side of the line and two whole crosses on the other.
11. If an iron-like “donuts” is put to heat, will the hole diameter increase or decrease?
12. What is the largest number that can be written by putting only 2 figures three times?
13. We have taken a complete turn to the great circle seen in figure 4. Therefore, the length of its circumference will be PQ. At the same time we have turned the inner circle, being the length of its circumference RS. How would you explain the reason that the lengths of these two circles were equal?

14. The Epimenides cretan said: all cretans are liars. What can you say about this phrase?
15. Protágoras made a pact with a student of his. According to the agreement, the student had to pay for the studies when he won his first case. At the end the student was not lucky and did not find clients for a long time. Protágoras, concerned, denounced his student. Protágoras argued in the trial that if I win the lawsuit I would have to pay to comply with the judgment. On the contrary, if you win, I will have to pay according to our agreement. Therefore, I will have to pay in any case. But the student did not agree and answered him: if you win, respecting our covenant you will not have to pay and if I win, the judges will not force me to pay. So in no case should I pay. What is the correct reasoning?
16. With the chess horse fill the following squares without spending twice for each square. (Figure 5).

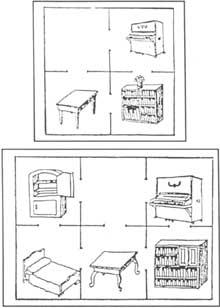
17. Below are two translation problems. In both cases it is assumed that only one piece of furniture is introduced in each room and in both cases the owners want to transfer the piano and the library, passing the piano to the room where the library is and vice versa. How should they act with the smallest possible changes? (Figure 6).
18. Friends A, B and C are taught three white ribbons and two black ribbons. Then hang a tape on the back of each one. Each person can see the tapes of others, but not theirs. Everyone should guess what color it carries on the back. His friend A sees that the ribbons of others are white. After a few minutes without anyone saying, A gave the correct answer. What is the answer and how did you reason it?
19. A trader has four pieces or pesos. With these weights can be carried out all weighing from 1 to 40 kg. by kilo. What weights does it have?
20. Di, sharp, three numbers whose products and sums are equal.
21. Bittori and Itziar want to catch the eleven train. The Bittori watch is delayed 10 minutes, but he believes it is advanced 5 minutes. The Itziar clock, however, is 5 minutes ahead, but he believes that 10 minutes is delayed. What will arrive at the first stop?
22. In a library, located from left to right, there are three books. The first consists of 340 pages, the second of 400 and the third of 350. A pipe begins to be eaten from the first page of the first specimen to the last of the third. How many leaves will cross the carcoma?
23. Cemetery or epitaph of Diofanto: Diophanto counts with the tomb in which appear the different stages of his life: in his childhood he gave the sixth part of his life; from there, the twelfth part until the beard began to fill the cheeks; from then on, the seventh, until he married; five years after his marriage his son was born; then, when he arrived at the half of his father's age, he died unpredictably; his father wept. Hence you can imagine his age.
24. Take five coins. Place three faces upwards and the other two with the cross upwards (AGAGA). You have to get to leave the three faces to one side and crosses to another (AAAGG or GGAAA). For this you always have to move two coins: one face and the other cross (AG or GA). (The gap that is left after a move cannot be filled by the union of coins, that is, if AGAGAÆA_ _GAGA is made, then A F AGAGA, but yes AAGG_ _A).
25. The ball in a bag can be white or black. A white ball has been put into the bag and, after pulling it out, a ball has been drawn that is white. What is the probability that the remaining ball in the bag will be white when it comes out? (Lewis Carroll).
26. In a bag there are several white and black balls (at least one of each). The balls will come out as follows: take a ball, aim its color and refuse. If a second ball comes out and is the color of the previous one, it will be discarded. It will take the third, if it returns to be of the same color will be discarded and so on until getting a ball of another color. When a different ball comes out, he gets into the bag and once agitated the extraction will be retaken. For example:
Black on 1st exit: Discard in 2nd exit the black: discard in 3rd exit the white: put in bag
White at exit 4: discard at exit 5 the black: put in the bag
White at exit 6: discard at exit 7 the white: discard at exit 8 the black: put in the bag
No matter the initial situation. The last remaining ball in the bag has the same probability of being black. What is that probability?





