Mesturado (II)
Con motivo das vacacións quixemos traer a este número un novo revolto. Á espera de que estes días teñas tempo, preparamos 50 cuestionarios para que poidas encher esta beta. Como na anterior, aquí tamén podes atopar de todo: a lúa, a vaca, os poxpolos, os cadrados, as divisións, os soños, as gansos, os ollos, os rectos, ........................................................................................................................................................................................................... En xeral, si non son de broma, non te fíes, pódesche marear.
1. Si a persoa fose invisible, veríao?
O ollo que che traes non é
porque o ves ti, é
porque veche o ollo.
(Antonio Machado)
2. Una persoa ve o oso e desprázase cara ao sur correndo 10 km. Desde alí percorreu outros 10 km ao leste e, finalmente, outros 10 km ao norte. Mira onde e o mesmo oso volve velo. De que cor é o oso?
3. Temos oito moedas aparentemente iguais, pero una ten menos peso que outras. Pódese saber cal é a moeda facendo só dous pesos?
4º Que signo hai que pór no recuadro baleiro? (Figura 1)

5. Producíase nun pobo situado na fronteira entre os estados de Ibaibusti e Mendiberdea. Una libra de Ibaibusti custaba 90 céntimos dunha libra de Mendiberdea. Así mesmo, una libra de Mendiberde a 90 céntimos dunha libra de Ibaibusti. Un día, una persoa entrou nun bar da zona de Ibaibusti e pediu un zume de 10 céntimos pagou cunha libra local. Ao seu regreso, en lugar de doar 90 céntimos de Ibaibusti, déronlle una libra de Mendiber-d. Máis tarde trasladouse a un bar de Mendiberde e cando pediu unha vimbia de 10 céntimos pagou con libéraa anterior, devolvendo 90 céntimos a unha libera de Ibaibusti. Desta forma desprazouse unha e outra vez dun bar a outro. Por último, tras beber todo o que se quería, volveu a casa co diñeiro que tiña ao principio. Quen pagou as vimbias?
6º Pon en tres pilas 11, 7 e 6 moedas. En tres movementos debes deixar oito moedas en tres cheas. Nos movementos, a cada pila pódeselle engadir tantas moedas como teña e estas moedas deben proceder do mesma chea.
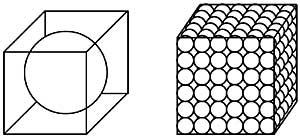
7. Temos dúas caixas cúbicas iguais. Nun deles hai una bóla de ferro de diámetro igual á altura da caixa; no outro, como se ve na imaxe, hai as mesmas bólas de ferro. Que caixa ten máis peso? (Figura 2)
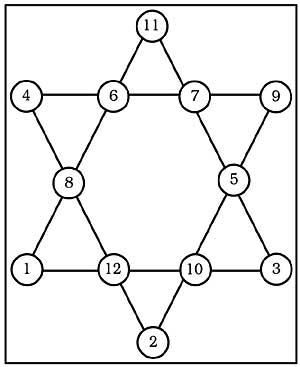
8º. A estrela da figura 3 é máxica, xa que a suma dos catro números das súas seis liñas son 26. Con todo, a suma dos números dos seus vértices é de 30. Podería solucionalo paira conseguir una superestrella máxica, é dicir, que a suma dos vértices tamén sexa 26?
9. Como se pode solucionar o seguinte produto que está mal sen engadir, quitar ou escribir nada?
81. 9 = 801
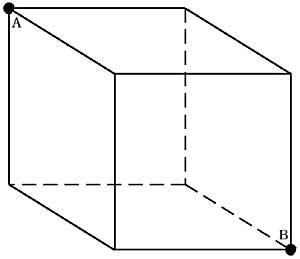
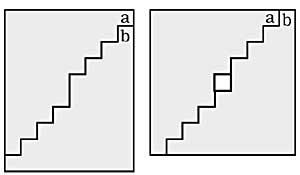
10. Cal é a ruta máis curta paira pasar da a B por encima da superficie do cubo? (Figura 4)
11. Este suceso tivo lugar nun pobo inglés, na mañá e na igrexa dun domingo. O sacerdote traballaba no seu sermón, como sempre. O sol queimaba. Debido ao silencio que había no seu interior e ao rumor afastado da rúa, Peter se dormió. En tempos da revolución francesa soña que levaban á gilotina. Levaban nun carro e a xente insultáballe. Chegou ao verdugo e colocáronlle a cabeza baixo o coitelo. Cando Aifría caía sobre o seu pescozo, deuse conta de que a súa muller estaba durmida e golpeouse un pequeno golpe de abanico no pescozo. A emoción provocou a morte do pobre Peter. Cal é a razón lóxica paira cuestionar este episodio?
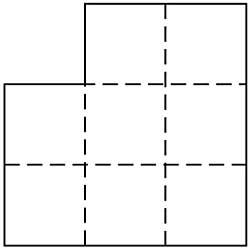
12. Debes dividir a imaxe en tres partes, recolléndoa adecuadamente paira obter un cadrado concreto. (Figura 5)
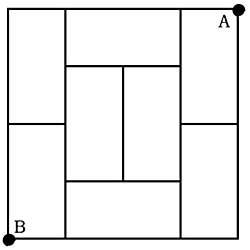
13. Una habitación está chea de oito tatamis, todos eles de 2x1 metros. Camiñando polos bordos dos tatamis, cal é o percorrido máis longo entre os puntos A e B? (non se pode pasar dúas veces polos bordos). (Figura 6)
14. Na figura 7 podes ver outro cubo dentro dun cubo. Estás seguro de que así é?
15. Imaxínache que conduces un autobús. Na primeira estación subiron 5 viaxeiros. Na seguinte subiron 5 e baixaron 7. O terceiro sobe 3 e non baixa ningún. Nos seguintes subíronse e baixado 8 e 5, 2 e 6, 7 e 4 respectivamente. Cantos anos ten o condutor?
16. As 15 bólas do billar americano colócanse formando un triángulo equilátero. Mirando por un vértice, poderías colocar cada bóla de forma que teña a diferenza das súas dúas bólas tangentes de atrás?
17. Tes que dividir un cadrado de 5x5 en catro partes, de forma que formen cadrados de 4x4 e 3x3. (Figura 8)
18. Se un reloxo de carillón tarda 2 segundos en tocar as dúas horas, canto tardará en soar as tres?
19. A letra M córtase con tres rectas paira obter nove triángulos. (Figura 9)

20. Que non! Non debuxar un cadrado con dúas rectas!
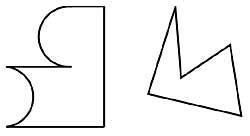
21. Dividir as dúas figuras laterais formando dúas pezas iguais en cada una delas. (Figura 10)
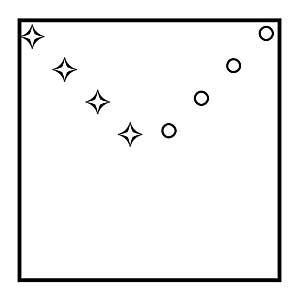
22. Como dividir o cadrado da figura 11 en catro partes do mesmo tamaño e aspecto, cada una cunha estrela e un círculo?
23. Nun grupo una persoa di: “o meu irmán morreu fai 130 anos”. Pode ser certo?
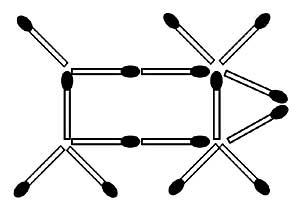
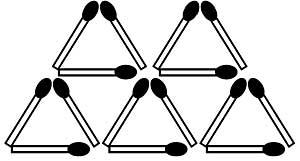
24. Ao mover dous poxpolos pódese conseguir que as vacas miren cara atrás. (Permítese que a cola quede arriba ou abaixo) (Figura 12)
25. Entre dúas moedas de cinco duros e pegadas colócase una dura. Hai que quitar o duro sen moverse polo centro.
26. Bota dez moedas a tres bosques deixando en cada un un número impar de moedas.
27. Agora dous exercicios máis sobre imaxes máxicas:
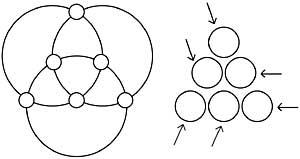
Escriba os números 1, 2, 3, 4, 5, 6 en círculos brancos para que as sumas dos números da mesma circunferencia sexan iguais.
Escribe agora os números 1, 2, 3, 4, 5, 6 para que a suma dos números das liñas que nos marcan as frechas sexan diferentes e sucesivos valores. (Figura 13)
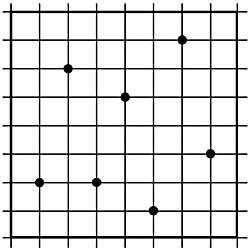
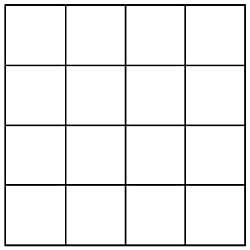
28. Agrupe correctamente os sete puntos marcados na táboa da figura 14, rodeando a menor superficie posible. Non se poden cortar entre si.
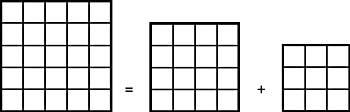
29. Copie a imaxe seguinte nun papel e recorte pola liña en po. Une as dúas pezas obtidas como se pode apreciar na figura 2. Os rectángulos das figuras 1 e 2 teñen a mesma lonxitude. Por tanto, teñen a mesma superficie. Con todo, o segundo rectángulo ten una superficie menor, ao faltarlle o cadrado central. Cal é a explicación deste paradoxo? (Figura 15)
30. Déronse conta de que as mulleres dun pobo son enganadas polos seus veciños, polo menos uno, e trasladaron a súa queixa aos seus representantes.
Os representantes, una vez localizados os veciños desleais, deciden enviar una carta ás mulleres. Nela aparecen os nomes dos veciños desleais, excepto a da muller á que se envía a carta, que pode enganar, pero quizais non. Os representantes autorizaron ás mulleres a castigar publicamente aos desleais veciños descubertos. Paira acertar a verdade, as mulleres cumprirán dúas condicións: una é non falar entre elas e outra é que só poidan ver si hai algún veciño desleal castigado ou non pola noite.
Pasado o primeiro día non houbo ningún castigo, nin despois do segundo. Así até a noite dos cuarentamarga, na que todos os veciños desleais foron castigados. Cantos veciños enganaron ás mulleres?
31. Un adulto e una nena deben cruzar o río; uno de esquerda a dereita, o outro ao revés. En cada beira hai una táboa, pero ambas algo máis curtas que a anchura do río. Que poden facer o adulto e a nena paira cruzar o río?
32. Escribe 64 utilizando só dous catro. Podes utilizar os símbolos matemáticos que queiras, pero en ningún caso máis números.
33. Movendo só dous poxpolos podes substituír os sete triángulos equiláteros da figura 16 por cinco. Conseguiralo?
34. No seu libro “Logika jokoa”, Lewis Carroll escribiu as seguintes frases:
- Ningunha oca baila
- Ningún militar pode deixar de bailar o vals cada vez que pode
- Todas as aves da miña barreira son gansos
Que conclusións lóxicas podes extraer destas tres frases?
35. Cales son os criterios das seguintes series numéricas? :
a) 1, 3, 5, 15, 30, 40, 50, ... b) 6, 8, 62, 63, 66, 72, 73, 76, 81, 84, ... c) 1, 101, 31, 131, 131, 1131,
2131 d) 1, 9, 2, 2, 5, 3, 4, 7, 8) 6, 2, 5, 5, 5, 4, 6, 6, 7, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 6, 6, 6, 6, 6, 7, 6, 6, 6, 6, 6, 6, 6, 2, 6, 6, 6, 3, 6, 6, 2, 3, 6, 3, 3, 3, 3, 3, 3,
3, 3, 7, 3, 7, 6, 6, 6, 3, 3, 6
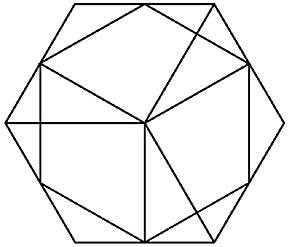
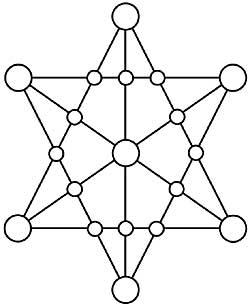
36. Localice os números 1 ao 19 nos círculos de hexagrama da figura 17 para que as sumas dos cinco números de cada liña sexan iguais.
37º Poderías completar 9 liñas de 5 moedas se só tes 21 moedas?
38º Pódese facer a seguinte imaxe sen levantar o bolígrafo do papel e pasar dúas veces por encima dunha raia? (Figura 18)
39. Un sabio quere medir o tempo de caída dun obxecto liberándoo dun ascensor que sobe. No 5º piso, e despois de deixar caer, o pequeno obxecto verde queda a dous pasos do investigador flotando no aire. Que motivos atopou o sabio paira explicar este incrible suceso?
40. Como situarías 5 moedas?
41. Despois de cinco puntos, como asociarías cada punto con outros dous puntos mediante correctores? De que formas pódese facer?
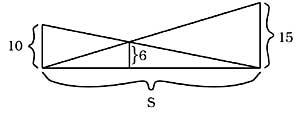
42. Cal é a lonxitude de S sen cálculo? (Figura 19)
43. Una paira responder moi rápido. Un pastor ten 17 ovellas. Se todos márchanse menos de nove, cantos quedaron?
44º Estaredes de acordo se una frase é falsa dicindo que é verdade a súa contraria, non? Por exemplo, “Esta frase ten seis palabras”, evidentemente é mentira. O contrario será “Esta frase non ten seis palabras”, pero tamén é mentira. Que opinas?
45. Multiplicando un número de dúas cifras polo dobre de 2 obtemos 3. Cal é o número?
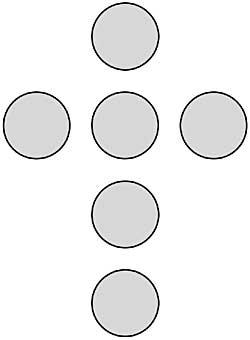
46. A continuación móstrase outro tipo de división. Debes dividir a lúa en seis partes por dúas rectas. Cadrada en oito triángulos agudos. E finalmente, a cruz con dúas liñas rectas, una pasando pola e a outra por B, paira poder formar un cadrado coas pezas que quedan. (Figura 20)

47. Nunha habitación hai tres sabios e cinco chapeus (tres brancos e dous negros). Por un momento apágase a luz e colócase un chapeu branco nas cabezas dos eruditos, os dous chapeus negros saíron sen ser vistos polos sabios. Enseguida acendeuse a luz. Cada sabio pode ver os chapeus dos demais, pero non o seu. Pregúntanlles a cor do chapeu que levan. Por un momento míranse e por último un di: o meu é branco. Por que acertou?
48º. Nunha nación de dez países, cada ano os recadadores de cada país debían dar 10 onzas de ouro ao Estado. Un ano un recadador quixo gardar un pouco de ouro. Paira iso ordenou eliminar un gramo de cada curtiduría, conservando o aspecto da vaina. Pero un xuíz foi avisado con toda precisión paira ter coidado coa recadación daquel ano, porque un recadador quería enganar.
O xuíz ordenou que todos os recadadores levasen todos os abonos á mesma hora do mesmo día. Pediu una balanza que pesaba gramos por gramo e despois de facer una pesada ante todos, puxo en evidencia ao estafador. Como o soubo?
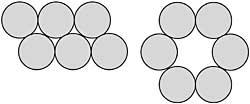
49º As moedas da esquerda da figura 21 deben situarse en tres movementos como na imaxe da dereita, respectando dúas regras
a)
en cada movemento móvese una moeda sen cambiar as outras,
b)
as moedas sempre deben tocar outras dúas moedas.
50. Cun movemento tes que formar dúas liñas de catro moedas. (Figura 22)
Tes un mes paira responder a estas preguntas. Esperámosche en setembro. Se non podes resolver algunha, cóntanos a túa solución. Temos todos. Non publicamos as preguntas nin as respostas no mesmo número porque non nos parece conveniente. Con todo, estamos dispostos a dar todas as explicacións na propia revista ou doutra maneira.





