Mezclado (II)
Con motivo de las vacaciones hemos querido traer a este número un nuevo revuelto. A la espera de que estos días tengas tiempo, hemos preparado 50 cuestionarios para que puedas llenar esta beta. Como en la anterior, aquí también puedes encontrar de todo: la luna, la vaca, los poxpolos, los cuadrados, las divisiones, los sueños, las gansos, los ojos, los rectos, ........................................................................................................................................................................................................... En general, si no son de broma, no te fíes, te puedes marear.
1. Si la persona fuera invisible, ¿lo vería?
El ojo que te traes no es
porque lo ves tú, es
porque te ve el ojo.
(Antonio Machado)
2. Una persona ve el oso y se desplaza hacia el sur corriendo 10 km. Desde allí ha recorrido otros 10 km al este y, finalmente, otros 10 km al norte. Mira dónde y el mismo oso vuelve a verlo. ¿De qué color es el oso?
3. Tenemos ocho monedas aparentemente iguales, pero una tiene menos peso que otras. ¿Se puede saber cuál es la moneda haciendo solo dos pesos?
4º ¿Qué signo hay que poner en el recuadro vacío? (Figura 1)

5. Se producía en un pueblo situado en la frontera entre los estados de Ibaibusti y Mendiberdea. Una libra de Ibaibusti costaba 90 céntimos de una libra de Mendiberdea. Asimismo, una libra de Mendiberde a 90 céntimos de una libra de Ibaibusti. Un día, una persona entró en un bar de la zona de Ibaibusti y pidió un zumo de 10 céntimos pagó con una libra local. A su regreso, en lugar de donar 90 céntimos de Ibaibusti, le dieron una libra de Mendiber-d. Más tarde se trasladó a un bar de Mendiberde y cuando pidió un mimbre de 10 céntimos pagó con la libera anterior, devolviendo 90 céntimos a una libera de Ibaibusti. De esta forma se desplazó una y otra vez de un bar a otro. Por último, tras beber todo lo que se quería, volvió a casa con el dinero que tenía al principio. ¿Quién pagó los mimbres?
6º Pon en tres pilas 11, 7 y 6 monedas. En tres movimientos debes dejar ocho monedas en tres montones. En los movimientos, a cada pila se le puede añadir tantas monedas como tenga y estas monedas deben proceder del mismo montón.
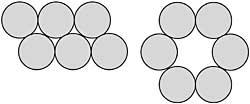
7. Tenemos dos cajas cúbicas iguales. En uno de ellos hay una bola de hierro de diámetro igual a la altura de la caja; en el otro, como se ve en la imagen, hay las mismas bolas de hierro. ¿Qué caja tiene más peso? (Figura 2)
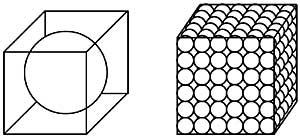
8º. La estrella de la figura 3 es mágica, ya que la suma de los cuatro números de sus seis líneas son 26. Sin embargo, la suma de los números de sus vértices es de 30. ¿Podría solucionarlo para conseguir una superestrella mágica, es decir, que la suma de los vértices también sea 26?
9. ¿Cómo se puede solucionar el siguiente producto que está mal sin añadir, quitar o escribir nada?
81. 9 = 801
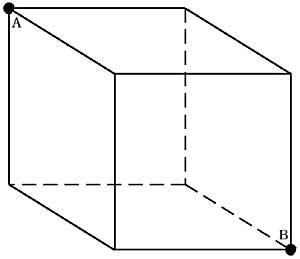
10. ¿Cuál es la ruta más corta para pasar de A a B por encima de la superficie del cubo? (Figura 4)
11. Este suceso tuvo lugar en un pueblo inglés, en la mañana y en la iglesia de un domingo. El sacerdote trabajaba en su sermón, como siempre. El sol quemaba. Debido al silencio que había en su interior y al rumor lejano de la calle, Peter se dormió. En tiempos de la revolución francesa sueña que llevaban a la gilotina. Llevaban en un carro y la gente le insultaba. Llegó al verdugo y le colocaron la cabeza bajo el cuchillo. Cuando Aifría caía sobre su cuello, se dio cuenta de que su mujer estaba dormida y se golpeó un pequeño golpe de abanico en el cuello. La emoción provocó la muerte del pobre Peter. ¿Cuál es la razón lógica para cuestionar este episodio?
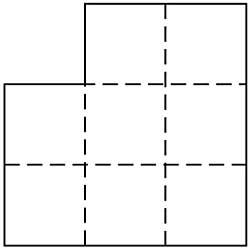
12. Debes dividir la imagen en tres partes, recogiéndola adecuadamente para obtener un cuadrado concreto. (Figura 5)
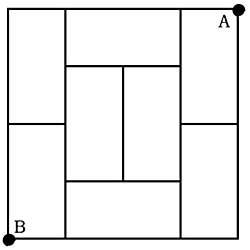
13. Una habitación está llena de ocho tatamis, todos ellos de 2x1 metros. Caminando por los bordes de los tatamis, ¿cuál es el recorrido más largo entre los puntos A y B? (no se puede pasar dos veces por los bordes). (Figura 6)
14. En la figura 7 puedes ver otro cubo dentro de un cubo. ¿Estás seguro de que así es?
15. Imagínate que conduces un autobús. En la primera estación han subido 5 viajeros. En la siguiente han subido 5 y han bajado 7. El tercero sube 3 y no baja ninguno. En los siguientes se han subido y bajado 8 y 5, 2 y 6, 7 y 4 respectivamente. ¿Cuántos años tiene el conductor?
16. Las 15 bolas del billar americano se colocan formando un triángulo equilátero. Mirando por un vértice, ¿podrías colocar cada bola de forma que tenga la diferencia de sus dos bolas tangentes de atrás?
17. Tienes que dividir un cuadrado de 5x5 en cuatro partes, de forma que formen cuadrados de 4x4 y 3x3. (Figura 8)
18. Si un reloj de carillón tarda 2 segundos en tocar las dos horas, ¿cuánto tardará en sonar las tres?
19. La letra M se corta con tres rectas para obtener nueve triángulos. (Figura 9)

20. ¡Que no! ¡No dibujar un cuadrado con dos rectas!
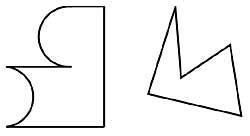
21. Dividir las dos figuras laterales formando dos piezas iguales en cada una de ellas. (Figura 10)
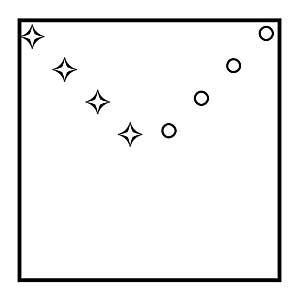
22. ¿Cómo dividir el cuadrado de la figura 11 en cuatro partes del mismo tamaño y aspecto, cada una con una estrella y un círculo?
23. En un grupo una persona dice: “mi hermano murió hace 130 años”. ¿Puede ser cierto?
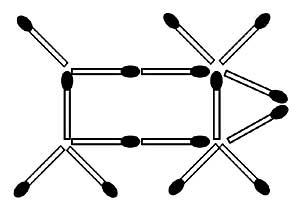
24. Al mover dos poxpolos se puede conseguir que las vacas miren hacia atrás. (Se permite que la cola quede arriba o abajo) (Figura 12)
25. Entre dos monedas de cinco duros y pegadas se coloca una dura. Hay que quitar el duro sin moverse por el centro.
26. Echa diez monedas a tres bosques dejando en cada uno un número impar de monedas.
27. Ahora dos ejercicios más sobre imágenes mágicas:
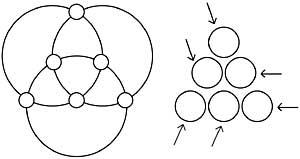
Escriba los números 1, 2, 3, 4, 5, 6 en círculos blancos para que las sumas de los números de la misma circunferencia sean iguales.
Escribe ahora los números 1, 2, 3, 4, 5, 6 para que la suma de los números de las líneas que nos marcan las flechas sean diferentes y sucesivos valores. (Figura 13)
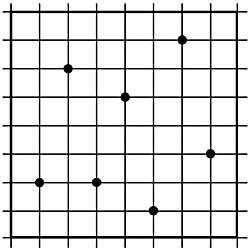
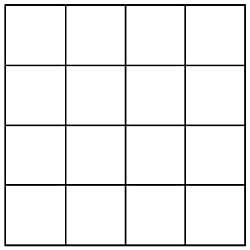
28. Agrupe correctamente los siete puntos marcados en la tabla de la figura 14, rodeando la menor superficie posible. No se pueden cortar entre sí.
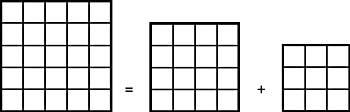
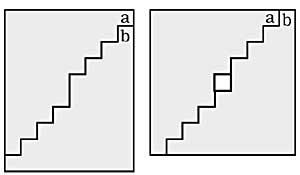
29. Copie la imagen siguiente en un papel y recorte por la línea en polvo. Une las dos piezas obtenidas como se puede apreciar en la figura 2. Los rectángulos de las figuras 1 y 2 tienen la misma longitud. Por lo tanto, tienen la misma superficie. Sin embargo, el segundo rectángulo tiene una superficie menor, al faltarle el cuadrado central. ¿Cuál es la explicación de esta paradoja? (Figura 15)
30. Se han dado cuenta de que las mujeres de un pueblo son engañadas por sus vecinos, al menos uno, y han trasladado su queja a sus representantes.
Los representantes, una vez localizados los vecinos desleales, deciden enviar una carta a las mujeres. En ella aparecen los nombres de los vecinos desleales, excepto la de la mujer a la que se envía la carta, que puede haber engañado, pero quizás no. Los representantes han autorizado a las mujeres a castigar públicamente a los desleales vecinos descubiertos. Para acertar la verdad, las mujeres cumplirán dos condiciones: una es no hablar entre ellas y otra es que sólo puedan ver si hay algún vecino desleal castigado o no por la noche.
Pasado el primer día no ha habido ningún castigo, ni después del segundo. Así hasta la noche de los cuarentamarga, en la que todos los vecinos desleales han sido castigados. ¿Cuántos vecinos han engañado a las mujeres?
31. Un adulto y una niña deben cruzar el río; uno de izquierda a derecha, el otro al revés. En cada orilla hay una tabla, pero ambas algo más cortas que la anchura del río. ¿Qué pueden hacer el adulto y la niña para cruzar el río?
32. Escribe 64 utilizando sólo dos cuatro. Puedes utilizar los símbolos matemáticos que quieras, pero en ningún caso más números.
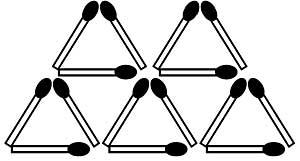
33. Moviendo sólo dos poxpolos puedes sustituir los siete triángulos equiláteros de la figura 16 por cinco. ¿Lo conseguirás?
34. En su libro “Logika jokoa”, Lewis Carroll escribió las siguientes frases:
- Ninguna oca baila
- Ningún militar puede dejar de bailar el vals cada vez que puede
- Todas las aves de mi barrera son gansos
¿Qué conclusiones lógicas puedes extraer de estas tres frases?
35. ¿Cuáles son los criterios de las siguientes series numéricas? :
a) 1, 3, 5, 15, 30, 40, 50, ... b) 6, 8, 62, 63, 66, 72, 73, 76, 81, 84, ... c) 1, 101, 31, 131, 131, 1131,
2131 d) 1, 9, 2, 2, 5, 3, 4, 7, 8) 6, 2, 5, 5, 5, 4, 6, 6, 7, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 6, 6, 6, 6, 6, 7, 6, 6, 6, 6, 6, 6, 6, 2, 6, 6, 6, 3, 6, 6, 2, 3, 6, 3, 3, 3, 3, 3, 3,
3, 3, 7, 3, 7, 6, 6, 6, 3, 3, 6
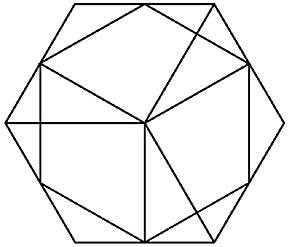
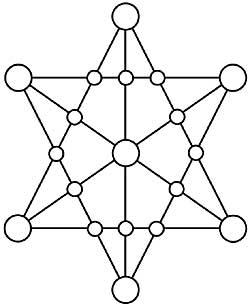
36. Localice los números 1 al 19 en los círculos de hexagrama de la figura 17 para que las sumas de los cinco números de cada línea sean iguales.
37º ¿Podrías completar 9 líneas de 5 monedas si solo tienes 21 monedas?
38º ¿Se puede hacer la siguiente imagen sin levantar el bolígrafo del papel y pasar dos veces por encima de una raya? (Figura 18)
39. Un sabio quiere medir el tiempo de caída de un objeto liberándolo de un ascensor que sube. En el 5º piso, y después de dejar caer, el pequeño objeto verde queda a dos pasos del investigador flotando en el aire. ¿Qué motivos encontró el sabio para explicar este increíble suceso?
40. ¿Cómo situarías 5 monedas?
41. Después de cinco puntos, ¿cómo asociarías cada punto con otros dos puntos mediante correctores? ¿De qué formas se puede hacer?
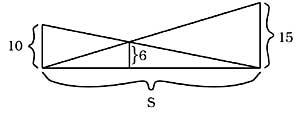
42. ¿Cuál es la longitud de S sin cálculo? (Figura 19)
43. Una para responder muy rápido. Un pastor tiene 17 ovejas. Si todos se marchan menos de nueve, ¿cuántos han quedado?
44º Estaréis de acuerdo si una frase es falsa diciendo que es verdad su contraria, ¿no? Por ejemplo, “Esta frase tiene seis palabras”, evidentemente es mentira. Lo contrario será “Esta frase no tiene seis palabras”, pero también es mentira. ¿Qué opinas?
45. Multiplicando un número de dos cifras por el doble de 2 obtenemos 3. ¿Cuál es el número?
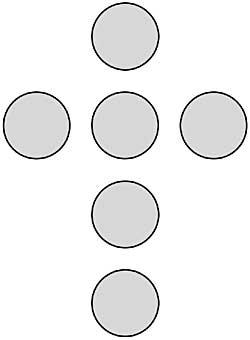
46. A continuación se muestra otro tipo de división. Debes dividir la luna en seis partes por dos rectas. Cuadrada en ocho triángulos agudos. Y finalmente, la cruz con dos líneas rectas, una pasando por A y la otra por B, para poder formar un cuadrado con las piezas que quedan. (Figura 20)

47. En una habitación hay tres sabios y cinco sombreros (tres blancos y dos negros). Por un momento se apaga la luz y se coloca un sombrero blanco en las cabezas de los eruditos, los dos sombreros negros han salido sin ser vistos por los sabios. Enseguida se ha encendido la luz. Cada sabio puede ver los sombreros de los demás, pero no el suyo. Les preguntan el color del sombrero que llevan. Por un momento se miran y por último uno dice: el mío es blanco. ¿Por qué ha acertado?
48º. En una nación de diez países, cada año los recaudadores de cada país debían dar 10 onzas de oro al Estado. Un año un recaudador quiso guardar un poco de oro. Para ello ordenó eliminar un gramo de cada curtiduría, conservando el aspecto de la vaina. Pero un juez fue avisado con toda precisión para tener cuidado con la recaudación de aquel año, porque un recaudador quería engañar.
El juez ordenó que todos los recaudadores se llevaran todos los abonos a la misma hora del mismo día. Pidió una balanza que pesaba gramos por gramo y después de hacer una pesada ante todos, puso en evidencia al estafador. ¿Cómo lo supo?
49º Las monedas de la izquierda de la figura 21 deben situarse en tres movimientos como en la imagen de la derecha, respetando dos reglas
a)
en cada movimiento se mueve una moneda sin cambiar las otras,
b)
las monedas siempre deben tocar otras dos monedas.
50. Con un movimiento tienes que formar dos líneas de cuatro monedas. (Figura 22)
Tienes un mes para responder a estas preguntas. Te esperamos en septiembre. Si no puedes resolver alguna, cuéntanos tu solución. Tenemos todos. No hemos publicado las preguntas ni las respuestas en el mismo número porque no nos parece conveniente. Sin embargo, estamos dispuestos a dar todas las explicaciones en la propia revista o de otra manera.





