Mixed (II)
On the occasion of the holidays we wanted to bring to this issue a new scramble. Waiting for you to have time these days, we have prepared 50 questionnaires so you can fill this beta. ..........................................................................................
1. If the person were invisible, would he see it?
The eye you bring is not because
you see it, it is
because you see the eye.
(Antonio Machado)
2. A person sees the bear and moves south running 10 km. From there he has traveled another 10 km east and finally another 10 km north. Look where and the same bear sees him again. What color is the bear?
3. We have eight seemingly equal coins, but one has less weight than others. Can you know what the currency is by making only two pesos?
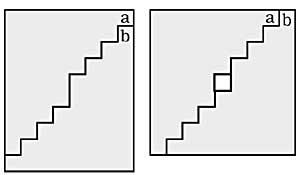
4º What sign must be put in the empty box? (Figure 1)

5. It was produced in a village located on the border between the states of Ibaibusti and Mendiberdea. A pound of Ibaibusti cost 90 cents of a pound of Mendiberdea. Likewise, a pound of Mendiberde at 90 cents of a pound of Ibaibusti. One day, a person entered a bar in the area of Ibaibusti and asked for a juice of 10 cents paid with a local pound. On his return, instead of donating 90 cents of Ibaibusti, he was given a pound of Mendiber-d. Later he moved to a bar in Mendiberde and when he asked for a wicker of 10 cents he paid with the previous release, returning 90 cents to a free one from Ibaibusti. In this way he moved again and again from one bar to another. Finally, after drinking everything he wanted, he returned home with the money he had at first. Who paid for the summits?
6º Put in three stacks 11, 7 and 6 coins. In three moves you must leave eight coins in three stacks. In movements, each stack can be added as many coins as it has and these coins must come from the same pile.
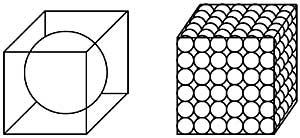
7. We have two equal cubic boxes. In one of them there is an iron ball of diameter equal to the height of the box; in the other, as seen in the image, there are the same iron balls. Which box has the most weight? (Figure 2)
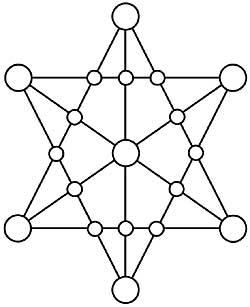
8th. The star of Figure 3 is magical, as the sum of the four numbers of its six lines is 26. However, the sum of the numbers of its vertices is 30. Could you solve it to get a magic superstar, that is, that the sum of the vertices is also 26?
9. How can you fix the next product that is wrong without adding, removing or writing anything?
81. 9 = 801
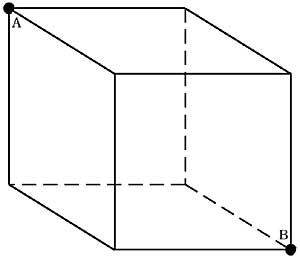
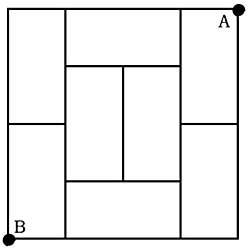
10. What is the shortest route to pass from A to B above the surface of the cube? (Figure 4)
11. This event took place in an English village, in the morning and in the church on a Sunday. The priest worked in his sermon, as always. The sun burned. Due to the silence inside and the distant rumor of the street, Peter fell asleep. At the time of the French revolution they dreamed that they were carrying gilotina. They were in a car and people insulted him. He came to the executioner and placed his head under the knife. When Aifrah fell on her neck, she realized that her wife was asleep and a small fan stroke hit her neck. The emotion caused the death of poor Peter. What is the logical reason to question this episode?
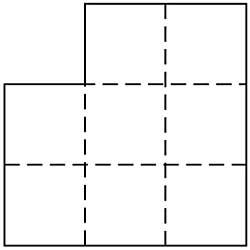
12. You must divide the image into three parts, collecting it properly to get a specific square. (Figure 5)
13. One room is full of eight tatamis, all of them 2x1 meters. Walking along the edges of the tatamis, what is the longest route between points A and B? (can not be passed twice on edges). (Figure 6)
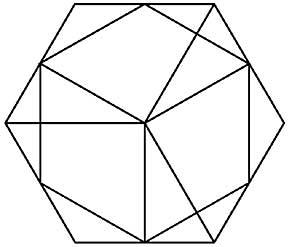
14. Figure 7 shows another cube inside a cube. Are you sure it is?
15. Imagine driving a bus. In the first station have gone up 5 travelers. In the next they have climbed 5 and have dropped 7. The third goes up 3 and none goes down. In the following have been uploaded and lowered 8 and 5, 2 and 6, 7 and 4 respectively. How old is the driver?
16. The 15 balls of the American billiards are placed forming an equilateral triangle. Looking at a vertex, could you place each ball so that it has the difference from its two tangent balls back?
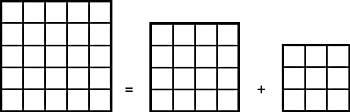
17. You have to divide a 5x5 square into four parts, so that they form 4x4 and 3x3 squares. (Figure 8)
18. If a carillon clock takes 2 seconds to play the two hours, how long will it take to ring the three?
19. The letter M is cut with three straight lines to obtain nine triangles. (Figure 9)

20. No! Do not draw a square with two straight lines!
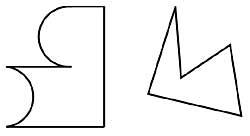
21. Divide the two side figures into two equal pieces in each of them. (Figure 10)
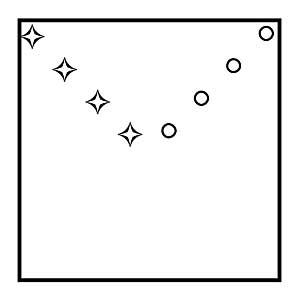
22. How to divide the square of figure 11 into four parts of the same size and appearance, each with a star and a circle?
23. In a group a person says: “My brother died 130 years ago.” Can it be true?
24. Moving two poxpoles allows cows to look back. (The tail is allowed up or down) (Figure 12)
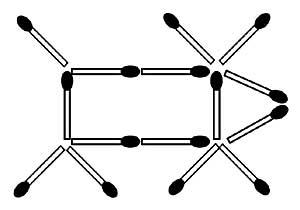
25. Between two coins of five hard and glued is placed a hard. You have to remove the hard without moving around the center.
26. Throw ten coins into three forests leaving each an odd number of coins.
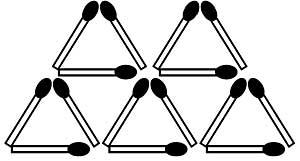
27. Now two more exercises on magical images:
Write the numbers 1, 2, 3, 4, 5, 6 in white circles so that the numbers in the same circle are equal.
Write now the numbers 1, 2, 3, 4, 5, 6 so that the sum of the numbers of the lines that mark the arrows are different and successive values. (Figure 13)
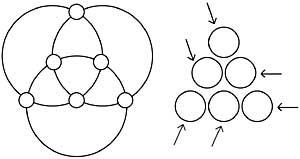
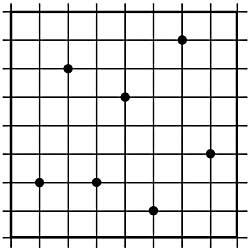
28. Group correctly the seven points marked in the table in Figure 14, surrounding the smallest possible surface. They cannot be cut together.
29. Copy the image below into a paper and crop the powder line. It joins the two pieces obtained as can be seen in Figure 2. The rectangles in figures 1 and 2 have the same length. Therefore, they have the same surface. However, the second rectangle has a smaller surface, as the central square is missing. What is the explanation of this paradox? (Figure 15)
30. They have realized that women in a village are deceived by their neighbors, at least one, and have moved their complaint to their representatives.
The representatives, once located the unloyal neighbors, decide to send a letter to the women. In it appear the names of the unloyal neighbors, except that of the woman to whom the letter is sent, who may have deceived, but perhaps not. The representatives have authorized women to publicly punish unloyal neighbors. To make the truth right, women will meet two conditions: one is not to speak between them and another is that they can only see if there is a disloyal neighbor punished or not at night.
After the first day there has been no punishment, nor after the second. So until the night of the quarantine, in which all unloyal neighbors have been punished. How many neighbors have deceived women?
31. An adult and a girl must cross the river; one from left to right, the other from the reverse. On each bank there is a board, but both somewhat shorter than the width of the river. What can the adult and girl do to cross the river?
32. Write 64 using only two four. You can use the mathematical symbols you want, but in no case more numbers.
33. Moving only two poxpoles you can replace the seven equilateral triangles of Figure 16 by five. Will you get it?
34. In his book “Logika jokoa”, Lewis Carroll wrote the following phrases:
- No goose dances
- No military can stop dancing the waltz every time they can
- All the birds of my barrier are geese
What logical conclusions can you draw from these three sentences?
35. What are the criteria for the following numerical series? :
6,
6, 3, 3, 3,
3
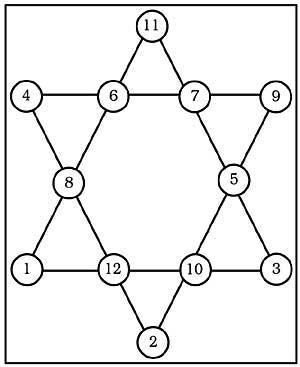
36. Locate numbers 1 to 19 in the hexagram circles of Figure 17 so that the sums of the five numbers of each line are equal.
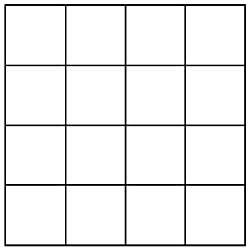
37º Could you complete 9 lines of 5 coins if you only have 21 coins?
38º Can the next image be made without lifting the pen from the paper and passing twice over a strip? (Figure 18)
39. A wise man wants to measure the falling time of an object by releasing it from a climbing elevator. On the 5th floor, and after dropping, the small green object is two steps from the researcher floating in the air. What reasons did the sage find to explain this incredible event?
40. How would you place 5 coins?
41. After five points, how would you associate each point with two other points by correctors? In what ways can it be done?
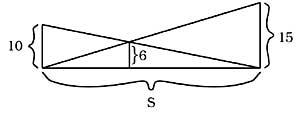
42. What is the length of S without calculation? (Figure 19)
43. One to respond very quickly. A shepherd has 17 sheep. If everyone leaves less than nine, how many are left?
44º You will agree if a phrase is false saying that it is true its opposite, right? For example, “This phrase has six words” is obviously a lie. The opposite will be “This phrase has no six words,” but it is also a lie. What do you think?
45. Multiplying a number of two figures by double 2 we get 3. What is the number?
46. Below is another type of division. You must divide the moon into six parts by two straight. Square in eight sharp triangles. And finally, the cross with two straight lines, one passing through A and the other through B, in order to form a square with the remaining pieces. (Figure 20)

47. In one room there are three wise men and five hats (three white and two black). For a moment the light is extinguished and a white hat is placed on the heads of the scholars, the two black hats have come out without being seen by the wise. Soon the light was lit. Every sage can see the hats of others, but not his. They ask them the color of the hat they wear. For a moment they look and finally one says: mine is white. Why did he succeed?
48º. In a nation of ten countries, each year the collectors of each country had to give 10 ounces of gold to the state. One year a collector wanted to keep some gold. To do this he ordered to remove a gram of each tannery, preserving the appearance of the sheath. But a judge was precisely warned to be careful about the collection that year, because a collector wanted to cheat.
The judge ordered that all the collectors take all the subscriptions at the same time of the same day. He asked for a balance that weighed grams per gram and after making a heavy before everyone, he exposed the scammer. How did you know?
49º The coins on the left of figure 21 must be placed in three movements as in the image on the right, respecting two rules
a)
in each movement moves one currency without changing the others,
b)
coins should always touch other two coins.
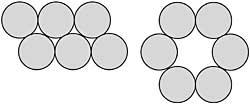
50. With a move you have to form two lines of four coins. (Figure 22)
You have a month to answer these questions. We wait for you in September. If you can't solve any, tell us your solution. We have all. We have not published the questions or answers in the same number because it does not seem convenient to us. However, we are willing to give all the explanations in the journal itself or otherwise.





