Mélange (II)
A l'occasion des vacances, nous avons voulu apporter à ce numéro un nouveau brouillé. En attendant que vous ayez le temps, nous avons préparé 50 questionnaires pour que vous puissiez remplir cette bêta. ............................................................................
1. Si la personne était invisible, le verrait-elle ?
L'oeil que vous portez n'est pas parce que
vous le voyez, c'est
parce que vous voyez l'oeil.
(Antonio Machado)
2. Une personne voit l'ours et se déplace vers le sud en courant 10 km. De là, il a parcouru encore 10 km à l'est et enfin 10 km au nord. Regardez où et le même ours le voit à nouveau. De quelle couleur est l'ours ?
3. Nous avons huit pièces apparemment égales, mais on a moins de poids que d'autres. Pouvez-vous savoir quelle est la monnaie ne faisant que deux poids?
4º Quel signe faut-il mettre dans la case vide? (Figure 1)

5. Elle se produisait dans un village situé à la frontière entre les états d'Ibaibusti et de Mendiberdea. Une livre d'Ibaibusti coûtait 90 cents d'une livre de Mendiberdea. De même, une livre de Mendiberde à 90 cents d'une livre d'Ibaibusti. Un jour, une personne est entrée dans un bar de la région d'Ibaibusti et a demandé un jus de 10 cents a payé avec une livre locale. À son retour, au lieu de donner 90 cents d'Ibaibusti, ils lui donnèrent une livre de Mendiber-d. Plus tard, il se rendit à un bar de Mendiberde et quand il demanda un osier de 10 cents il paya avec la libère précédente, en rendant 90 cents à une libère d'Ibaibusti. De cette façon, il s'est déplacé encore et encore d'un bar à l'autre. Enfin, après avoir bu tout ce qu'il voulait, il rentra chez lui avec l'argent qu'il avait au début. Qui a payé les mimbres ?
6ème Mettez en trois piles 11, 7 et 6 pièces. En trois mouvements, vous devez laisser huit pièces dans trois piles. Dans les mouvements, chaque pile peut être ajouté autant de pièces que vous avez et ces pièces doivent provenir de la même pile.
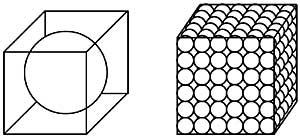
7. Nous avons deux boîtes cubiques identiques. Dans l'un d'eux il y a une boule de fer de diamètre égale à la hauteur de la boîte; dans l'autre, comme on le voit dans l'image, il y a les mêmes boules de fer. Quelle boîte a plus de poids? (Figure 2)
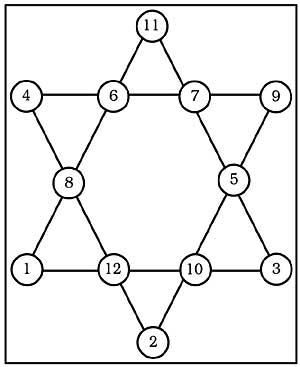
8º. L'étoile de la figure 3 est magique, puisque la somme des quatre nombres de ses six lignes sont 26. Cependant, la somme des nombres de leurs sommets est de 30. Pourriez-vous y remédier pour obtenir une superstar magique, c'est-à-dire que la somme des sommets soit aussi 26 ?
9. Comment pouvez-vous résoudre le produit suivant qui est mal sans ajouter, supprimer ou écrire quoi que ce soit?
81. 9 = 801
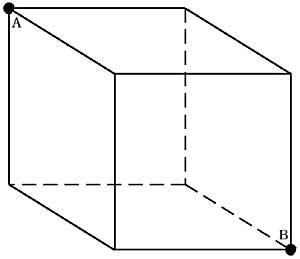
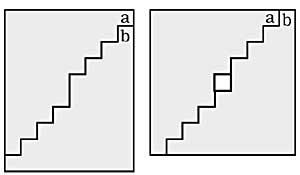
10. Quel est le chemin le plus court pour passer de A à B au-dessus de la surface du cube ? (Figure 4)
11. Cet événement a eu lieu dans un village anglais, le matin et dans l'église d'un dimanche. Le prêtre travaillait dans son sermon, comme toujours. Le soleil brûlait. En raison du silence qu'il y avait à l'intérieur et au bruit lointain de la rue, Peter s'est endormi. Au temps de la révolution française, il rêve qu'ils portaient la gilotine. Ils portaient sur un chariot et les gens l'insultaient. Il arriva au bourreau et on lui mit la tête sous le couteau. Quand Aifresco tombait sur son cou, elle a réalisé que sa femme était endormie et a frappé un petit coup d'éventail sur son cou. L'émotion a provoqué la mort du pauvre Peter. Quelle est la raison logique pour remettre en question cet épisode?
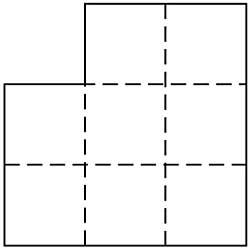
12. Vous devez diviser l'image en trois parties, la ramasser correctement pour obtenir un carré particulier. (Figure 5)
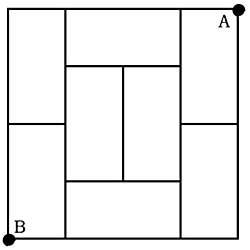
13. Une chambre est pleine de huit tatamis, tous de 2x1 mètres. En marchant sur les bords des tatamis, quel est le parcours le plus long entre les points A et B ? (on ne peut pas passer deux fois par les bords). (Figure 6)
14. Dans la figure 7, vous pouvez voir un autre cube dans un cube. Êtes-vous sûr que c'est le cas ?
15. Imaginez que vous conduisez un bus. Au premier poste, 5 voyageurs sont montés. Dans la suivante, ils ont augmenté 5 et ont baissé 7. Le troisième monte 3 et ne descend aucun. Les 8 et 5, 2 et 6, 7 et 4 ont été respectivement téléchargés et descendus. Combien d'années le conducteur a-t-il ?
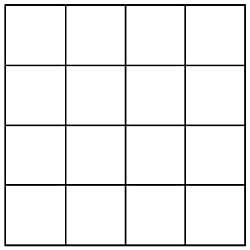
16. Les 15 billes de billard américain sont placées en formant un triangle équilatéral. En regardant par un sommet, pourriez-vous placer chaque boule de façon à avoir la différence de ses deux billes tangentes arrière ?
17. Vous devez diviser un carré de 5x5 en quatre parties, de sorte qu'ils forment des carrés de 4x4 et 3x3. (Figure 8)
18. Si une montre de carillon prend 2 secondes pour jouer les deux heures, combien de temps faut-il pour sonner les trois?
19. La lettre M est coupée en trois lignes droites pour obtenir neuf triangles. (Figure 9)

20. Non ! Ne pas dessiner un carré avec deux droites!
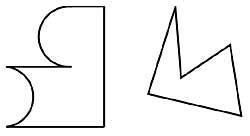
21. Diviser les deux figures latérales en deux pièces égales dans chacune d'elles. (Figure 10)
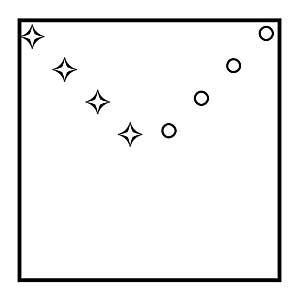
22. Comment diviser le carré de la figure 11 en quatre parties de la même taille et l'aspect, chacune avec une étoile et un cercle ?
23. Dans un groupe, une personne dit: « Mon frère est mort il y a 130 ans. » Est-ce possible ?
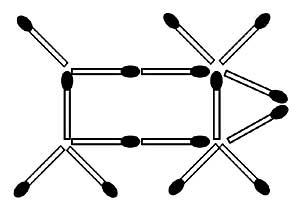
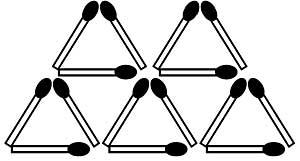
24. Lorsque vous déplacez deux poxpoles, vous pouvez obtenir que les vaches regardent en arrière. (La queue est autorisée en haut ou en bas) (Figure 12)
25. Entre deux pièces de cinq durs et collés est placé une dure. Il faut enlever le dur sans se déplacer dans le centre.
26. Jetez dix pièces dans trois bois, laissant dans chacun un nombre impair de pièces.
27. Maintenant deux autres exercices sur les images magiques:
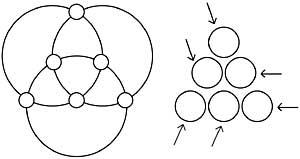
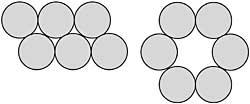
Écrivez les nombres 1, 2, 3, 4, 5, 6 en cercles blancs pour que les sommes des nombres de la même circonférence soient égales.
Ecris maintenant les nombres 1, 2, 3, 4, 5, 6 pour que la somme des nombres des lignes qui marquent les flèches soient différentes et successives valeurs. (Figure 13)
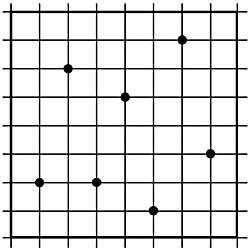
28. Regrouper correctement les sept points marqués sur le tableau de la figure 14, en entourant la plus petite surface possible. Ils ne peuvent pas être coupés entre eux.
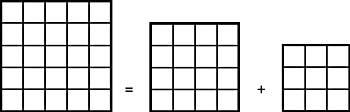
29. Copiez l'image suivante sur un papier et découpez la ligne en poudre. Joignez les deux pièces obtenues comme vous pouvez le voir dans la figure 2. Les rectangles des figures 1 et 2 ont la même longueur. Par conséquent, ils ont la même surface. Cependant, le deuxième rectangle a une surface inférieure, en manquant le carré central. Quelle est l'explication de ce paradoxe ? (Figure 15)
30. Ils ont réalisé que les femmes d'un village sont trompées par leurs voisins, au moins un, et ont transféré leur plainte à leurs représentants.
Les représentants, une fois les voisins déloyaux localisés, décident d'envoyer une lettre aux femmes. On y trouve les noms des voisins déloyaux, sauf celui de la femme à qui la lettre est envoyée, qui peut avoir trompé, mais peut-être pas. Les représentants ont autorisé les femmes à punir publiquement les voisins déloyaux découverts. Pour réussir la vérité, les femmes rempliront deux conditions: l'une est de ne pas parler entre elles et l'autre est qu'elles ne peuvent voir s'il y a un voisin déloyal puni ou pas la nuit.
Après le premier jour, il n'y a eu aucune punition, ni après le second. Ainsi jusqu'à la nuit des quarters, où tous les voisins déloyaux ont été punis. Combien de voisins ont trompé les femmes?
31. Un adulte et une fille doivent traverser la rivière; l'un de gauche à droite, l'autre à l'envers. Sur chaque bord il y a une table, mais les deux légèrement plus courtes que la largeur de la rivière. Que peuvent faire l'adulte et la fille pour traverser la rivière?
32. Ecrire 64 en utilisant seulement deux quatre. Vous pouvez utiliser les symboles mathématiques que vous voulez, mais en aucun cas plus de nombres.
33. En ne déplaçant que deux poxpoles, vous pouvez remplacer les sept triangles équilatéraux de la figure 16 par cinq. Allez-vous l'obtenir?
34. Dans son livre “Logika jokoa”, Lewis Carroll a écrit les phrases suivantes:
- Aucune oie ne danse
- Aucun militaire ne peut arrêter de danser la valse chaque fois qu'il peut
- Tous les oiseaux de ma barrière sont des oies
Quelles conclusions logiques pouvez-vous tirer de ces trois phrases?
35. Quels sont les critères des séries numériques suivantes ? :
3, 3, 5, 15, 30, 40, 50, ... b) 6, 8, 62, 63, 66, 72, 73, 76, 81, 84, ... c) 1, 101, 31, 131, 131, 1131,
2131 d) 1, 9, 2, 2, 5, 3, 4, 7, 8) 6, 2, 5, 5, 4, 6, 6, 6, 7, 3, 3, 3
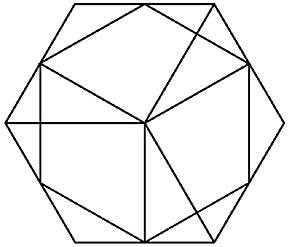
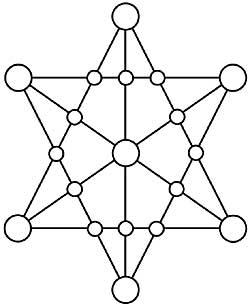
36. Localisez les nombres 1 à 19 dans les cercles d'hexagramme de la figure 17 pour que les sommes des cinq nombres de chaque ligne soient égales.
37º Pourriez-vous compléter 9 lignes de 5 pièces si vous n'avez que 21 pièces?
38º Pouvez-vous faire l'image suivante sans soulever le stylo du papier et passer deux fois au-dessus d'une ligne? (Figure 18)
39. Un sage veut mesurer le temps de chute d'un objet en le libérant d'un ascenseur qui monte. Au 5ème étage, et après la chute, le petit objet vert se trouve à deux pas du chercheur flottant dans l'air. Quels motifs le sage a-t-il trouvé pour expliquer cet événement incroyable ?
40. Comment situeriez-vous 5 pièces ?
41. Après cinq points, comment associeriez-vous chaque point à deux autres points avec des correcteurs ? De quelles façons pouvez-vous faire?
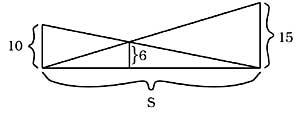
42. Quelle est la longueur de S sans calcul? (Figure 19)
43. Une réponse très rapide. Un berger a 17 brebis. Si tous partent moins de neuf, combien sont-ils restés ?
44º Vous serez d'accord si une phrase est fausse disant que c'est vrai son contraire, non? Par exemple, “Cette phrase a six mots”, c’est évidemment un mensonge. Le contraire sera “Cette phrase n'a pas six mots”, mais c'est aussi un mensonge. Que pensez-vous ?
45. En multipliant un nombre de deux chiffres pour le double de 2 nous obtenons 3. Quel est le nombre ?
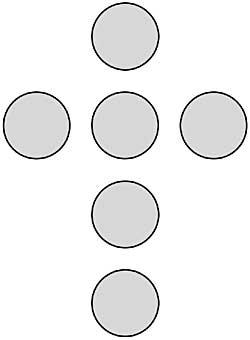
46. Voici un autre type de division. Vous devez diviser la lune en six parties par deux droites. Carrée en huit triangles aigus. Et enfin, la croix avec deux lignes droites, l'une passant par A et l'autre par B, pour pouvoir former un carré avec les pièces restantes. (Figure 20)

47. Dans une chambre il y a trois sages et cinq chapeaux (trois blancs et deux noirs). Pendant un moment la lumière s'éteint et un chapeau blanc est placé sur les têtes des savants, les deux chapeaux noirs sont sortis sans être vu par les sages. Tout de suite la lumière a été allumée. Chaque sage peut voir les chapeaux des autres, mais pas le sien. Ils leur demandent la couleur du chapeau qu'ils portent. Pour un moment, on regarde et enfin on dit: le mien est blanc. Pourquoi avez-vous réussi?
48°. Dans une nation de dix pays, chaque année les collecteurs de chaque pays devaient donner 10 onces d'or à l'État. Un an un collecteur a voulu garder un peu d'or. Pour ce faire, il a ordonné d'enlever un gramme de chaque tannerie, en conservant l'aspect de la gaine. Mais un juge a été avisé en toute précision de faire attention à la collecte de cette année, parce qu'un collecteur voulait tromper.
Le juge a ordonné que tous les collecteurs prennent tous les abonnements à la même heure le même jour. Il a demandé une balance pesant grammes par gramme et après avoir fait une lourde face à tous, il a mis en évidence le arnaque. Comment avez-vous su?
49º Les pièces de la gauche de la figure 21 doivent se situer en trois mouvements comme dans l’image de droite, en respectant deux règles
a) a)
dans chaque mouvement se déplace une pièce sans changer les autres,
b)
Les pièces doivent toujours toucher deux autres pièces.
50. Avec un mouvement, vous devez former deux lignes de quatre pièces. (Figure 22)
Vous avez un mois pour répondre à ces questions. Nous vous attendons en septembre. Si vous ne pouvez pas résoudre un problème, dites-nous votre solution. Nous avons tous. Nous n'avons pas publié les questions ni les réponses dans le même numéro parce qu'il ne nous semble pas approprié. Cependant, nous sommes prêts à donner toutes les explications dans le propre magazine ou autrement.





