Maurits Cornelis Escher (e III)
Mundos imposibles
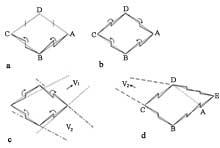
Tamén tratou o tema de mundos imposibles. Antes de mencionar algunhas imaxes, analicemos cun exemplo a esencia das mesmas (figura 1). Na imaxe pódese ver un rombo e un cadrado pegados e todas as imaxes son iguais excepto a sombra. As figuras superior e inferior poden entenderse de dúas formas, segundo indícase nelas. O mesmo ocorre con todo o que vemos. O que pasa é que moitos detalles que vemos sen darnos conta teñen una interpretación inconfundible. Sen eles o ángulo de incidencia da luz xera diferentes interpretacións.
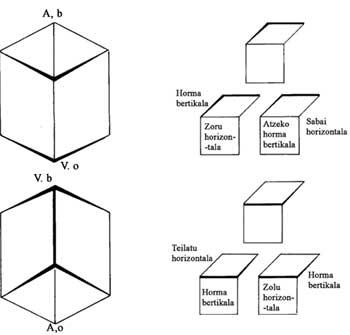

Na imaxe cóncava e convexa, os templos cúbicos ojivales forman o elemento arquitectónico máis importante [1]. Por iso representamos os cubos adxacentes con dúas interpretacións (figura 2). Axiña que como se ve apréciase a simetría da imaxe; o filtrado central non é brusco, senón graduado. Pero despois da metade, a parte superior vólvese baixa e a dianteira convértese en traseira. Os seres humanos, lagartijas e lorapotes, pola súa banda, enfróntanse ao investimento. Con todo, si quixesen cambiar de parte (de esquerda a dereita ou viceversa) pagarían caro. Por exemplo, si o que está a subir pola escaleira na parte inferior esquerda quixese dar a volta ao templo, pasar por diante da sentada, pasar a cuncha central e subir polas escaleiras que ten diante, asustaríase ao darse conta de que a escaleira que estaba aos seus pés converteuse nun teito. O mesmo pasaría a todos os personaxes que están á esquerda.

É sorprendente a bóveda situada entre os dous dulzaineros. Mentres que paira o da esquerda é o tellado, é dicir, el pode saltar, paira o da dereita o teito é o teito, é dicir, se saltase caería até o chan.

Na figura 2 dividiuse o cadro en catro partes. A parte esquerda ten una arquitectura convexa, coma se puidésemos ver todos os puntos desde arriba. Na parte dereita utilízase a arquitectura cóncava, é dicir, vémolo todo desde abaixo. Nas dúas partes centrais a interpretación é dobre, á marxe dos humanos, lagartijas e lorapotes.
Toda imaxe da realidade é una proxección sobre a superficie plana desa realidade. Calquera figura de superficie launa non ten por que ser a proxección da realidade tridimensional. É o caso de Belvedere, 1958, na litografía, que nos dá a solución o propio cadro [2]. A clave está nesa especie de cubo que ten o mozo que aparece sentado nel (figura 3). Vexamos os cubos adxacentes. Na primeira temos dúas opcións, dependendo de que os vértices 1 e 4 estean máis ou menos preto de nós que os vértices 2 e 3. Así mesmo, os vértices 2 e 4 poderían verse máis cerca que o resto, a pesar de contravenir a nosa idea de cubo na nosa mente. Se damos volume aos bordos do cubo, entre outras cousas, poderiamos conseguir “cubos” b e c, en contra do que os nosos sentidos teñen (figura 4).
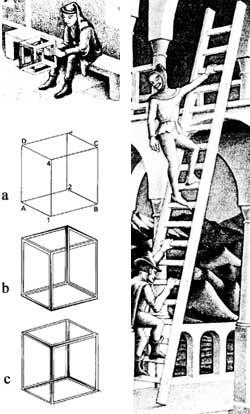

En Belvedere podemos ver á vez a escaleira interior e exterior. A dirección do eixo longitudinal do piso superior é a que ve a muller. A de abaixo, a do home, que forma un ángulo recto. As columnas que unen o primeiro e segundo piso, salvo as dos extremos, unen os lados anterior e posterior, é dicir, están en diagonal e non verticais. A imaxe pódese dividir horizontalmente en dúas, sendo as partes superior e inferior rectas (edificables). Con todo, ambas non poden existir simultaneamente.
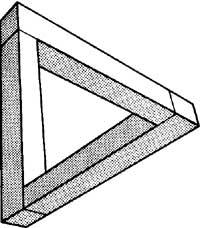
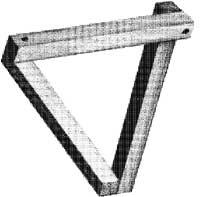
R. representadas nas figuras 5 e 6. A litografía Fervenza de Escher (1961) foi suxerida por “tribar” de Penrose. A tribarra, do mesmo xeito que os cubos anteriores, non se pode construír en tres dimensións. Si en “Salto de auga” fixámonos só na auga, empezando polo turtuco, ao longo da canle, a auga vaise afastando cara á dereita, logo cara á esquerda, cara á dereita de novo e por último cara á esquerda, paira saír ao turco. Este tribar e salto de auga producen o mesmo efecto (Figura 7).


Baseouse noutra imaxe de Penrose paira a litografía da Escaleira de Escher, arriba, abaixo, 1960 (Figura 8). Nesta imaxe quixo explicar a idea do infinito. Paira iso utilizouse a escaleira que sempre sobe (ou baixa) de Penros. Se seguimos aos personaxes que están no exterior, aínda que sempre subamos, despois de dar una volta completa darémonos conta de que se atopan no mesmo lugar. A trampa queda ao descuberto si cortamos o edificio en serras horizontais. A primeira capa atópase a un nivel inferior ao resto, é dicir, as capas non están superpuestas, senón que forman un espiral.
Na figura 9 pódese observar, en plano horizontal, como se pode obter una escaleira en continuo ascenso (9 a, c). Pero esta solución ten un problema. Pérdese perspectiva, xa que os puntos de escape, V1 e V2, quedan baixo o bautizo. Isto pode resolverse se se alarga a dúas caras (9 d). O debuxo de Escher indícanos que esta solución é válida.
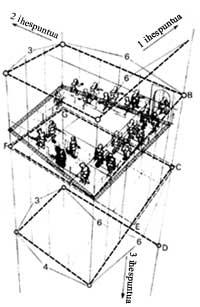
Sabemos como nos engana a imaxe: a escaleira atópase nun plano horizontal, mentres que o resto de detalles da imaxe (plintos de columnas, marcos de xanelas, etc.) adiántanse en forma de espiral. Se trazamos rectas verticais en cada nivel, observamos que estas liñas forman un prisma de proporcións 6:6:3:4. Todos os puntos da imaxe situados á mesma altura forman un espiral (liña de punto) (Figura 10).
Aproximación ao infinito
Nun artigo escrito en 1959, Escher afirmou literalmente o que motivaba a representar o infinito: “É imposible pensar que non hai nada máis aló das estrelas máis afastadas que vemos no horizonte. (…). Por iso, desde que o home está no chan (de pé, sentado ou tombado, corre, navega, vai dacabalo e voa), máis aló da presenza do purgatorio, o ceo e o inferno, mantemos a idea da transmigración e a miña, todos eles espazos de infinito ancho ou estados de infinita duración no tempo”.
Coa partición regular da superficie aínda non se conseguiu o infinito, senón só parte dela. Pero a habilidade de Escher na partición regular da superficie resultoulle moi útil. Con todo, necesitábase un elemento novo: una estrutura que permitise representar a superficie infinita nunha superficie finita.
En 1937 realiza a súa primeira sesión utilizando imaxes congruentes. En 1939 utilizou imaxes uniformes, pero a idea da metamorfose seguía predominando. Só desde 1955 utilizou imaxes uniformes paira formar series que suxiren infinito. Estes traballos pódense dividir en tres seccións, dependendo da estrutura que hai debaixo da imaxe: imaxes cadradas, imaxes espirales e as imaxes suxeridas por Coxeter.
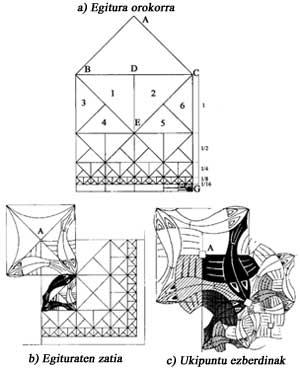
A figura 11 a mostra una solución ao problema de representación do infinito. Se a diferenza do cadrado EFCD é de 10 cm, a parte inferior será de 5 cm, e a seguinte de 2,5 cm, etc. CG 20 cm, pero podemos ver infinitos cadrados cada vez máis pequenos. Escher utilizou esta estrutura paira ilustrar un manual sobre a partición regular da superficie.

Limite cadrado, 1964, debuxo en madeira, cunha estrutura máis complexa [3], pero baseada na anterior (Figura 11 b). Paira comprender mellor a imaxe, una vez coñecida a infraestrutura, explicaremos por que aparecen tres cores. Observando os puntos nos que os peixes se tocan, observaremos que son de tres tipos (Figura 11 c). No punto A recóllense catro aletas de catro peixes, no punto B catro cabezas e catro colas, e no punto C tres aletas. Nos puntos A e B non se necesita máis de dúas cores. No punto C son necesarios tres cores. Os puntos A só están en diagonais. Por último, as cores que se recollen nos puntos A e B aparecen en diferentes combinacións.
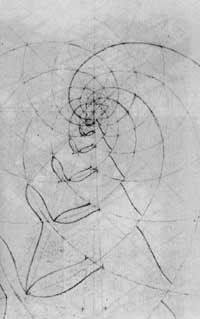
A estrutura que se atopa debaixo das figuras das espirales é una espiral logarítmica. Este concepto matemático non o coñecía Escher e descubriuno da seguinte maneira (Figura 12): representou as primeiras circunferencias concéntricas, diminuíndo as distancias entre elas cara ao centro. Logo trazou os radios que dividían as circunferencias nos mesmos arcos. Partindo dun punto da circunferencia exterior, marcou os puntos que cortan os radios e as circunferencias para que una vez unidos formasen a espiral.
A súa traxectoria vital I, 1958, empregou dobre espiral que partía de 8 puntos da circunferencia. En Traxectoria vital II, 1958, os puntos de partida son catro e en Traxectoria vital III, 1966, doce espirales parten de 6 puntos.

A traxectoria vital II mostra que dúas espirales que parten de dous puntos diferentes da circunferencia están unidas desde o exterior. Deste xeito, pódese chegar até o centro desde o límite exterior e de aí volver ao momento de partida (Figura 13). Na imaxe pódese ver o espiral vermella cara ao centro e o espiral azul que salgue do centro, coincidentes no seu parte exterior.
En Ubila, 1957, o debuxo era anterior ao ciclo de vida e non esgotara todas as posibilidades [4]. Nas zonas superior e inferior aparecen dous espirales que se desprazan na mesma dirección. As espirales debuxáronse por detrás de dous peixes en sentido contrario. Só se utilizaron dous ferros de impresión. Paira a representación dos peixes grises e vermellos superiores utilizáronse as dúas láminas de peces inferiores vermellos e grises.
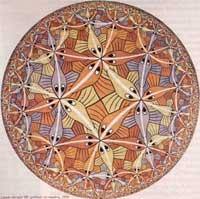
Paira representar a serie de limite circular, Escher H. Baseouse no modelo utilizado polo matemático Poincare paira representar a xeometría parabólica. Modelo HSM Atopouno nun libro de Coxeter (figura 14). Así naceu o Limite circular de 1958 I (pouco traballo). En Limite circular II, similar ao anterior, substituíu aos peixes por cruces. O limite circular IV, 1960, tamén se basea na imaxe de Coxeter. En cambio, Limite circular III, 1959 modificou a infraestrutura [5]. Segundo o propio Escher: “Os erros do primeiro elimináronse na medida do posible. Nesta ocasión, todos os peixes dunha serie teñen o mesmo cor e van tras o bautizo, que van crecendo a medida que se achegan ao centro. (…). Ningún compoñente afecta o límite ....


A serpe, 1969, debuxou en madeira antes de sufrir una complicada operación [6]. A pesar de ter 71 anos, a man non vibrou no seu último traballo. Na disputa por expresar o infinito apréciase una maior humildade (nas figuras anteriores, con axuda dunha lupa, debuxou figuras que medían menos de medio milímetro). A serpe non acabou coa serie de pequenos aneis.
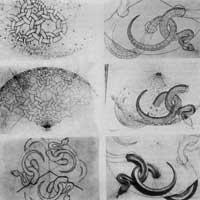
Cando suxeriu una diminución continua de tamaño abandonouno (Figura 15). Nos bosquexos percibimos a infraestrutura de Coxeter desde os grandes aneis cara a fóra. Pero consegue o mesmo efecto cara a dentro, creando una liña ondulada. As serpes, tras ver moitas fotos, representounas de memoria. Estudos previos pon de manifesto a pulcritude de Escher por cada detalle. Esa foi una das características de Escher.
Vimos a vida e o traballo de Escher. Utilizou moitas estruturas matemáticas sen sabelo. Por iso trouxemos a esta sección a este ilustrador. A pesar de que Escher morreu fai 20 anos, deixounos o seu traballo. Gózaos!






