Maurits Cornelis Escher (y III)
Mundos imposibles
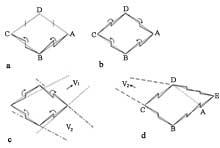
También trató el tema de mundos imposibles. Antes de mencionar algunas imágenes, analicemos con un ejemplo la esencia de las mismas (figura 1). En la imagen se puede ver un rombo y un cuadrado pegados y todas las imágenes son iguales excepto la sombra. Las figuras superior e inferior pueden entenderse de dos formas, según se indica en ellas. Lo mismo ocurre con todo lo que vemos. Lo que pasa es que muchos detalles que vemos sin darnos cuenta tienen una interpretación inconfundible. Sin ellos el ángulo de incidencia de la luz genera diferentes interpretaciones.
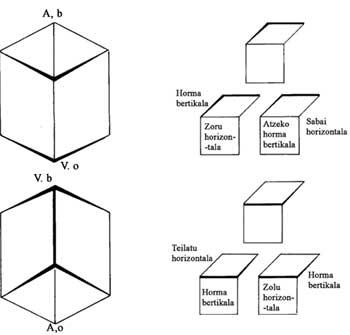

En la imagen cóncava y convexa, los templos cúbicos ojivales forman el elemento arquitectónico más importante [1]. Por eso hemos representado los cubos adyacentes con dos interpretaciones (figura 2). Tan pronto como se ve se aprecia la simetría de la imagen; el filtrado central no es brusco, sino escalonado. Pero después de la mitad, la parte superior se vuelve baja y la delantera se convierte en trasera. Los seres humanos, lagartijas y lorapotes, por su parte, se enfrentan a la inversión. Sin embargo, si quisieran cambiar de parte (de izquierda a derecha o viceversa) pagarían caro. Por ejemplo, si el que está subiendo por la escalera en la parte inferior izquierda quisiera dar la vuelta al templo, pasar por delante de la sentada, pasar la concha central y subir por las escaleras que tiene delante, se asustaría al darse cuenta de que la escalera que estaba a sus pies se ha convertido en un techo. Lo mismo pasaría a todos los personajes que están a la izquierda.

Es sorprendente la bóveda situada entre los dos dulzaineros. Mientras que para el de la izquierda es el tejado, es decir, él puede saltar, para el de la derecha el techo es el techo, es decir, si saltara caería hasta el suelo.

En la figura 2 se ha dividido el cuadro en cuatro partes. La parte izquierda tiene una arquitectura convexa, como si pudiéramos ver todos los puntos desde arriba. En la parte derecha se utiliza la arquitectura cóncava, es decir, lo vemos todo desde abajo. En las dos partes centrales la interpretación es doble, al margen de los humanos, lagartijas y lorapotes.
Toda imagen de la realidad es una proyección sobre la superficie plana de esa realidad. Cualquier figura de superficie launa no tiene por qué ser la proyección de la realidad tridimensional. Es el caso de Belvedere, 1958, en la litografía, que nos da la solución el propio cuadro [2]. La clave está en esa especie de cubo que tiene el chico que aparece sentado en él (figura 3). Veamos los cubos adyacentes. En la primera tenemos dos opciones, dependiendo de que los vértices 1 y 4 estén más o menos cerca de nosotros que los vértices 2 y 3. Asimismo, los vértices 2 y 4 podrían verse más cerca que el resto, a pesar de contravenir nuestra idea de cubo en nuestra mente. Si damos volumen a los bordes del cubo, entre otras cosas, podríamos conseguir “cubos” b y c, en contra de lo que nuestros sentidos tienen (figura 4).
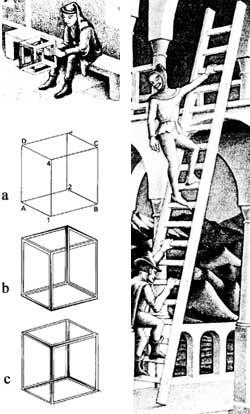

En Belvedere podemos ver a la vez la escalera interior y exterior. La dirección del eje longitudinal del piso superior es la que ve la mujer. La de abajo, la del hombre, que forma un ángulo recto. Las columnas que unen el primer y segundo piso, salvo las de los extremos, unen los lados anterior y posterior, es decir, están en diagonal y no verticales. La imagen se puede dividir horizontalmente en dos, siendo las partes superior e inferior rectas (edificables). Sin embargo, ambas no pueden existir simultáneamente.
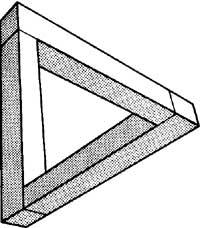
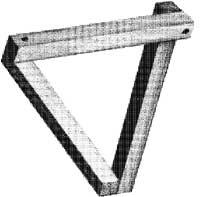
R. representadas en las figuras 5 y 6. La litografía Cascada de Escher (1961) fue sugerida por “tribar” de Penrose. La tribarra, al igual que los cubos anteriores, no se puede construir en tres dimensiones. Si en “Salto de agua” nos fijamos sólo en el agua, empezando por el turtuco, a lo largo del canal, el agua se va alejando hacia la derecha, luego hacia la izquierda, hacia la derecha de nuevo y por último hacia la izquierda, para salir al turco. Este tribar y salto de agua producen el mismo efecto (Figura 7).


Se basó en otra imagen de Penrose para la litografía de la Escalera de Escher, arriba, abajo, 1960 (Figura 8). En esta imagen quiso explicar la idea del infinito. Para ello se utilizó la escalera que siempre sube (o baja) de Penros. Si seguimos a los personajes que están en el exterior, aunque siempre subamos, después de dar una vuelta completa nos daremos cuenta de que se encuentran en el mismo lugar. La trampa queda al descubierto si cortamos el edificio en sierras horizontales. La primera capa se encuentra a un nivel inferior al resto, es decir, las capas no están superpuestas, sino que forman un espiral.
En la figura 9 se puede observar, en plano horizontal, cómo se puede obtener una escalera en continuo ascenso (9 a, c). Pero esta solución tiene un problema. Se pierde perspectiva, ya que los puntos de escape, V1 y V2, quedan bajo el bautizo. Esto puede resolverse si se alarga a dos caras (9 d). El dibujo de Escher nos indica que esta solución es válida.
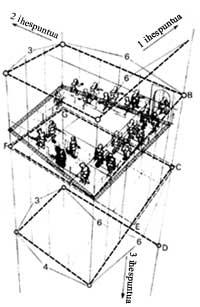
Sabemos cómo nos engaña la imagen: la escalera se encuentra en un plano horizontal, mientras que el resto de detalles de la imagen (plintos de columnas, marcos de ventanas, etc.) se adelantan en forma de espiral. Si trazamos rectas verticales en cada nivel, observamos que estas líneas forman un prisma de proporciones 6:6:3:4. Todos los puntos de la imagen situados a la misma altura forman un espiral (línea de punto) (Figura 10).
Aproximación al infinito
En un artículo escrito en 1959, Escher afirmó literalmente lo que motivaba a representar el infinito: “Es imposible pensar que no hay nada más allá de las estrellas más lejanas que vemos en el horizonte. (…). Por eso, desde que el hombre está en el suelo (de pie, sentado o tumbado, corre, navega, va a caballo y vuela), más allá de la presencia del purgatorio, el cielo y el infierno, mantenemos la idea de la transmigración y la mía, todos ellos espacios de infinito ancho o estados de infinita duración en el tiempo”.
Con la partición regular de la superficie todavía no se ha conseguido el infinito, sino sólo parte de ella. Pero la habilidad de Escher en la partición regular de la superficie le resultó muy útil. Sin embargo, se necesitaba un elemento nuevo: una estructura que permitiera representar la superficie infinita en una superficie finita.
En 1937 realiza su primera sesión utilizando imágenes congruentes. En 1939 utilizó imágenes uniformes, pero la idea de la metamorfosis seguía predominando. Sólo desde 1955 utilizó imágenes uniformes para formar series que sugieren infinito. Estos trabajos se pueden dividir en tres secciones, dependiendo de la estructura que hay debajo de la imagen: imágenes cuadradas, imágenes espirales y las imágenes sugeridas por Coxeter.
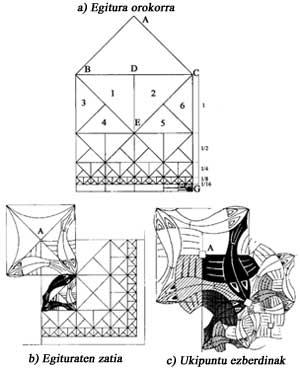
La figura 11 a muestra una solución al problema de representación del infinito. Si la diferencia del cuadrado EFCD es de 10 cm, la parte inferior será de 5 cm, y la siguiente de 2,5 cm, etc. CG 20 cm, pero podemos ver infinitos cuadrados cada vez más pequeños. Escher utilizó esta estructura para ilustrar un manual sobre la partición regular de la superficie.

Limite cuadrado, 1964, dibujo en madera, con una estructura más compleja [3], pero basada en la anterior (Figura 11 b). Para comprender mejor la imagen, una vez conocida la infraestructura, explicaremos por qué aparecen tres colores. Observando los puntos en los que los peces se tocan, observaremos que son de tres tipos (Figura 11 c). En el punto A se recogen cuatro aletas de cuatro peces, en el punto B cuatro cabezas y cuatro colas, y en el punto C tres aletas. En los puntos A y B no se necesita más de dos colores. En el punto C son necesarios tres colores. Los puntos A sólo están en diagonales. Por último, los colores que se recogen en los puntos A y B aparecen en diferentes combinaciones.
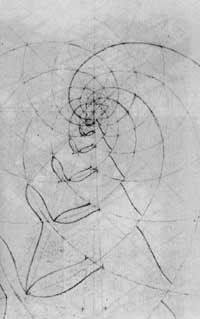
La estructura que se encuentra debajo de las figuras de las espirales es una espiral logarítmica. Este concepto matemático no lo conocía Escher y lo descubrió de la siguiente manera (Figura 12): representó las primeras circunferencias concéntricas, disminuyendo las distancias entre ellas hacia el centro. Luego trazó los radios que dividían las circunferencias en los mismos arcos. Partiendo de un punto de la circunferencia exterior, marcó los puntos que cortan los radios y las circunferencias para que una vez unidos formaran la espiral.
Su trayectoria vital I, 1958, empleó doble espiral que partía de 8 puntos de la circunferencia. En Trayectoria vital II, 1958, los puntos de partida son cuatro y en Trayectoria vital III, 1966, doce espirales parten de 6 puntos.

La trayectoria vital II muestra que dos espirales que parten de dos puntos diferentes de la circunferencia están unidas desde el exterior. De este modo, se puede llegar hasta el centro desde el límite exterior y de ahí volver al punto de partida (Figura 13). En la imagen se puede ver el espiral roja hacia el centro y el espiral azul que sale del centro, coincidentes en su parte exterior.
En Ubila, 1957, el dibujo era anterior al ciclo de vida y no había agotado todas las posibilidades [4]. En las zonas superior e inferior aparecen dos espirales que se desplazan en la misma dirección. Las espirales se han dibujado por la espalda de dos peces en sentido contrario. Sólo se han utilizado dos planchas de impresión. Para la representación de los peces grises y rojos superiores se han utilizado las dos láminas de peces inferiores rojos y grises.
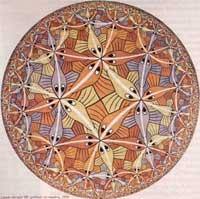
Para representar la serie de limite circular, Escher H. Se basó en el modelo utilizado por el matemático Poincare para representar la geometría parabólica. Modelo HSM Lo encontró en un libro de Coxeter (figura 14). Así nació el Limite circular de 1958 I (poco trabajo). En Limite circular II, similar al anterior, sustituyó a los peces por cruces. El limite circular IV, 1960, también se basa en la imagen de Coxeter. En cambio, Limite circular III, 1959 modificó la infraestructura [5]. Según el propio Escher: “Los errores del primero se han eliminado en la medida de lo posible. En esta ocasión, todos los peces de una serie tienen el mismo color y van tras el bautizo, que van creciendo a medida que se acercan al centro. (…). Ningún componente afecta al límite ....


La serpiente, 1969, dibujó en madera antes de sufrir una complicada operación [6]. A pesar de tener 71 años, la mano no vibró en su último trabajo. En la disputa por expresar el infinito se aprecia una mayor humildad (en las figuras anteriores, con ayuda de una lupa, dibujó figuras que medían menos de medio milímetro). La serpiente no acabó con la serie de pequeños anillos.
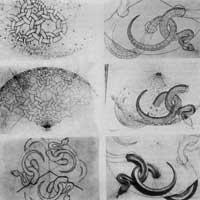
Cuando sugirió una disminución continua de tamaño lo abandonó (Figura 15). En los bocetos percibimos la infraestructura de Coxeter desde los grandes anillos hacia fuera. Pero consigue el mismo efecto hacia dentro, creando una línea ondulada. Las serpientes, tras ver muchas fotos, las representó de memoria. Estudios previos ponen de manifiesto la pulcritud de Escher por cada detalle. Esa fue una de las características de Escher.
Hemos visto la vida y el trabajo de Escher. Utilizó muchas estructuras matemáticas sin saberlo. Por eso hemos traído a esta sección a este ilustrador. A pesar de que Escher murió hace 20 años, nos dejó su trabajo. ¡Disfrútalos!






