Maurits Cornelis Escher (eta III)
Ezinezko munduak
Ezinezko munduen gaia ere tratatu zuen Escherrek. Zenbait irudi aipatu baino lehen, adibide batekin azter dezagun irudi horien funtsa (1. irudia). Irudian erronbo eta karratu bana itsatsirik ikus daiteke eta irudi guztiak berdinak dira itzala izan ezik. Goiko eta beheko irudiak bi eratara uler daitezke bertan adierazten denez. Gauza bera gertatzen da ikusten dugun guztiarekin. Gertatzen dena honakoa da: konturatu gabe ikusten dugun xehetasun askok nahastu ezinezko interpretazioa izatea. Hauek gabe argiaren intzidentzi angeluak interpretazio ezberdinak sortzen dituela ikusiko genuke.
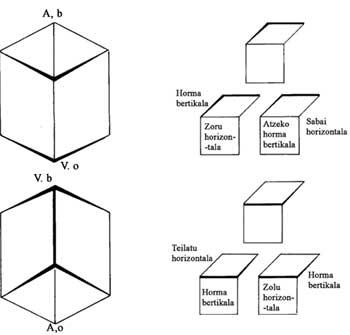

Ahurra eta ganbila irudian ojiba-gangazko tenplu kubikoek elementu arkitektoniko nagusiena osatzen dute [1]. Horregatik irudikatu ditugu aldameneko kuboak, bi interpretazio emanez (2. irudia). Ikusi bezain laster nabaritzen da irudiaren simetria; Erdiko iragapena ez da bapatekoa; mailakakoa baizik. Baina erdia pasa eta gero goia behe bihurtzen da eta aurrea atze bilakatzen da. Gizakiek, sugandilek eta lorapoteek, aldiz, inbertsioari aurre egiten diote. Hala ere, aldez (ezkerretik eskuinera edo alderantziz) aldatu nahiko balute garesti ordainduko lukete. Esate baterako, ezkerreko beheko aldean eskaileran igotzen ari denak tenpluari buelta eman, eserita dagoenaren aurretik pasa, erdian dagoen maskorra pasa eta aurrean dituen eskaileretan igo nahiko balu, izutu egingo litzateke bere oinetan zegoen eskailera sabai bihurtu dela konturatuta. Gauza bera gertatuko litzaieke ezker aldean dauden pertsonaia guztiei.

Harrigarria da bi dultzainarien artean dagoen ganga. Ezkerrekoarentzat teilatua den bitartean, hots, berak gainera jauzi egin lezake, eskuinekoarentzat sabaia da, hau da, jauzi eginez gero lurreraino eroriko litzateke.

2. irudian koadroa lau zatitan banatu da. Ezkerreko aldeak arkitektura ganbila dauka, puntu guztiak goitik ikusiko bagenitu bezala. Eskuineko aldean arkitektura ahurra erabiltzen da, hots, dena behetik ikusten dugu. Erdiko bi zatietan interpretazioa bikoitza da, gizakiak, sugandilak eta lorapoteak alde batera utzita.
Errealitateko irudi oro, errealitate horren gainazal launarekiko proiekzioa da. Gainazal launeko irudi orok berriz, ez du hiru dimentsioko errealitatearen proiekzioa zertan izan behar. Belvedere, 1958, litografian hori gertatzen da, soluzioa koadroak berak ematen digularik [2]. Bertan eserita agertzen den mutilak eskuetan duen kubo antzeko horretan datza gakoa (3. irudia). Ikus ditzagun aldameneko kuboak. Lehenengoan bi aukera ditugu, 1 eta 4 erpinak guregandik 2 eta 3 erpinak baino urrunago edo hurbilago egotearen arabera. Halaber, 2 eta 4 erpinak besteak baino gertuago ikus litezke, gure buruan kuboaz dugun ideiari kontra egin arren. Kuboaren ertzei bolumena ematen badiegu, besteak beste b eta c “kuboak” lor genitzake, gure zentzuek diotenaren kontra (4. irudia).
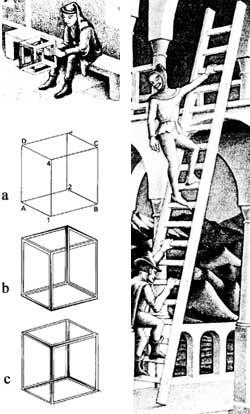

Belvedere lanean, aldi berean barruan eta kanpoan dagoen eskailera ikus dezakegu. Goiko pisuaren luzetarako ardatzaren norabidea emakumeak ikusten duenarena da. Behekoarena berriz, gizonak duena, biek angelu zuzena osatzen dutelarik. Lehenengo eta bigarren pisuak lotzen dituzten zutabeek, muturretakoek izan ezik, aurreko eta atzeko aldeak lotzen dituzte, hots, diagonalean daude, eta ez bertikal. Irudia bitan zati daiteke horizontalean, goiko eta beheko zatiak zuzenak (eraikigarriak) izanik. Hala ere, biak batera ezin dira existitu.
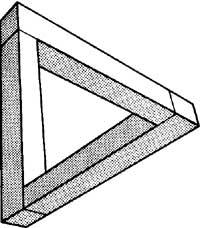
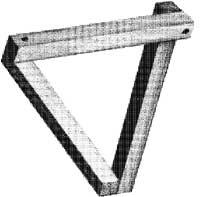
5. eta 6. irudietan ikus daitezkeen R. Penrose-ren “tribar”ek iradoki zion Escherri Urjauzia (1961) litografia. Tribarra, agerian dagoenez, aurreko kuboak bezalaxe ezin da hiru dimentsiotan eraiki. “Urjauzia” lanean uretan soilik fijatzen bagara, turtukitik hasiz, ubidean zehar, ura urrunduz doa eskuinera, gero ezkerrera, eskuinera berriro eta azkenik ezkerrera, hortik turtukira jauzteko. Efektu bera sortzen dute tribar eta urjauzi honek (7. irudia).


Penroseren beste irudi batean oinarritu zen Escher Eskaileran gora, eskaileran behera, 1960, litografia egiteko (8. irudia). Irudi honetan infinituaren ideia azaldu nahi izan zuen. Horretarako beti gora (edo behera) doan eskaileraz (Penroserenaz) baliatu zen. Kanpo aldean dauden pertsonaiei jarraitzen bagatzaizkie beti gora joan arren, buelta oso bat eman eta gero leku berean aurkitzen direla konturatuko gara. Amarrua agerian geratuko da eraikina zerrada horizontaletan ebakitzen badugu. Lehenengo geruza besteak baino maila baxuagoan dago, hau da, geruzak ez daude gainjarrita; kiribila osatzen dutela baizik.
9. irudian ikus daiteke, plano horizontalean, etengabe gora doan eskailera (9 a, c) nola lor daitekeen. Baina soluzio honek arazo bat dauka. Perspektiba galtzen da; ihes-puntuak, V1 eta V2, batabestearen azpian geratzen bait dira. Hau bi alde luzatuz gero (9 d) konpon daiteke. Escherren marrazkiak soluzio honek balio duela diosku.
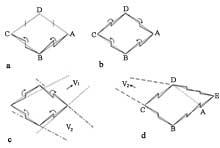
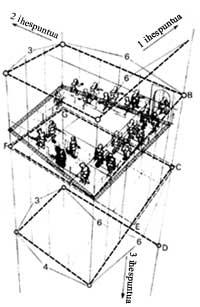
Badakigu irudiak nola engainatzen gaituen: eskailera plano horizontal batean dago, bitartean irudiko beste xehetasunak (zutabeen plintoak, leihoen markoak, etab.) kiribil itxuraz aurreratzen dira. Maila bakoitzean zuzen bertikalak marratzen baditugu, lerro hauek 6:6:3:4 proportzioetako prisma osatzen dutela ohartuko gara. Altuera berberean dauden irudiko puntu guztiek kiribil bat osatzen dute (puntuzko lerroa) (10. irudia).
Infinituranzko hurbilketa
1959an idatzitako artikulu batetan Escherrek hitzez adierazi zuen infinitua errepresentatzera zerk motibatzen zuen: “Ezinezkoa zaigu ortzean ikusten ditugun izar urrunenak baino harantzago ezer ez dagoela pentsatzea. (....). Horregatik, gizakia lurrean dagoenetik (zutik, eserita edo etzanda dagoenetik, korrika egin, nabigatu, zaldiz joan eta hegaz egiten duenetik) harantzagokoa, purgatorioa, zerua eta ifernua egoteari, transmigrazio eta nirbanaren ideiari eusten diogu, guztiak espazioz zabalera infinituko lekuak edo denboraz iraupen infinituko estatuak direlarik”.
Gainazalaren partiketa erregularrarekin ez da oraindik infinitua lortu; bere zati bat soilik baizik. Baina Escherrek gainazalaren partiketa erregularrean lortu zuen trebetasuna oso baliagarria gertatu zitzaion. Hala ere, elementu berri bat behar zen: gainazal infinitua gainazal finitu batean errepresentatzeko modua eskaintzen duen egitura.
1937an lehenengo saioa egin zuenean, irudi kongruenteak erabili zituen. 1939an irudi uniformeak erabili zituen, baina metamorfosiaren ideia zen artean nagusi. 1955. urteaz geroztik soilik erabili zituen irudi uniformeak infinitua iradokitzen duten serieak osatzeko. Lan hauek hiru sailetan bana daitezke, irudiaren azpian dagoen egituraren arabera: irudi karratuak, irudi kiribilak eta Coxeterrek iradokitako irudiak sailetan.
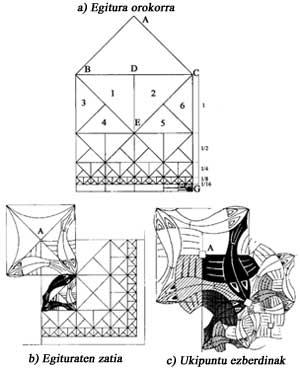
11 a irudian infinitua adierazteko problemaren soluzio bat ikus daiteke. EFCD karratuaren aldea 10 cm-koa bada, azpian dagoenarena 5 cm-koa izango da, eta hurrengoa 2,5 cm-koa, etab. CG 20 cm-koa izango da, baina, gero eta txikiago diren infinitu karratu ikus dezakegu. Escherrek gainazalaren partiketa erregularrari buruzko eskuliburu bat ilustratzeko erabili zuen egitura hau.

Limite karratua, 1964, zurean egindako marrazkiak, egitura konplexuagoa dauka [3], baina aurrekoan oinarriturik dago (11 b irudia). Irudia hobeto ulertzeko, azpiegitura ezagutu eta gero, hiru kolore zergatik agertzen diren azalduko dugu. Arrainek elkar jotzen duteneko puntuei begiratuz, hiru eratakoak direla konturatuko gara (11 c irudia). A puntuan lau arrain ezberdinen lau hegal biltzen dira, B puntuan lau buru eta lau isats, eta C puntuan hiru hegal. A eta B puntuetan bi kolore baino gehiago ez da behar. C puntuan, aldiz, hiru kolore behar dira. A puntuak diagonaletan bakarrik daude. Azkenik, A eta B puntuetan biltzen diren koloreak konbinazio ezberdinetan agertzen direla esango dugu.
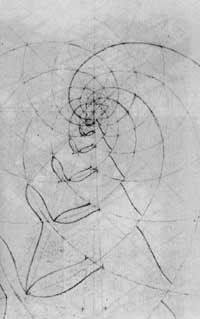
Kiribilen irudien azpian dagoen egitura, kiribil logaritmikoa da. Kontzeptu matematiko hau ez zuen Escherrek ezagutzen eta honela aurkitu zuen (12. irudia): lehenengo zenbait zirkunferentzia zentrukide irudikatu zuen, beren arteko distantziak zentrurantz hurbildu ahala txikiagotuz. Gero zirkunferentziak arku berdinetan zatitzen zituzten erradioak marraztu zituen. Kanpoko zirkunferentziako puntu batetik abiatuz, erradioek eta zirkunferentziek elkar ebakitzen duten puntuak markatu zituen, lotutakoan kiribilerdia osa zezaten.
Bizi-ibilbidea I, 1958, lanean zirkunferentziako 8 puntutatik abiatzen ziren kiribil bikoitzak erabili zituen. Bizi-ibilbidea II, 1958, lanean abiapuntuak lau dira eta Bizi-ibilbidea III, 1966, lanean hamabi kiribilak 6 puntutatik abiatzen dira.

Bizi-ibilbidea II lanean zirkunferentziako bi puntu ezberdinetatik abiatzen diren bi kiribil kanpotik lotura dutela ikus daiteke. Horrela, zentruraino ailega daiteke kanpoko limitetik eta hortik abiapuntura itzuli (13. irudia). Irudian zentrurantz doan kiribil gorria eta zentrutik ateratzen den kiribil urdina ikus daitezke, kanpo aldean bat datozelarik.
Ubila, 1957, marrazkia bizi-zikloak baino lehenagokoa zen eta bertan ez zituen aukera guztiak agortu [4]. Goiko eta beheko aldeetan norabide berean higitzen diren bi kiribil agertzen dira. Kiribilak kontrako norantzan dabiltzan bi arrainen bizkarretik marratu dira. Inprimatzeko bi xafla besterik ez dira erabili. Goiko arrain gris eta gorriak irudikatzeko beheko arrain gorri eta grisen bi xaflak erabili dira.
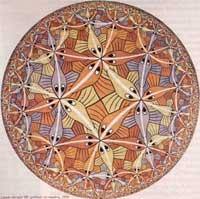
Limite zirkularren seriea irudikatzeko, Escher H. Poincare matematikariak geometria parabolikoa adierazteko erabili zuen ereduan oinarritu zen. Eredu hau H.S.M. Coxeter-en liburu batean aurkitu zuen (14. irudia). Horrela sortu zen 1958ko Limite zirkularra I (ez da oso lan ona). Limite zirkularra II lanean, aurrekoaren antzekoa denean, arrainen ordez gurutzeak irudikatu zituen. Limite zirkularra IV, 1960, ere, Coxeterren irudian oinarritzen da. Limite zirkularra III, 1959, lanean aldiz, azpiegitura aldatu egin zuen [5]. Escher berak zioenez: “Lehenengoaren akatsak ezabatu egin dira, ahal den neurrian. Oraingoan, serie bateko arrain guztiek kolore bera daukate eta batabestearen atzetik doaz, zentrura hurbildu ahala handituz doazelarik. (....). Osagai batek ere ez du limitea ukitzen ....


Sugeak, 1969, zurean egindako marrazkia ebakuntza zail bat jasan baino lehen egin zuen [6]. 71 urte izan arren, eskuak ez zion dardar egin bere azken lan honetan. Infinitua adierazteko lehian apaltasun handiagoa nabari zaio (aurreko irudietan lupa baten laguntzaz milimetroerdia baino gutxiago neurtzen zuten irudiak marraztu zituen). Sugeak lanean eraztun txikien seriea ez zuen bukatu.
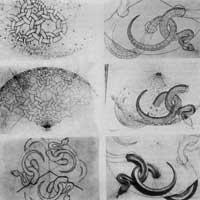
Tamainaren etengabeko txikiagotzea iradoki zuenean utzi egin zuen (15. irudia). Zirriborroetan Coxeterren azpiegitura sumatzen dugu eraztun handietatik kanporantz. Baina efektu bera lortzen du barrurantz, lerro uhinkatua sortuz. Sugeak, argazki ugari ikusi eta gero buruz irudikatu zituen. Aurretiko estudioek agerian uzten dute Escherrek xehetasun bakoitza lantzeko zuen txukuntasuna. Hori izan zen Escherren ezaugarrietako bat.
Escherren bizitza eta lana ikusi dugu. Matematikako egitura ugari erabili zuen berak jakin gabe. Horregatik ekarri dugu sail honetara irudigile hau. Escher duela 20 urte hil zitzaigun arren, bere lana utzi zigun. Ikus eta goza dezagun!







