Maurits Cornelis Escher (i III)
Mons impossibles
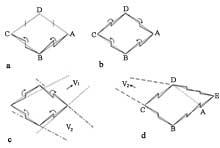
També va tractar el tema de mons impossibles. Abans d'esmentar algunes imatges, analitzem amb un exemple l'essència de les mateixes (figura 1). En la imatge es pot veure un rombe i un quadrat pegats i totes les imatges són iguals excepte l'ombra. Les figures superior i inferior poden entendre's de dues formes, segons s'indica en elles. El mateix ocorre amb tot el que veiem. El que passa és que molts detalls que veiem sense adonar-nos tenen una interpretació inconfusible. Sense ells l'angle d'incidència de la llum genera diferents interpretacions.
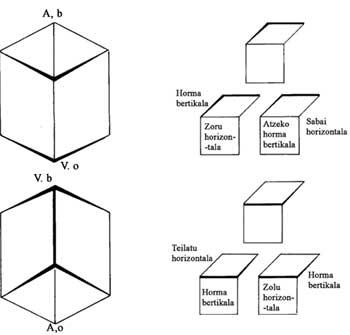

En la imatge còncava i convexa, els temples cúbics ogivals formen l'element arquitectònic més important [1]. Per això hem representat els cubs adjacents amb dues interpretacions (figura 2). Tan aviat com es veu s'aprecia la simetria de la imatge; el filtrat central no és brusc, sinó escalonat. Però després de la meitat, la part superior es torna baixa i la davantera es converteix en posterior. Els éssers humans, sargantanes i lorapotes, per part seva, s'enfronten a la inversió. No obstant això, si volguessin canviar de part (d'esquerra a dreta o viceversa) pagarien car. Per exemple, si el que està pujant per l'escala en la part inferior esquerra volgués donar la volta al temple, passar per davant de l'asseguda, passar la petxina central i pujar per les escales que té davant, s'espantaria en adonar-se que l'escala que estava als seus peus s'ha convertit en un sostre. El mateix passaria a tots els personatges que estan a l'esquerra.

És sorprenent la volta situada entre els dos dolçainers. Mentre que per al de l'esquerra és la teulada, és a dir, ell pot saltar, per al de la dreta el sostre és el sostre, és a dir, si saltés cauria fins al sòl.

En la figura 2 s'ha dividit el quadre en quatre parts. La part esquerra té una arquitectura convexa, com si poguéssim veure tots els punts des de dalt. En la part dreta s'utilitza l'arquitectura còncava, és a dir, ho veiem tot des de baix. En les dues parts centrals la interpretació és doble, al marge dels humans, sargantanes i lorapotes.
Tota imatge de la realitat és una projecció sobre la superfície plana d'aquesta realitat. Qualsevol figura de superfície launa no té per què ser la projecció de la realitat tridimensional. És el cas de Belvedere, 1958, en la litografia, que ens dóna la solució el propi quadre [2]. La clau està en aquesta espècie de cub que té el noi que apareix assegut en ell (figura 3). Vegem les galledes adjacents. En la primera tenim dues opcions, depenent del fet que els vèrtexs 1 i 4 estiguin més o menys prop de nosaltres que els vèrtexs 2 i 3. Així mateix, els vèrtexs 2 i 4 podrien veure's més a prop que la resta, malgrat contravenir la nostra idea de cub en la nostra ment. Si donem volum a les vores del cub, entre altres coses, podríem aconseguir “cubs” b i c, en contra del que els nostres sentits tenen (figura 4).
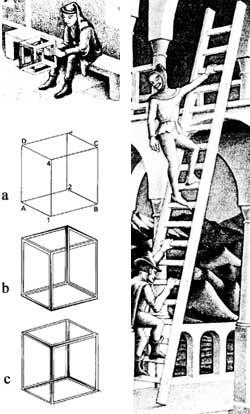

En Belvedere podem veure alhora l'escala interior i exterior. La direcció de l'eix longitudinal del pis superior és la que veu la dona. La de baix, la de l'home, que forma un angle recte. Les columnes que uneixen el primer i segon pis, excepte les dels extrems, uneixen els costats anterior i posterior, és a dir, estan en diagonal i no verticals. La imatge es pot dividir horitzontalment en dues, sent les parts superior i inferior rectes (edificables). No obstant això, ambdues no poden existir simultàniament.
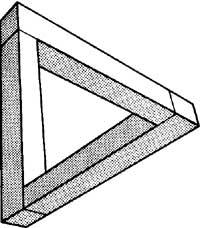
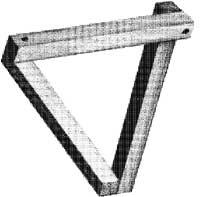
R. representades en les figures 5 i 6. La litografia Trencada d'Escher (1961) va ser suggerida per “tribar” de Penrose. La tribarra, igual que els cubs anteriors, no es pot construir en tres dimensions. Si en “Salt d'aigua” ens fixem només en l'aigua, començant pel turtuco, al llarg del canal, l'aigua es va allunyant cap a la dreta, després cap a l'esquerra, cap a la dreta de nou i finalment cap a l'esquerra, per a sortir al turc. Aquest tribar i salt d'aigua produeixen el mateix efecte (Figura 7).


Es va basar en una altra imatge de Penrose per a la litografia de l'Escala d'Escher, a dalt, a baix, 1960 (Figura 8). En aquesta imatge va voler explicar la idea de l'infinit. Per a això es va utilitzar l'escala que sempre puja (o baixa) de Penros. Si seguim als personatges que estan en l'exterior, encara que sempre pugem, després de fer un volt completa ens adonarem que es troben en el mateix lloc. El parany queda al descobert si tallem l'edifici en serres horitzontals. La primera capa es troba a un nivell inferior a la resta, és a dir, les capes no estan superposades, sinó que formen un espiral.
En la figura 9 es pot observar, en pla horitzontal, com es pot obtenir una escala en continu ascens (9 a, c). Però aquesta solució té un problema. Es perd perspectiva, ja que els punts de fuita, V1 i V2, queden sota el bateig. Això pot resoldre's si s'allarga a dues cares (9 d). El dibuix d'Escher ens indica que aquesta solució és vàlida.
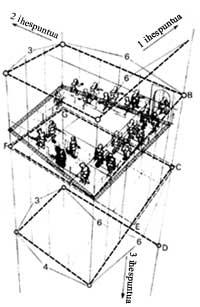
Sabem com ens enganya la imatge: l'escala es troba en un pla horitzontal, mentre que la resta de detalls de la imatge (plints de columnes, marcs de finestres, etc.) s'avancen en forma d'espiral. Si tracem rectes verticals en cada nivell, observem que aquestes línies formen un prisma de proporcions 6:6:3:4. Tots els punts de la imatge situats a la mateixa altura formen un espiral (línia de punt) (Figura 10).
Aproximació a l'infinit
En un article escrit en 1959, Escher va afirmar literalment el que motivava a representar l'infinit: “És impossible pensar que no hi ha res més enllà de les estrelles més llunyanes que veiem en l'horitzó. (…). Per això, des que l'home està en el sòl (dempeus, assegut o tombat, corre, navega, va a cavall i vola), més enllà de la presència del purgatori, el cel i l'infern, mantenim la idea de la transmigració i la meva, tots ells espais d'infinit ample o estats d'infinita durada en el temps”.
Amb la partició regular de la superfície encara no s'ha aconseguit l'infinit, sinó només part d'ella. Però l'habilitat d'Escher en la partició regular de la superfície li va resultar molt útil. No obstant això, es necessitava un element nou: una estructura que permetés representar la superfície infinita en una superfície finita.
En 1937 realitza la seva primera sessió utilitzant imatges congruents. En 1939 va utilitzar imatges uniformes, però la idea de la metamorfosi continuava predominant. Només des de 1955 va utilitzar imatges uniformes per a formar sèries que suggereixen infinit. Aquests treballs es poden dividir en tres seccions, depenent de l'estructura que hi ha sota la imatge: imatges quadrades, imatges espirals i les imatges suggerides per Coxeter.
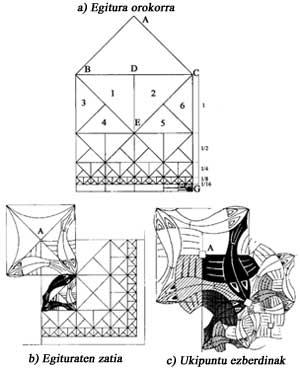
La figura 11 a mostra una solució al problema de representació de l'infinit. Si la diferència del quadrat EFCD és de 10 cm, la part inferior serà de 5 cm, i la següent de 2,5 cm, etc. CG 20 cm, però podem veure infinits quadrats cada vegada més petits. Escher va utilitzar aquesta estructura per a il·lustrar un manual sobre la partició regular de la superfície.

Limiti quadrat, 1964, dibuix en fusta, amb una estructura més complexa [3], però basada en l'anterior (Figura 11 b). Per a comprendre millor la imatge, una vegada coneguda la infraestructura, explicarem per què apareixen tres colors. Observant els punts en els quals els peixos es toquen, observarem que són de tres tipus (Figura 11 c). En el punt A se recullen quatre aletes de quatre peixos, en el punt B quatre caps i quatre cues, i en el punt C tres aletes. En els punts A i B no es necessita més de dos colors. En el punt C són necessaris tres colors. Els punts A només estan en diagonals. Finalment, els colors que es recullen en els punts A i B apareixen en diferents combinacions.
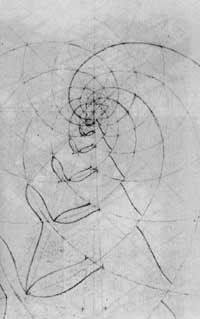
L'estructura que es troba sota les figures de les espirals és una espiral logarítmica. Aquest concepte matemàtic no el coneixia Escher i ho va descobrir de la següent manera (Figura 12): va representar les primeres circumferències concèntriques, disminuint les distàncies entre elles cap al centre. Després va traçar els radis que dividien les circumferències en els mateixos arcs. Partint d'un punt de la circumferència exterior, va marcar els punts que tallen els radis i les circumferències perquè una vegada units formessin l'espiral.
La seva trajectòria vital I, 1958, va emprar doble espiral que partia de 8 punts de la circumferència. En Trajectòria vital II, 1958, els punts de partida són quatre i en Trajectòria vital III, 1966, dotze espirals parteixen de 6 punts.

La trajectòria vital II mostra que dues espirals que parteixen de dos punts diferents de la circumferència estan unides des de l'exterior. D'aquesta manera, es pot arribar fins al centre des del límit exterior i d'aquí tornar al punt de partida (Figura 13). En la imatge es pot veure l'espiral vermella cap al centre i l'espiral blava que sali del centre, coincidents en la seva part exterior.
En Ubila, 1957, el dibuix era anterior al cicle de vida i no havia esgotat totes les possibilitats [4]. En les zones superior i inferior apareixen dues espirals que es desplacen en la mateixa direcció. Les espirals s'han dibuixat per l'esquena de dos peixos en sentit contrari. Només s'han utilitzat dues planxes d'impressió. Per a la representació dels peixos grisos i vermells superiors s'han utilitzat les dues làmines de peixos inferiors vermells i grisos.
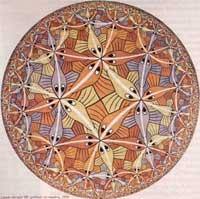
Per a representar la sèrie de limiti circular, Escher H. Es va basar en el model utilitzat pel matemàtic Poincare per a representar la geometria parabòlica. Model HSM Ho va trobar en un llibre de Coxeter (figura 14). Així va néixer el Limiti circular de 1958 I (poc treball). En Limite circular II, similar a l'anterior, va substituir als peixos per creus. El limiti circular IV, 1960, també es basa en la imatge de Coxeter. En canvi, Limiti circular III, 1959 va modificar la infraestructura [5]. Segons el propi Escher: “Els errors del primer s'han eliminat en la mesura que sigui possible. En aquesta ocasió, tots els peixos d'una sèrie tenen el mateix color i van després del bateig, que van creixent a mesura que s'acosten al centre. (…). Cap component afecta al límit ....


La serp, 1969, va dibuixar en fusta abans de sofrir una complicada operació [6]. Malgrat tenir 71 anys, la mà no va vibrar en el seu últim treball. En la disputa per expressar l'infinit s'aprecia una major humilitat (en les figures anteriors, amb ajuda d'una lupa, va dibuixar figures que mesuraven menys de mig mil·límetre). La serp no va acabar amb la sèrie de petits anells.
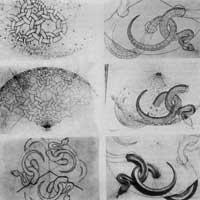
Quan va suggerir una disminució contínua de grandària ho va abandonar (Figura 15). En els esbossos percebem la infraestructura de Coxeter des dels grans anells cap a fora. Però aconsegueix el mateix efecte cap a dins, creant una línia ondulada. Les serps, després de veure moltes fotos, les va representar de memòria. Estudis previs posen de manifest la netedat d'Escher per cada detall. Aquesta va ser una de les característiques d'Escher.
Hem vist la vida i el treball d'Escher. Va utilitzar moltes estructures matemàtiques sense saber-ho. Per això hem portat a aquesta secció a aquest il·lustrador. A pesar que Escher va morir fa 20 anys, ens va deixar el seu treball. Gaudeix-los!






