Ajudant de Matemàtiques
Johann Radon (1887-1956) i idea matemàtica
Johann Radon va néixer en 1887 en Tetschen (Bohèmia), actualment Decin, República Txeca. Va estudiar Matemàtiques en la Universitat de Viena i, després de ser professor en diverses universitats alemanyes, va tornar a Viena en 1947, on va morir com a professor en 1956. És conegut pels matemàtics, que va abandonar importants treballs, especialment en la teoria de la integració.
A pesar que no és tan conegut, el resultat que sustenta la tomografia se situa en Radó, precedit per un article de 1917. En termes tècnics, una versió del bell teorema de Radó podria expressar-se com: una funció donada en el pla pot recuperar-se mitjançant integrals (unidimensional) realitzades sobre totes les rectes. I coneixent aquestes integrals, també va donar una fórmula per a recuperar la funció. Sense espantar més al lector que se sent perdut entre aquests termes matemàtics, veurem un exemple senzill.
Suposem que en el pla tenim un conjunt tancat amb dos orificis en el seu interior, com a mostra la imatge. Estant fora del pla i mirant sense obstacles, com a feixos en llegir aquesta pàgina, no tens problemes per a veure els forats interiors. Però la formiga que viu sobre el paper i no pot aixecar el cap del paper només pot descriure el límit exterior que envolta al conjunt. Com sabrà que dins hi ha dos forats? De la mateixa manera, si hi hagués una paret en el límit exterior del conjunt, els nostres ulls no podrien veure la part interior i estaríem en el mateix estat de la formiga, coneixent l'aresta, però sense cap informació de l'interior. En què consisteix el teorema de Radó? "Si em dóna la longitud que dóna cada línia recta en tallar el conjunt, us definiré completament el conjunt" ens diu Radó, ja que permet descriure tots els límits exteriors i interiors. (Prenent sobre el conjunt una funció que val 1 i fora i 0 en els orificis, la integral sobre una recta és la longitud indicada.) Hem modificat el problema, ara necessitaríem longituds de tall, però sembla que per a calcular les longituds cal conèixer l'interior. Estem en una roda boja?
Allan Cormack (1924-1998) i la solució teòrica
Allan Cormack va néixer a Johannesburg (Sud-àfrica) en 1924, fill de funcionaris escocesos. Va començar els seus estudis d'Enginyeria en la Universitat de la Ciutat del Cap, però finalment va decidir canviar a Física. Durant la seva tesi doctoral en el prestigiós Laboratori Cavendish de Cambridge, va estudiar una oferta universitària i va tornar a Sud-àfrica abans de finalitzar la tesi. Anys més tard es va traslladar a la Universitat d'Harvard per a realitzar la recerca i finalment va quedar als Estats Units com a professor i investigador de la Universitat de Tufts (Massachussets).
Segons ell, encara que l'interès per desenvolupar la tomografia computada es va despertar durant la seva estada a Sud-àfrica, va haver de treballar a Amèrica la Física nuclear i la Física de Partícules, i només ocasionalment va tenir ocasió d'analitzar el problema de la tomografia. No obstant això, el seu treball va ser fructífer i va exposar en dos articles publicats en 1963 i 1964 la base teòrica de la tomografia.
Mira una part del teu cos, com el genoll. Ho veus des de fora, però no des de dins. Suposem que un pla imaginari et travessa el genoll i estàs en la mateixa situació que l'exemple de l'apartat anterior, és a dir, el tall genera una imatge plana i només veus la línia exterior, no saps quina és l'estructura interna. Si poguéssim calcular "integrals"! Cormack aviat va entendre que es tractava d'un problema matemàtic que guanyaria si s'aconseguís una via pràctica de càlcul. Va trobar resposta en raigs X.
Els raigs X van ser descoberts per Röntgen en 1895 i es va considerar un tipus de radiació electromagnètica de menor longitud d'ona que la llum. Donada la seva propietat de travessar diversos objectes opacs a la llum, es va detectar la possibilitat d'obtenir unes "fotos" especials que van donar lloc a les radiografies tan utilitzades pels metges. Però igual que ocorre en les fotos, els objectes que es troben en diferents plans haurien d'aparèixer entre si en les radiografies, per la qual cosa l'anterior oculta la posterior. La tècnica de la tomografia és completament diferent, ja que, com el seu propi nom indica, cada imatge mostra un tall (tómos, grec), evitant superposicions.
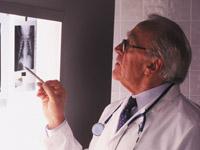
Els raigs X es propaguen en línies rectes i perden intensitat en el camí. Sent aquesta pèrdua proporcional a la intensitat, longitud del recorregut i densitat del mitjà, una equació matemàtica ens indica que per a obtenir la integral de la densitat n'hi ha prou amb conèixer les intensitats d'entrada i sortida. Com els mesuraments es realitzen en l'exterior, Cormack ens ha inventat un camí que faria possible la integral que demanàvem més amunt sense veure l'interior. A partir d'aquí la Matemàtica necessitava més inversió per a conèixer la funció o per a fer la imatge d'una manera més pràctica. A més, en el món real no és possible realitzar totes les integrals que exigeix la teoria, ja que apareixen infinits integrals i els mètodes d'aproximació també han de ser sol·licitats a les Matemàtiques.
Davant l'evident revolució que podia suposar la proposta de Cormack, per què no es va dur a terme immediatament i es va construir una eina que fes imatges? No hi ha respostes clares, però sembla que la capacitat dels ordinadors de llavors no era suficient per a realitzar tots els càlculs necessaris. Per això, després de la publicació dels articles, Cormack va abandonar el tema per a reprendre'l quan deu anys més tard el seu invent es va fer realitat.
Godfrey Hounsfield (1919) i primeres màquines
Godfrey Hounsfield va néixer en el comtat anglès de Nottinghamshire en 1919. La Segona Guerra Mundial es va celebrar en l'Exèrcit de l'Aire, sobretot en radars i radiocomunicacions. Després de la guerra va estudiar Enginyeria elèctrica a Londres i en 1951 es va incorporar a l'empresa EMI (Electric and Musical Industries), coneguda per a nosaltres com a discogràfica. Malgrat els inicis dels ordinadors, Hounsfield aviat es va proposar sobre aquest tema i en 1958 va construir el primer ordenador britànic en transistor amb el seu equip (EMIDEC 1100).
Anys més tard, després d'inviabilitat d'un projecte en el qual treballava, li van donar llibertat per a estudiar nous camps i va proposar treballar el reconeixement automàtic de formes. En aquesta línia, va desenvolupar la idea bàsica de l'OTA en 1967 i la va patentar a l'any següent. Quatre anys després es va construir la primera màquina (EMI-Scanner).
Com s'ha esmentat anteriorment, en la pràctica no és possible realitzar mesuraments (és a dir, “integrals”) sobre totes les rectes. Seleccionant algunes direccions d'un pla i emetent raigs paral·lels, es mesura la intensitat mitjançant uns sensors de cristall situats a l'altre costat. Les dades obtingudes són presos per l'ordinador i, resolent un munt d'equacions, ofereix una imatge aproximada de la intersecció del pla sobre el cos. El procés es repeteix amb una mica de moviment del pla i finalment s'aprecia l'estructura interna del cos mitjançant la visualització d'imatges de talls successius. El que hem dit en poques paraules suposa superar molts obstacles teòrics i pràctics perquè la imatge que dóna la màquina sigui fiable. A més del coneixement tècnic, Hounsfield és un reconeixement a la imaginació i a la intuïció. Sense utilitzar els mètodes de les matemàtiques i la capacitat de càlcul dels ordinadors no hauria estat possible canalitzar aquest invent.
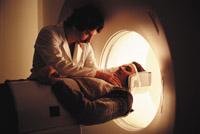
Allan Cormack i Godfrey Hounsfield van aconseguir el Premi Nobel de Medicina i Fisiologia de 1979 per la seva possible tomografia computada. A partir de llavors la tècnica ha anat evolucionant i les eines han millorat; si inicialment s'utilitzaven raigs paral·lels, ara s'emeten feixos de raigs des de diversos punts. D'altra banda, el creixement de la capacitat de càlcul dels ordinadors ha estat també positiu. Això ens porta a pensar que cada vegada amb mesures en més línies rectes s'aconsegueix una millor imatge. No obstant això, la pràctica té un límit: la salut dels éssers vius. No es poden fer circular raigs a través del cos, ja que existeix el risc de causar grans danys. En qualsevol cas, l'OTA ha obtingut un gran èxit i s'utilitza de manera massiva, no sols en l'àmbit mèdic.





