De la Terre à la Lune

D'abord, analysons si théoriquement, au moins, il est possible de tirer un projectile avec un canon et de ne pas tomber celui-ci sur la Terre. La théorie nous dit oui. Voyons les deux possibilités extrêmes. Dans la première d'entre elles, le tir se fera verticalement vers le haut et avec la Terre seule (ni air ni tout autre type de friction) il suffira de doter le projectile de l'énergie cinétique nécessaire pour sortir de l'influence de la Terre. Dans le cas où le calcul pas trop compliqué donne au projectile une vitesse de 12.386 km/s (ou plus), on peut observer que cela se produira.
Une autre option est de lancer le projectile horizontalement. Pourquoi, dans des cas normaux, le projectile at-il sur Terre? Car la terre tire vers le bas. Par conséquent, son parcours est celui de la ligne qui se penche vers le sol au lieu d'être rectiligne et finalement il rencontre avec lui. Il est vrai que la surface de la Terre est courbe, mais l'inclinaison de la trajectoire du projectile est beaucoup plus fermée que celle de la Terre. Si nous avons réduit l'inclinaison de la trajectoire du projectile et l'avons fait aussi grande que la surface de la Terre, le projectile ne tomberait jamais sur la Terre et continuerait à tourner autour d'elle, devenant le satellite de la Terre. Mais comment pouvez-vous obtenir? Comme avant, donnant au projectile la vitesse nécessaire.
Nous y avons la section d'un secteur de la sphère terrestre. Le canyon est situé au sommet A d'une montagne. Si la Terre n'avait aucune gravité, après une seconde de tir horizontal, le projectile serait au point B. Mais la force de la gravité change cette situation et, après une seconde, le projectile se situe à cinq mètres au-dessous du point B, c'est-à-dire au point C (tout corps qui tombe librement sur la Terre et dans le vide occupe un parcours de cinq mètres dans la première seconde). Donc, si après avoir abaissé ces cinq mètres le projectile était à la même hauteur du point A de la surface terrestre, sa trajectoire serait une courbe concentrique avec la surface de la sphère terrestre.
Maintenant, nous devons calculer la longueur du segment AB, à savoir le chemin horizontal qui occupe le projectile dans la première seconde, de sorte que la vitesse que le projectile doit avoir en sortant de la bouche du canon pour atteindre notre objectif. Le calcul est simple: Prenant le triangle AOB, celui-ci est droit au sommet A. D'autre part, considérant OA = OC = rayon de la sphère terrestre, 6.370.000 m environ, et OB = OC - BC = 6.370.005 m. Nous le disposerons à travers le théorème de Pythagore, environ 8000 m.
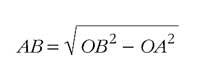
Autrement dit, si l'air n'était pas (cela pose un grand obstacle à tout corps qui va à très grande vitesse), tout projectile lancé horizontalement et à une vitesse initiale de 8 m/s ne tomberait jamais sur Terre.
Et si la vitesse était plus grande, que se passerait-il ? Selon la mécanique de pétrissage. Le projectile de 8 km/s à 11,2 km/s couvrirait les ellipses autour de la Terre et les ellipses seront plus longues à mesure que la vitesse initiale augmente. Mais avec cette vitesse de 11,2 km/s, au lieu d'être ellipse, nous aurons une courbe ouverte, c'est-à-dire une parabole, qui quitte la Terre pour toujours.
Par conséquent, nous pouvons théoriquement lancer une balle de canon jusqu'à la lune. Pour cela, il suffit de lui donner une vitesse initiale élevée.
Maintenant, nous allons analyser le voyage à la Lune en fonction de Jules Verne et de la réalité. Ce qui s'est passé après la lecture de ce roman. Quelque chose d'étonnant s'est produit à ce moment-là : tous les objets qui étaient dans le projectile ont perdu leur poids, et les voyageurs eux-mêmes, qui ont été suspendus dans l'air sans s'accrocher à aucun mur. Mais l'auteur n'a pas tenu compte qu'il devait arriver la même chose avant de passer par ce point et aussi après, c'est-à-dire que des passagers et des objets seraient ingrats dès le début du voyage.
Cela semble une défiguration, mais après avoir réfléchi un peu, nous verrons qu'il doit en être ainsi. Pour réaliser cela, prenons un autre épisode du même roman de Jules Verne. Comme on se souvient du lecteur, les voyageurs ont vu qu'après avoir jeté le corps du chien à l'extérieur, au lieu de tomber celui-ci sur Terre, surpris, ils continuaient dans l'espace avec le projecteur. Vern apporte une réponse adéquate à ce phénomène avec précision et succès. C'est-à-dire, comme nous le savons, comme dans le vide la Terre donne la même accélération à tous les corps, tous tombent à la même vitesse. Dans ce cas, tant le projectile que le corps du chien, en raison de l'influence de la Terre, se déplaceraient exactement la même chose. Par conséquent, la vitesse relative entre eux sera zéro, ou ce qui est la même chose, le corps lancé et les passagers iraient ensemble.
Mais ce que Verne n'a pas pris en compte était: si le corps du chien est hors du projectile et ne tombe pas vers la Terre, pourquoi at-il tomber quand il est à l'intérieur? Si le corps du chien est placé à l'intérieur du projectile (sans aucun support, comme lorsqu'il est à l'extérieur), il est accroché ou reste dans l'espace, à savoir la vitesse relative entre les deux corps est zéro, de sorte qu'il s'arrête l'un de l'autre.

Sans lèvres, tout ce que nous avons dit sur le chien se produit aussi avec les corps, les passagers ou tous les appareils qui sont dans le projectile et donc, même si les points d'appui sont perdus, ne tombent pas. C'est-à-dire, la chaise située sur le trottoir à l'intérieur du projectile qui va en vol, si elle est posée pieds en haut contre le plafond, ne tombera pas en bas et continuera contre le plafond. Tout passager peut s'asseoir dessus sans crainte de tomber au sol du projectile (sinon la chaise tomberait). Mais ce n'est pas possible, parce que nous savons que toutes les choses qui sont dans le projectile ont leur propre accélération.
Apparemment, Jules Verne n'a pas réalisé que, à son avis, à l'intérieur du projectile, en vol libre, les objets pression sur leurs points d'appui, comme ils le font lorsque le projectile est arrêté. Il est vrai que les corps, quand ils sont sur une surface de la zone gravitationnelle, pressent sur elle si le gaizanal se déplace debout ou à une vitesse uniforme, mais quand un corps et son support se déplacent dans l'espace avec la même accélération, aucune pression n'est faite (si les accélérations sont dues à des forces externes, comme c'est le cas, et non à l'influence du moteur du projectile).
Cela signifie qu'une fois l'effet des gaz du canon terminé sur le projectile, les voyageurs et autres objets intérieurs ont perdu leur poids et resteraient sans gravité. Sachant cela, les voyageurs pouvaient facilement le reconnaître dans l'espace libre ou à l'intérieur du canyon. Mais le romancier ne s'en aperçut pas et, dans la première moitié du voyage sidéral, il nous raconte les failles de tête des voyageurs pour savoir s'ils volaient ou non :
- Nicholl, bougeons-nous ?
- Nicholl et Ardan se regardèrent. Ils ne sentaient pas les vibrations du projectile.
- Ou sommes-nous calmes sur le sol de la Floride? Nicholl a demandé.
- Ou au fond du golfe du Mexique, a ajouté Michele.
Ces conditions peuvent être pour les passagers du bateau, mais pas pour les projectiles en vol libre. Les premiers auront leur propre poids, tandis que les seconds perdraient leur gravité et seraient immédiatement pris en compte.
Le voyage de ce type de projectile devrait être surprenant! Un petit monde dans lequel les corps ne pèsent pas et laisseraient les choses libres de la main et continueraient dans un endroit calme sans tomber ; les objets auraient leur équilibre dans n'importe quelle position et l'eau ne tomberait pas quand la bouteille devait doubler...
Malheureusement Jules Verne a pris en compte toutes ces choses qu'il n'avait pas dans son travail "De la Terre à la Lune" et a perdu une grande chance. Cependant, le roman est vraiment merveilleux, malgré une erreur physique.





