De la Tierra a la Luna

Primero, analicemos si teóricamente, al menos, es posible tirar un proyectil con un cañón y no caer éste a la Tierra. La teoría nos dice que sí. Veamos las dos posibilidades extremas. En la primera de ellas, el tiro se realizará verticalmente hacia arriba y con la Tierra sola (ni aire ni cualquier otro tipo de fricción) bastará con dotar al proyectil de la energía cinética necesaria para que salga de la influencia de la Tierra. En el caso de que el cálculo no muy complicado dé al proyectil una velocidad de 12.386 km/s (o superior), se puede observar que ocurrirá lo dicho.
Otra opción es lanzar el proyectil horizontalmente. ¿Por qué en casos normales cae el proyectil a la Tierra? Porque la tierra tira de abajo. Por ello, su recorrido es el de la línea que se inclina hacia el suelo en lugar de ser rectilíneo y finalmente se encuentra con él. Es cierto que la superficie de la Tierra es curva, pero la inclinación de la trayectoria del proyectil es mucho más cerrada que la de la Tierra. Si redujéramos la inclinación de la trayectoria del proyectil y lo hiciéramos tan grande como la superficie de la Tierra, el proyectil nunca caería a la Tierra y seguiría girando alrededor de ella, convirtiéndose en el satélite de la Tierra. ¿Pero cómo se puede conseguir? Como antes, dando al proyectil la velocidad necesaria.
En él tenemos la sección de un sector de la esfera terrestre. El cañón se encuentra en la cima A de un monte. Si la Tierra no tuviera gravedad alguna, después de un segundo de tiro horizontal, el proyectil sería en el punto B. Pero la fuerza de la gravedad cambia esta situación y, tras un segundo, el proyectil se sitúa a cinco metros por debajo del punto B, es decir, en el punto C (cualquier cuerpo que caiga libremente sobre la Tierra y en el vacío ocupa un recorrido de cinco metros en el primer segundo). Por tanto, si después de bajar esos cinco metros el proyectil fuera a la misma altura del punto A de la superficie terrestre, su trayectoria sería una curva concéntrica con la superficie de la esfera terrestre.
Ahora tenemos que calcular la longitud del segmento AB, es decir, el camino horizontal que ocupa el proyectil en el primer segundo, por lo que la velocidad que debe tener el proyectil al salir de la boca del cañón para conseguir nuestro objetivo. El cálculo es sencillo: Tomando el triángulo AOB, éste es recto en el vértice A. Por otra parte, considerando OA = OC = radio de la esfera terrestre, 6.370.000 m aproximadamente, y OB = OC - BC = 6.370.005 m. Lo dispondremos a través del teorema de Pitágoras, unos 8.000 m.
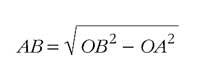
Es decir, si no fuera aire (esto le pone un gran obstáculo a cualquier cuerpo que vaya a velocidad muy alta), cualquier proyectil lanzado horizontalmente y a una velocidad inicial de 8 m/s nunca caería sobre la Tierra.
Y si la velocidad fuera mayor, ¿qué pasaría? Según la mecánica de amasado. El proyectil de 8 km/s a 11,2 km/s cubriría las elipses alrededor de la Tierra y las elipses serán más largas a medida que aumenta la velocidad inicial. Pero con esta velocidad de 11,2 km/s, en lugar de ser elipse, tendremos una curva abierta, es decir, una parábola, que abandona la Tierra para siempre.
Por lo tanto, teóricamente podemos lanzar una bala de cañón hasta la Luna. Para ello sólo hay que darle una alta velocidad inicial.
Ahora vamos a analizar el viaje a la Luna en función de Julio Verne y de la realidad. Lo sucedido tras la lectura de dicha novela. En ese momento sucedió algo sorprendente: todos los objetos que estaban dentro del proyectil perdieron su peso, y los propios viajeros, que se quedaron suspendidos en el aire sin agarrarse a ninguna pared. Pero el autor no tuvo en cuenta que debía suceder lo mismo antes de pasar por este punto y también después, es decir, que tanto pasajeros como objetos estarían ingravemente desde el mismo momento en que comenzó el viaje.
Esto parece una desfiguración, pero después de pensar un poco, veremos que tiene que ser así. Para darse cuenta de esto tomemos otro episodio de la misma novela de Julio Verne. Como se recordará al lector, los viajeros vieron que tras arrojar el cuerpo del perro fuera, en lugar de caer éste a la Tierra, sorprendidos, seguían en el espacio junto con el proyector. Vern da respuesta adecuada a este fenómeno con precisión y acierto. Es decir, como sabemos, como en el vacío la Tierra da la misma aceleración a todos los cuerpos, todos caen a la misma velocidad. En este caso, tanto el proyectil como el cuerpo del perro, debido a la influencia de la Tierra, se desplazarían exactamente igual. Por lo tanto, la velocidad relativa entre ellos será cero, o lo que es lo mismo, el cuerpo lanzado y los pasajeros irían juntos.
Pero lo que Verne no tuvo en cuenta era: si el cuerpo del perro está fuera del proyectil y no cae hacia la Tierra, ¿por qué cae cuando está dentro? Si el cuerpo del perro se coloca en el interior del proyectil (sin ningún tipo de soporte, como cuando está fuera), se cuelga o se queda en el espacio, es decir, la velocidad relativa entre ambos cuerpos es cero, por lo que se detiene uno del otro.

Sin labios, todo lo que hemos dicho sobre el perro ocurre además con los cuerpos, con los pasajeros o con todos los aparatos que están dentro del proyectil y por tanto, aunque se pierdan los puntos de apoyo, no se caen. Es decir, la silla situada sobre el pavimento en el interior del proyectil que va en vuelo, si se colocara patas arriba contra el techo, no se caerá hacia abajo y continuará contra el techo. Cualquier pasajero puede sentarse sobre él sin miedo a caer al suelo del proyectil (de lo contrario la silla caería). Pero eso no es posible, porque sabemos que todas las cosas que están dentro del proyectil tienen su propia aceleración.
Al parecer, Jules Verne no se dio cuenta de que, en su opinión, dentro del proyectil, en vuelo libre, los objetos presionarían en sus puntos de apoyo, como lo hacen cuando el proyectil está parado. Es cierto que los cuerpos, cuando están sobre una superficie de la zona gravitatoria, presionan sobre ella si el gaizanal se está moviendo parado o a una velocidad uniforme, pero cuando un cuerpo y su soporte se mueven en el espacio con la misma aceleración, no se realiza ninguna presión (si las aceleraciones son debidas a fuerzas externas, como es el caso, y no a la influencia del motor del proyectil).
Esto significa que, una vez finalizado el efecto de los gases del cañón en el proyectil, los viajeros y demás objetos interiores perdieron su peso y permanecerían sin gravedad. Sabiendo esto, los viajeros podían reconocerlo fácilmente en el espacio libre o en el interior del cañón. Pero el novelista no se dio cuenta de ello y en la primera mitad del viaje sideral nos cuenta los quebraderos de cabeza que tuvieron los viajeros para saber si volaban o no:
- Nicholl, ¿estamos moviendo?
- Nicholl y Ardan se miraron. No sentían las vibraciones del proyectil.
- ¿O estamos tranquilos sobre el suelo de Florida? Nicholl preguntó.
- O en el fondo del golfo de México, añadió Michele.
Estas condiciones pueden ser para los pasajeros del barco, pero no para los proyectiles en vuelo libre. Los primeros tendrán su peso propio, mientras que los segundos perderían su gravedad y serían inmediatamente a cuenta.
¡El viaje de este tipo de proyectil debería ser sorprendente! Un mundo pequeño en el que los cuerpos no pesan y dejarían las cosas libres de la mano y seguirían en un lugar tranquilo sin caer; los objetos tendrían su equilibrio en cualquier posición y el agua no caería cuando la botella se tuviese que doblar...
Desgraciadamente Julio Verne tuvo en cuenta todas estas cosas que no tenía en su trabajo "De la Tierra a la Luna" y perdió una gran oportunidad. Sin embargo, la novela es realmente maravillosa, a pesar de tener algún error físico.





