Driver history
In short, the control technique needed to drive the robot is long known and can be found in numerous industrial processes.
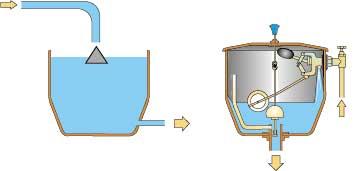
The study of the controllers that have appeared over the years allows to find elements from antiquity. Thus, XVII. Until the 20th century, systems to control the liquid level of an oil lamp or maintain the level of a wine container (even if it fills many glasses) are control systems. In this type of systems the level of the flow control fluid is controlled, since the flow through a hole is proportional to the pressure. The tool that was formerly invented to control the fluid level is a float that is still used in the baths deposits. As the fluid level decreases, the power flow increases and when the level increases, the power flow decreases, eliminating it if necessary. Figure 1 shows the presentation of this tool and the outline of a deposit in the current bathrooms. In this system, the sensor and drive are combined into a single device (float and feed tube).
XVII. and XIX. One of the works that appeared for centuries is the temperature control in the oven designed by Drebbell (1620) and to heat the chicken incubator. Figure 2 presents the design of this control. The furnace consists of a box with internal fire and a pipe with throw regulator. Inside the combustion chamber you can find a chicken incubator with double wall that fills with water the separation between these walls. The temperature sensor is a glass container full of alcohol and mercury located in the mentioned section.
As the fire warms the box and water, the alcohol dilates and the stem carrying the float ascends by lowering the draft regulator to the tube. When the box is too cold, alcohol decreases and the regulator opens and increases the fire force. The desired temperature is given by the length of the stem carrying the float.
At this time, controlling the rotation speed of the axles was an urgent problem of automatic control. For example, controlling the stone speed of a windmill grinding wheat is an automatic control. Among the different methods used, the best was the conical pendulum or based on the ball regulator. This device was used to measure the speed of the mill. But the application that made this type of regulator famous was the steam engine (Watt, 1788). Figure 3 shows the photograph and outline of this machine and Figure 4 shows the foreground of the mobile ball controller.
The action of the centrifugal regulator is easily understandable. Suppose the machine is working in its equilibrium state and suddenly the load is applied to it. At that time the machine speed is reduced and the cone formed by the regulator balls is reduced. Thus, the angle forming the balls with the vertical is used as an output sensor. This action consists of opening the main steam valve (drive) and passing more steam to the machine to recover the lost speed. To maintain the steam valve in this state, the regulator balls must form a different angle, so the speed obtained after the application of the load will not be exactly the same as the previous one.

Watt was a practical engineer, who worked with windmills before, and did not perform a theoretical analysis of the regulator. XIX. At the end of the 20th century, the studies of the aforementioned control system went from being a mere practice to being the nucleus of theoretical analyses. C.V. Airy was a professor of mathematics and astronomy at the University of Cambridge between 1826 and 35 and an astronomer from Greenwich between 1835 and 81. Airy, after numerous studies on speed, discovered that the pendulum regulator could have an unstable motion. Airy is the first analysis of the instability of a control system. The analysis, based on differential equations, was the beginning of the feedback control analysis.
Maxwell’s first systematic work of stability in feedback control was “On Governos” (1868). In this work, Maxwell developed the differential equations of the regulator, lineating them around the equilibrium point. In this way, he showed that stability is associated with the roots of an equation, that is, that these roots should have real negative parts.
The problem of stability criterion, E.J., winner of the 1877 Adams. You can see that it was solved by Routh. The criterion developed in the trial that served to win the prize is the technique that control engineers continue to learn. The analysis of the characteristic equation remained the basis of the control theory in Bell Telephone and H.S. For the inventions of Black, until the appearance of the electronic amplifier fed in 1927.
After the appearance of Routh's work. M. The Russian mathematician Lyapuntov began to study the problem of stability of motion and in 1892 employed nonlinear equations of motion obtaining a result equivalent to Routh's criterion. His work was very important, but it did not appear written until 1958.
XX. If we go into the nineteenth century, the First World War, as well as its importance in the improvement of all techniques, had a great influence the use of control systems, as an example the development of amplifiers fed in 1945 H. W. It is described in an article written by Bode. Electronic amplifiers enabled long-distance calls in the early decades of World War I.
However, as the distance increases, the loss of electrical energy also increases despite the large diameter of the iron thread, and more and more amplifiers are needed to avoid losses. As a result, so many amplifiers distorted due to the lack of linearity of the vacuum tubes used. The solution to this problem was found by Black in feedback: to avoid distortion an increasing feedback is needed. That is, the soft gain of the drive has to grow. Anyone who has tried to increase the volume of a street amplifier would suffer the same situation as Black had suffered, since the absurdity of feedback is destabilized.

Here (in this new technology) was the stability problem mentioned by Maxwell and Routh, but since the dynamics were very complex (equations of order 50), Routh's criterion did not solve much. Communications engineers were accustomed to using both the frequency response and mathematics of complex variables developed by Cauchy, so Bell laboratory analyses focused on a complex field. In 1932 Nyquist published an article on stability.
Stability was analyzed by frequent response charts of the strap. From this theory, a broad method of designing feedback amplifiers was developed.
Together with the feedback amplifier, it began to use the feedback control also in industrial processes. In this field, in complex processes, without linearity and with large delays between the sensor and the actuator, the control, proportional, integral and derivative, referred to by Callender, Hartree and Porter (1936), began to be used.
This technology, based on both experimental work and linearization approaches, developed “tuning” methods to select the appropriate values of the PID controller parameters. At this time, aircraft driving and control devices (of particular relevance, the development of sensors to measure the height and speed of planes) appeared, presenting the control report in this matter in 1973 Mc Ruer.
During World War II there was a great boost to the control of feedback. In the United States, both engineers and mathematicians from the MIT laboratory combined their knowledge to develop Bode's feedback amplifier, PID control of processes, and theories of control of Wiener's stochastic processes (1930). The result was the development of the entire design technique of control mechanisms or serbomechanisms. Many of these works were published and collected in the Radiation Laboratory (James, Michols and Philips, 1947).
In 1948 W.R. developed a new vision in the design of control systems. Evans. This worked with aircraft driving and control systems. Many of the problems that appear present unstable or almost unstable dynamic situations and Evans thought to return to the study of the characteristic equation, that is, to the works of Maxwell and Routh.
Evans developed techniques and rules to graphically follow the geometric layout of the roots of the characteristic equation when modifying a parameter. Its method, the geometric arrangement of the roots, is very suitable for analysis and design of stability and remains an important technique today.
In the 1950s, Bellman and Kalman returned to the United States and Pontryagin Russia to use differential equations as models of control systems. Many of these works appeared as the artificial satellite control area developed. In addition, calculations that could not be performed 10 years earlier were made with digital computers. Lyapuntov's work expanded the study of optimal control initiated by Wiener and Phillips during the war.
These papers were presented at the first conference of the International Federation of Automatic Control held in Moscow in 1960. These control operations were not based on frequency response or characteristic equation, but on differential equations, which resulted in widespread use of computers. These methods are called modern control.
Finally, these new techniques, which appeared from the 1970s onwards, include control in non-linear systems, adaptation control, fuzzy control or multivariate control. The appearance of the computer expanded both the ability to perform complicated calculations and the possibility of using complex algorithms. The development of modern control techniques meant, therefore, a spectacular advance to become increasingly used today.
Therefore, a well-prepared engineer must learn and master many techniques to find the most appropriate answer to a problem. In addition, based on these techniques, you should be able to use and analyze calculations made on the computer.





