Caos no Sistema Solar
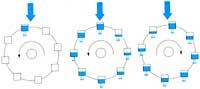
Nas últimas tres décadas os científicos están a realizar grandes esforzos paira aproximarse á explicación do comportamento dos sistemas dinámicos non lineais. A diferenza do que se cre, estes sistemas non sempre evolucionan cara a estados de equilibrio ou de comportamento periódico. Por primeira vez E. Lorenz demostrou en 1963 que os sistemas dinámicos non lineais a miúdo evolucionan de forma totalmente caótica. O sistema de tres ecuacións diferenciais non lineais e tres incógnitas que estudou describe o comportamento da trens denominada roda de auga ou nora de Lorenz. É un bo exemplo paira comprender o tipo de sistema e o comportamento ao que nos referimos. Na figura 1 móstrase o esquema. A auga cae uniformemente pola fonte superior. Os recipientes están perforados e estes tamén perden a auga uniformemente.
Si o caudal da billa é pequeno, o recipiente superior non se encherá e a fricción evitará o movemento. Si o caudal é suficientemente grande, a roda comezará a virar. O instrumento pode alcanzar una velocidade de xiro constante e manterse nese movemento. Si o fluxo da fonte é maior, o xiro será máis rápido e a non linealidad do sistema cobrará maior importancia. Entón, os envases terán menos tempo paira encherse e, doutra banda, baleiraranse moi pouco antes de subir. En consecuencia, os envases que soben poden resultar máis pesados que os que baixan e o xiro investirase.
Segundo descubriu Lorenz, si o aparello abandónase en por si, o xiro pode variar en moitos sentidos, nunca a unha velocidade constante nin a ningunha outra instrución que o converta nun sistema predicible. Este comportamento é tamén o que se atopou no Sistema Solar. Tras evolucionar cíclicamente durante miles ou millóns de anos as peculiaridades da órbita do obxecto, cambian bruscamente o seu comportamento. É inútil coñecer o movemento até entón, xa que a partir dese momento non se poderá prever a evolución. Antes de dar exemplos, hai que mencionar outra característica.

Os científicos, independentemente do ámbito no que traballaban, sempre aceptaron que os pequenos cambios nas condicións iniciais, do mesmo xeito que as pequenas perturbacións que poden producirse ao longo do proceso, producen mínimas modificacións nos resultados. Nos sistemas caóticos non ocorre o mesmo. Ese é o problema que levou a E. Analizar o sistema dinámico non lineal Lorenz. A súa intención inicial era describir adecuadamente a atmosfera paira realizar predicións meteorolóxicas. Paira iso tentouse escribir as ecuacións adecuadas paira unir a variables temperatura, presión e velocidade do vento. Finalmente empezou a traballar cun sistema de doce ecuacións. Por suposto, era un sistema non lineal. Por tanto, inliberable analiticamente. Por iso valeuse da axuda dun primitivo computador da época, utilizando métodos numéricos.
Ao introducir os datos iniciais, deuse conta de que una diferenza moi pequena que consideraba irrelevante provocaba en poucos días un tempo totalmente diferente: este fenómeno chámase dependencia sensible das condicións iniciais. A miúdo tamén se lle coñece como efecto bolboreta. O tempo, pois, non se pode prever do todo a longo prazo. A perturbación provocada polo voo dunha bolboreta tamén pode ser suficiente paira cambiar o tempo dunha rexión en poucos días.
Pode pensarse que estudar o movemento dos compoñentes do Sistema Solar é máis fácil que estudar a evolución da atmosfera. Parece que non se pode comparar a complexidade da atmosfera coa do Sistema Solar, aínda que tamén se teñan en conta os asteroides. Con todo, os problemas teóricos que expón o estudo do Sistema Solar son tamén moi importantes. Aínda que en mecánica pódese liberar facilmente o que se chama problema de dous corpos, o sistema de ecuacións que describe o movemento do sistema formado por tres corpos non pode ser liberado analiticamente. H. Este resultado demostrado por Poincare fai imposible predicir a evolución a longo prazo do sistema. Paira superar esta dificultade, os astrónomos adoitan calcular as súas órbitas utilizando teorías de percusión. Reteñen os temas adecuados ás ecuacións paira ter en conta a influencia de todos os corpos.
A mediados da década do cincuenta, un teorema sobre sistemas dinámicos similares ao Sistema Solar supuxo un avance teórico. Aplicado ao Sistema Solar predí a súa estabilidade cando as masas dos planetas e a excentricidade e inclinación das súas órbitas son pequenas ao longo do tempo.

Con estas bases teóricas e coa inevitable axuda dos primeiros computadores de gran potencia, comezouse a realizar un primeiro estudo significativo sobre a estabilidade do Sistema Solar. Por exemplo, en 1965 a estabilidade dos cinco planetas exteriores predíxose paira os próximos 120.000 anos. Posteriormente o prazo ampliouse a un millón de anos, pero tamén se descubriu que Plutón ten resonancias con Nepturo. Aínda que entón non lles deu importancia, estas interaccións gravitatorias periódicas considéranse na actualidade como a primeira pegada do caos do Sistema Solar. Noutro estudo publicado en 1985, a marxe de estabilidade estendeuse a 5 millóns de anos.
Do mesmo xeito que no caso anterior, apareceron as resonancias de Plutón, pero o período analizado até entón era demasiado curto para que aparecese una conduta caótica. Ao ano seguinte J. Wydow e G. Sussman traballou sobre as órbitas dos mesmos planetas, estudando primeiro a súa aparencia e aparencia nos 107 millóns de anos anteriores e nos 110 millóns de anos futuros, e posteriormente, ampliando o segundo prazo até os 845 millóns de anos. O período de cálculo das particularidades das órbitas era de 32,7 días. Algúns resultados interesantes son os que se mencionan inmediatamente. A inclinación da órbita de Plutón varía entre 14,6º e 16,9º (agora é 17,2º). As resonancias que Neptuno provoca a Plutón fan que este último planeta sufra oscilacións de 3,8, 34, 150 e 600 millóns de anos. Por último, un lixeiro cambio nas condicións iniciais da órbita de Plutón fai que a nova órbita afástese exponencialmente da inicialmente calculada. Os dous últimos resultados son, sobre todo, indicadores do caos.
Máis recentemente o estudo LONGSTOP (Longterm Gravitational Stability Test for Outer Planets) tamén explica nas súas conclusións os fenómenos que poden ser indicadores do Caos. Por exemplo, a pesar de que as variacións que sofren as órbitas son pequenas, son do período membranoso.
Tamén é un estudo sobre os planetas interiores, J en 1989. Presentado por Laskar. Utilizando as ecuacións do movemento de forma analítica simplificada, este científico calculou as órbitas dos planetas interiores en pasos de 500 anos paira os seguintes 200 millóns de anos. Do mesmo xeito que os planetas exteriores, os interiores tamén experimentan pequenas variacións nas súas órbitas, pero a dependencia sensible ás condicións iniciais é evidente. Tamén aparecen as resonancias. Con todo, estas pegadas de caos non deben facer pensar que os planetas nos temos que ver cruzando órbitas e provocando desastres. O problema exponse doutra maneira: aínda que as órbitas dos planetas non cambien demasiado, en ningún caso podemos predicir a posición do planeta a longo prazo.
Até agora falamos da estabilidade da órbita dos planetas, ou o que é o mesmo, da influencia do caos nesas órbitas. De face a toda a estrutura, poderiamos expor outras cuestións, cal será a influencia do caos na configuración do Sistema Solar?. O seu aspecto actual e a súa estabilidade relativa, conseguiunos nos primeiros miles de anos da súa constitución, ou o conseguiu ao longo dos seus case 5.000 millóns de anos?
Hai quen cre que é posible que nunha época haxa outros planetas que logo caían nun comportamento caótico e expulsaríanse, pero, por suposto, é imposible demostralo. Outros creen que a influencia do caos foi limitada, afectando unicamente á dinámica dos asteroides e outros corpos pequenos. Os casos máis concretos e tanxibles de caos deste nivel veranse no seguinte número.
Efemérides de outubroSOL : o 23 de outubro entra en Scorpius ás 3h 57min (UT).
PLANETAS:
|





