Caos en el Sistema Solar
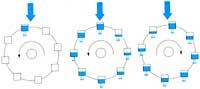
En las últimas tres décadas los científicos están realizando grandes esfuerzos para aproximarse a la explicación del comportamiento de los sistemas dinámicos no lineales. A diferencia de lo que se cree, estos sistemas no siempre evolucionan hacia estados de equilibrio o de comportamiento periódico. Por primera vez E. Lorenz demostró en 1963 que los sistemas dinámicos no lineales a menudo evolucionan de forma totalmente caótica. El sistema de tres ecuaciones diferenciales no lineales y tres incógnitas que estudió describe el comportamiento de la trens denominada rueda de agua o noria de Lorenz. Es un buen ejemplo para comprender el tipo de sistema y el comportamiento al que nos referimos. En la figura 1 se muestra el esquema. El agua cae uniformemente por la fuente superior. Los recipientes están perforados y estos también pierden el agua uniformemente.
Si el caudal del grifo es pequeño, el recipiente superior no se llenará y la fricción evitará el movimiento. Si el caudal es suficientemente grande, la rueda comenzará a girar. El instrumento puede alcanzar una velocidad de giro constante y mantenerse en ese movimiento. Si el flujo de la fuente es mayor, el giro será más rápido y la no linealidad del sistema cobrará mayor importancia. Entonces, los envases tendrán menos tiempo para llenarse y, por otro lado, se vaciarán muy poco antes de subir. En consecuencia, los envases que suben pueden resultar más pesados que los que bajan y el giro se invertirá.
Según descubrió Lorenz, si el aparato se abandona por sí mismo, el giro puede variar en muchos sentidos, nunca a una velocidad constante ni a ninguna otra instrucción que lo convierta en un sistema predecible. Este comportamiento es también el que se ha encontrado en el Sistema Solar. Tras haber evolucionado cíclicamente durante miles o millones de años las peculiaridades de la órbita del objeto, cambian bruscamente su comportamiento. Es inútil conocer el movimiento hasta entonces, ya que a partir de ese momento no se podrá prever la evolución. Antes de dar ejemplos, hay que mencionar otra característica.

Los científicos, independientemente del ámbito en el que trabajaban, siempre han aceptado que los pequeños cambios en las condiciones iniciales, al igual que las pequeñas perturbaciones que pueden producirse a lo largo del proceso, producen mínimas modificaciones en los resultados. En los sistemas caóticos no ocurre lo mismo. Ese es el problema que llevó a E. Analizar el sistema dinámico no lineal Lorenz. Su intención inicial era describir adecuadamente la atmósfera para realizar predicciones meteorológicas. Para ello se intentó escribir las ecuaciones adecuadas para unir las variables temperatura, presión y velocidad del viento. Finalmente empezó a trabajar con un sistema de doce ecuaciones. Por supuesto, era un sistema no lineal. Por lo tanto, inliberable analíticamente. Por ello se valió de la ayuda de un primitivo ordenador de la época, utilizando métodos numéricos.
Al introducir los datos iniciales, se dio cuenta de que una diferencia muy pequeña que consideraba irrelevante provocaba en pocos días un tiempo totalmente diferente: este fenómeno se llama dependencia sensible de las condiciones iniciales. A menudo también se le conoce como efecto mariposa. El tiempo, pues, no se puede prever del todo a largo plazo. La perturbación provocada por el vuelo de una mariposa también puede ser suficiente para cambiar el tiempo de una región en pocos días.
Puede pensarse que estudiar el movimiento de los componentes del Sistema Solar es más fácil que estudiar la evolución de la atmósfera. Parece que no se puede comparar la complejidad de la atmósfera con la del Sistema Solar, aunque también se tengan en cuenta los asteroides. Sin embargo, los problemas teóricos que plantea el estudio del Sistema Solar son también muy importantes. Aunque en mecánica se puede liberar fácilmente lo que se llama problema de dos cuerpos, el sistema de ecuaciones que describe el movimiento del sistema formado por tres cuerpos no puede ser liberado analíticamente. H. Este resultado demostrado por Poincare hace imposible predecir la evolución a largo plazo del sistema. Para superar esta dificultad, los astrónomos suelen calcular sus órbitas utilizando teorías de percusión. Retienen los temas adecuados a las ecuaciones para tener en cuenta la influencia de todos los cuerpos.
A mediados de la década de los cincuenta, un teorema sobre sistemas dinámicos similares al Sistema Solar supuso un avance teórico. Aplicado al Sistema Solar predice su estabilidad cuando las masas de los planetas y la excentricidad e inclinación de sus órbitas son pequeñas a lo largo del tiempo.

Con estas bases teóricas y con la inevitable ayuda de los primeros ordenadores de gran potencia, se comenzó a realizar un primer estudio significativo sobre la estabilidad del Sistema Solar. Por ejemplo, en 1965 la estabilidad de los cinco planetas exteriores se predijo para los próximos 120.000 años. Posteriormente el plazo se amplió a un millón de años, pero también se descubrió que Plutón tiene resonancias con Nepturo. Aunque entonces no les dio importancia, estas interacciones gravitatorias periódicas se consideran en la actualidad como la primera huella del caos del Sistema Solar. En otro estudio publicado en 1985, el margen de estabilidad se extendió a 5 millones de años.
Al igual que en el caso anterior, aparecieron las resonancias de Plutón, pero el periodo analizado hasta entonces era demasiado corto para que apareciera una conducta caótica. Al año siguiente J. Wydow y G. Sussman trabajó sobre las órbitas de los mismos planetas, estudiando primero su apariencia y apariencia en los 107 millones de años anteriores y en los 110 millones de años futuros, y posteriormente, ampliando el segundo plazo hasta los 845 millones de años. El periodo de cálculo de las particularidades de las órbitas era de 32,7 días. Algunos resultados interesantes son los que se mencionan inmediatamente. La inclinación de la órbita de Plutón varía entre 14,6º y 16,9º (ahora es 17,2º). Las resonancias que Neptuno provoca a Plutón hacen que este último planeta sufra oscilaciones de 3,8, 34, 150 y 600 millones de años. Por último, un ligero cambio en las condiciones iniciales de la órbita de Plutón hace que la nueva órbita se aleje exponencialmente de la inicialmente calculada. Los dos últimos resultados son, sobre todo, indicadores del caos.
Más recientemente el estudio LONGSTOP (Longterm Gravitational Stability Test for Outer Planets) también explica en sus conclusiones los fenómenos que pueden ser indicadores del Caos. Por ejemplo, a pesar de que las variaciones que sufren las órbitas son pequeñas, son del período membranoso.
También es un estudio sobre los planetas interiores, J en 1989. Presentado por Laskar. Utilizando las ecuaciones del movimiento de forma analítica simplificada, este científico ha calculado las órbitas de los planetas interiores en pasos de 500 años para los siguientes 200 millones de años. Al igual que los planetas exteriores, los interiores también experimentan pequeñas variaciones en sus órbitas, pero la dependencia sensible a las condiciones iniciales es evidente. También aparecen las resonancias. Sin embargo, estas huellas de caos no deben hacer pensar que los planetas nos tenemos que ver cruzando órbitas y provocando desastres. El problema se plantea de otra manera: aunque las órbitas de los planetas no hayan cambiado demasiado, en ningún caso podemos predecir la posición del planeta a largo plazo.
Hasta ahora hemos hablado de la estabilidad de la órbita de los planetas, o lo que es lo mismo, de la influencia del caos en esas órbitas. De cara a toda la estructura, podríamos plantear otras cuestiones, ¿cuál será la influencia del caos en la configuración del Sistema Solar?. Su aspecto actual y su estabilidad relativa, ¿los consiguió en los primeros miles de años de su constitución, o lo ha conseguido a lo largo de sus casi 5.000 millones de años?
Hay quien cree que es posible que en una época haya otros planetas que luego caían en un comportamiento caótico y se expulsarían, pero, por supuesto, es imposible demostrarlo. Otros creen que la influencia del caos ha sido limitada, afectando únicamente a la dinámica de los asteroides y otros cuerpos pequeños. Los casos más concretos y tangibles de caos de este nivel se verán en el siguiente número.
Efemérides de octubreSOL : el 23 de octubre entra en Scorpius a las 3h 57min (UT).
PLANETAS:
|





