Caos en el Sistema Solar
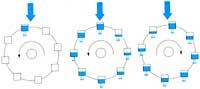
En les últimes tres dècades els científics estan realitzant grans esforços per a aproximar-se a l'explicació del comportament dels sistemes dinàmics no lineals. A diferència del que es creï, aquests sistemes no sempre evolucionen cap a estats d'equilibri o de comportament periòdic. Per primera vegada E. Lorenz va demostrar en 1963 que els sistemes dinàmics no lineals sovint evolucionen de forma totalment caòtica. El sistema de tres equacions diferencials no lineals i tres incògnites que va estudiar descriu el comportament de la trens denominada roda d'aigua o sínia de Lorenz. És un bon exemple per a comprendre el tipus de sistema i el comportament al qual ens referim. En la figura 1 es mostra l'esquema. L'aigua cau uniformement per la font superior. Els recipients estan perforats i aquests també perden l'aigua uniformement.
Si el cabal de l'aixeta és petit, el recipient superior no s'omplirà i la fricció evitarà el moviment. Si el cabal és prou gran, la roda començarà a girar. L'instrument pot aconseguir una velocitat de gir constant i mantenir-se en aquest moviment. Si el flux de la font és major, el gir serà més ràpid i la no linealitat del sistema cobrarà major importància. Llavors, els envasos tindran menys temps per a omplir-se i, d'altra banda, es buidaran molt poc abans de pujar. En conseqüència, els envasos que pugen poden resultar més pesats que els que baixen i el gir s'invertirà.
Segons va descobrir Lorenz, si l'aparell s'abandona per si mateix, el gir pot variar en molts sentits, mai a una velocitat constant ni a cap altra instrucció que el converteixi en un sistema predictible. Aquest comportament és també el que s'ha trobat en el Sistema Solar. Després d'haver evolucionat cíclicament durant milers o milions d'anys les peculiaritats de l'òrbita de l'objecte, canvien bruscament el seu comportament. És inútil conèixer el moviment fins llavors, ja que a partir d'aquest moment no es podrà preveure l'evolució. Abans de donar exemples, cal esmentar una altra característica.

Els científics, independentment de l'àmbit en el qual treballaven, sempre han acceptat que els petits canvis en les condicions inicials, igual que les petites pertorbacions que poden produir-se al llarg del procés, produeixen mínimes modificacions en els resultats. En els sistemes caòtics no ocorre el mateix. Aquest és el problema que va portar a E. Analitzar el sistema dinàmic no lineal Lorenz. La seva intenció inicial era descriure adequadament l'atmosfera per a realitzar prediccions meteorològiques. Per a això es va intentar escriure les equacions adequades per a unir les variables temperatura, pressió i velocitat del vent. Finalment va començar a treballar amb un sistema de dotze equacions. Per descomptat, era un sistema no lineal. Per tant, inliberable analíticament. Per això es va valer de l'ajuda d'un primitiu ordinador de l'època, utilitzant mètodes numèrics.
En introduir les dades inicials, es va adonar que una diferència molt petita que considerava irrellevant provocava en pocs dies un temps totalment diferent: aquest fenomen es diu dependència sensible de les condicions inicials. Sovint també se'l coneix com a efecte papallona. El temps, doncs, no es pot preveure del tot a llarg termini. La pertorbació provocada pel vol d'una papallona també pot ser suficient per a canviar el temps d'una regió en pocs dies.
Pot pensar-se que estudiar el moviment dels components del Sistema Solar és més fàcil que estudiar l'evolució de l'atmosfera. Sembla que no es pot comparar la complexitat de l'atmosfera amb la del Sistema Solar, encara que també es tinguin en compte els asteroides. No obstant això, els problemes teòrics que planteja l'estudi del Sistema Solar són també molt importants. Encara que en mecànica es pot alliberar fàcilment el que es diu problema de dos cossos, el sistema d'equacions que descriu el moviment del sistema format per tres cossos no pot ser alliberat analíticament. H. Aquest resultat demostrat per Poincare fa impossible predir l'evolució a llarg termini del sistema. Per a superar aquesta dificultat, els astrònoms solen calcular les seves òrbites utilitzant teories de percussió. Retenen els temes adequats a les equacions per a tenir en compte la influència de tots els cossos.
A mitjan dècada dels cinquanta, un teorema sobre sistemes dinàmics similars al Sistema Solar va suposar un avanç teòric. Aplicat al Sistema Solar prediu la seva estabilitat quan les masses dels planetes i l'excentricitat i inclinació de les seves òrbites són petites al llarg del temps.

Amb aquestes bases teòriques i amb la inevitable ajuda dels primers ordinadors de gran potència, es va començar a realitzar un primer estudi significatiu sobre l'estabilitat del Sistema Solar. Per exemple, en 1965 l'estabilitat dels cinc planetes exteriors es va predir per als pròxims 120.000 anys. Posteriorment el termini es va ampliar a un milió d'anys, però també es va descobrir que Plutó té ressonàncies amb Nepturo. Encara que llavors no els va donar importància, aquestes interaccions gravitatòries periòdiques es consideren en l'actualitat com la primera petjada del caos del Sistema Solar. En un altre estudi publicat en 1985, el marge d'estabilitat es va estendre a 5 milions d'anys.
Igual que en el cas anterior, van aparèixer les ressonàncies de Plutó, però el període analitzat fins llavors era massa curt perquè aparegués una conducta caòtica. A l'any següent J. Wydow i G. Sussman va treballar sobre les òrbites dels mateixos planetes, estudiant primer la seva aparença i aparença en els 107 milions d'anys anteriors i en els 110 milions d'anys futurs, i posteriorment, ampliant el segon termini fins als 845 milions d'anys. El període de càlcul de les particularitats de les òrbites era de 32,7 dies. Alguns resultats interessants són els que s'esmenten immediatament. La inclinació de l'òrbita de Plutó varia entre 14,6° i 16,9° (ara és 17,2°). Les ressonàncies que Neptú provoca a Plutó fan que aquest últim planeta sofreixi oscil·lacions de 3,8, 34, 150 i 600 milions d'anys. Finalment, un lleuger canvi en les condicions inicials de l'òrbita de Plutó fa que la nova òrbita s'allunyi exponencialment de la inicialment calculada. Els dos últims resultats són, sobretot, indicadors del caos.
Més recentment l'estudi LONGSTOP (Longterm Gravitational Stability Test for Outer Planets) també explica en les seves conclusions els fenòmens que poden ser indicadors del Caos. Per exemple, a pesar que les variacions que sofreixen les òrbites són petites, són del període membranós.
També és un estudi sobre els planetes interiors, J en 1989. Presentat per Laskar. Utilitzant les equacions del moviment de manera analítica simplificada, aquest científic ha calculat les òrbites dels planetes interiors en passos de 500 anys per als següents 200 milions d'anys. Igual que els planetes exteriors, els interiors també experimenten petites variacions en les seves òrbites, però la dependència sensible a les condicions inicials és evident. També apareixen les ressonàncies. No obstant això, aquestes petjades de caos no han de fer pensar que els planetes ens hem de veure creuant òrbites i provocant desastres. El problema es planteja d'una altra manera: encara que les òrbites dels planetes no hagin canviat massa, en cap cas podem predir la posició del planeta a llarg termini.
Fins ara hem parlat de l'estabilitat de l'òrbita dels planetes, o cosa que és el mateix, de la influència del caos en aquestes òrbites. De cara a tota l'estructura, podríem plantejar altres qüestions, quina serà la influència del caos en la configuració del Sistema Solar?. El seu aspecte actual i la seva estabilitat relativa, els va aconseguir en els primers milers d'anys de la seva constitució, o l'ha aconseguit al llarg de les seves gairebé 5.000 milions d'anys?
Hi ha qui creu que és possible que en una època hi hagi altres planetes que després queien en un comportament caòtic i s'expulsarien, però, per descomptat, és impossible demostrar-lo. Uns altres creuen que la influència del caos ha estat limitada, afectant únicament la dinàmica dels asteroides i altres cossos petits. Els casos més concrets i tangibles de caos d'aquest nivell es veuran en el següent número.
Efemèrides d'octubreSOL : el 23 d'octubre entra en Scorpius a les 3h 57min (UT).
PLANETES:
|





