Chaos dans le système solaire
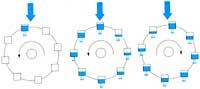
Au cours des trois dernières décennies, les scientifiques font de grands efforts pour se rapprocher de l'explication du comportement des systèmes dynamiques non linéaires. Contrairement à ce qu'on croit, ces systèmes n'évoluent pas toujours vers des états d'équilibre ou de comportement périodique. Pour la première fois, E. Lorenz a démontré en 1963 que les systèmes dynamiques non linéaires évoluent souvent de manière totalement chaotique. Le système de trois équations différentielles non linéaires et trois inconnues qu'il a étudié décrit le comportement de la trens appelée roue d'eau ou roue de Lorenz. C'est un bon exemple pour comprendre le type de système et le comportement que nous entendons. La figure 1 montre le schéma. L'eau tombe uniformément par la source supérieure. Les récipients sont perforés et ils perdent également l'eau uniformément.
Si le débit du robinet est faible, le récipient supérieur ne sera pas rempli et le frottement empêchera le mouvement. Si le débit est suffisamment grand, la roue commencera à tourner. L'instrument peut atteindre une vitesse de rotation constante et rester dans ce mouvement. Si le flux de la source est plus élevé, la rotation sera plus rapide et la non-linéarité du système prendra plus d'importance. Les récipients auront alors moins de temps à remplir et, d'autre part, ils seront vidés très peu avant de monter. Par conséquent, les emballages qui montent peuvent être plus lourds que ceux qui baissent et la rotation sera inversée.
Selon Lorenz, si l'appareil est abandonné par lui-même, la rotation peut varier à bien des égards, jamais à une vitesse constante, ni à aucune autre instruction qui en fait un système prévisible. Ce comportement est également celui qui a été trouvé dans le système solaire. Après avoir développé cycliquement pendant des milliers ou des millions d'années les particularités de l'orbite de l'objet, ils changent brusquement leur comportement. Il est inutile de connaître le mouvement jusqu'alors, car à partir de ce moment on ne pourra pas prévoir l'évolution. Avant de donner des exemples, il faut mentionner une autre caractéristique.

Les scientifiques, indépendamment du domaine dans lequel ils travaillaient, ont toujours accepté que les petits changements dans les conditions initiales, comme les petites perturbations qui peuvent se produire tout au long du processus, produisent des modifications minimes dans les résultats. Dans les systèmes chaotiques, il n'en est pas de même. C'est le problème qui a conduit à E. Analyser le système dynamique non linéaire Lorenz. Son intention initiale était de décrire correctement l'atmosphère pour effectuer des prévisions météorologiques. Pour cela, nous avons essayé d'écrire les équations appropriées pour unir les variables température, pression et vitesse du vent. Il a finalement commencé à travailler avec un système de douze équations. Bien sûr, c'était un système non-linéaire. Par conséquent, inlibérable analytiquement. C'est pourquoi il a utilisé l'aide d'un ordinateur primitif de l'époque, en utilisant des méthodes numériques.
En saisissant les données initiales, il s'est rendu compte qu'une très petite différence qu'il considérait comme insignifiante provoquait en quelques jours un temps totalement différent : ce phénomène s'appelle dépendance sensible aux conditions initiales. Il est souvent aussi connu comme effet papillon. Le temps, donc, ne peut pas être prévu du tout à long terme. La perturbation provoquée par le vol d'un papillon peut également être suffisante pour changer le temps d'une région en quelques jours.
On peut penser qu'étudier le mouvement des composants du système solaire est plus facile que d'étudier l'évolution de l'atmosphère. Il semble qu'on ne peut pas comparer la complexité de l'atmosphère avec celle du Système Solaire, même si les astéroïdes sont également pris en compte. Cependant, les problèmes théoriques posés par l'étude du système solaire sont également très importants. Bien que la mécanique peut facilement libérer ce qui est appelé problème de deux corps, le système d'équations décrivant le mouvement du système formé par trois corps ne peut pas être libéré analytiquement. H. Ce résultat démontré par Poincare rend impossible de prédire l'évolution à long terme du système. Pour surmonter cette difficulté, les astronomes calculent généralement leurs orbites en utilisant des théories de percussion. Ils conservent les bonnes questions aux équations pour tenir compte de l'influence de tous les corps.
Au milieu des années cinquante, un théorème sur des systèmes dynamiques similaires au système solaire a représenté une avancée théorique. Appliqué au système solaire prédit sa stabilité quand les masses des planètes et l'excentricité et l'inclinaison de leurs orbites sont petites au fil du temps.

Avec ces bases théoriques et l'inévitable aide des premiers ordinateurs de grande puissance, une première étude significative sur la stabilité du système solaire a été entreprise. Par exemple, en 1965 la stabilité des cinq planètes extérieures a été prévue pour les 120.000 prochaines années. Le délai a ensuite été étendu à un million d'années, mais il a également été découvert que Pluton a des résonances avec Nepturo. Bien que cela ne leur ait pas donné d'importance, ces interactions gravitationnelles périodiques sont aujourd'hui considérées comme la première empreinte du chaos du système solaire. Dans une autre étude publiée en 1985, la marge de stabilité s'est étendue à 5 millions d'années.
Comme dans le cas précédent, les résonances de Pluton sont apparues, mais la période analysée jusqu'alors était trop courte pour qu'une conduite chaotique apparaisse. L'année suivante J. Wydow et G. Sussman travailla sur les orbites des mêmes planètes, en étudiant d'abord leur apparence et leur apparence dans les 107 millions d'années précédentes et dans les 110 millions d'années à venir, puis en élargissant le deuxième terme jusqu'à 845 millions d'années. La période de calcul des particularités des orbites était de 32,7 jours. Certains résultats intéressants sont ceux qui sont mentionnés immédiatement. L'inclinaison de l'orbite de Pluton varie entre 14,6º et 16,9º (il est maintenant 17,2º). Les résonances que Neptune provoque à Pluton font que cette dernière planète subit des oscillations de 3,8, 34, 150 et 600 millions d'années. Enfin, un léger changement dans les conditions initiales de l'orbite de Pluton fait que la nouvelle orbite s'éloigne exponentiellement de celle initialement calculée. Les deux derniers résultats sont surtout des indicateurs du chaos.
Plus récemment, l'étude LONGSTOP (Longterm Gravitational Stability Test for Outer Planets) explique aussi dans ses conclusions les phénomènes qui peuvent être des indicateurs du Chaos. Par exemple, bien que les variations subies par les orbites soient petites, elles sont de la période membraneuse.
C'est aussi une étude sur les planètes intérieures, J en 1989. Présenté par Laskar. En utilisant les équations du mouvement de manière analytique simplifiée, ce scientifique a calculé les orbites des planètes intérieures en pas de 500 ans pour les 200 millions d'années suivantes. Comme les planètes extérieures, les intérieurs subissent également de petites variations dans leurs orbites, mais la dépendance sensible aux conditions initiales est évidente. Les résonances apparaissent également. Cependant, ces traces de chaos ne doivent pas faire penser que les planètes doivent nous voir traverser des orbites et provoquer des catastrophes. Le problème se pose autrement : même si les orbites des planètes n'ont pas trop changé, nous ne pouvons en aucun cas prédire la position de la planète à long terme.
Jusqu'à présent, nous avons parlé de la stabilité de l'orbite des planètes, ou de l'influence du chaos sur ces orbites. Face à toute la structure, nous pourrions poser d'autres questions, quelle sera l'influence du chaos dans la configuration du système solaire? Leur aspect actuel et leur stabilité relative les ont-ils obtenus au cours des premiers milliers d'années de leur constitution, ou l'ont-ils obtenu au cours de leurs presque 5 milliards d'années ?
Certains croient qu'il est possible qu'à une époque il y ait d'autres planètes qui tombaient alors dans un comportement chaotique et seraient chassées, mais, bien sûr, il est impossible de le démontrer. D'autres croient que l'influence du chaos a été limitée, affectant uniquement la dynamique des astéroïdes et autres petits corps. Les cas les plus concrets et tangibles de chaos de ce niveau se retrouveront dans le prochain numéro.
Éphémérides d'octobreSOL : le 23 octobre il entre à Scorpius à 3h 57min (UT).
PLANÈTES:
|





