Transformada de Fourier
Que hai detrás do caro equipo de científicos? Como procesan os datos que reciben estas máquinas? En xeral, non nos importa moito. Un computador recollerá as medicións e reflectirá os resultados mediante un gráfico moderno. Ademais, canto máis caro sexa o utillaje, máis preciso e mellor.

Desde este punto de vista, queda moito traballo oculto. Como ocorreu este proceso? Aínda que o computador é moi potente, hai que ensinarlle como debe facer o traballo. Para que os datos sexan externalizados, é necesario preparalos paira realizar tratamentos complexos. En case todos os campos da ciencia, este laborioso traballo prepárano os matemáticos e en medicións con datos oscilantes utilízase ademais a transformada de Fourier.
Tremores da Terra
Seguiremos un exemplo do que inventou o matemático Joseph Fourier. Supoñamos que un sismógrafo dixital ponse en marcha nun territorio onde se producen moitos terremotos. Este dispositivo mide constantemente o movemento do chan, rexistrando en cada medida o desprazamento desde o equilibrio, detectando os terremotos mediante vibracións. Tamén se deben medir as menores ondas sísmicas, o que permite coñecer a frecuencia e intensidade da actividade.
Supoñamos que o sismógrafo recibe 5 datos nun segundo, entón haberá que acumular e procesar 432.000 números diarios.
Una sucesión de números non é moi útil. A verdade é que si se representa nun gráfico vese mellor cando se produciron os terremotos e si foron fortes ou non. Con todo, o mellor paira realizar operacións e cálculos é que os números sexan matemáticos. Esta función indica como se modificou a amplitude da onda sísmica co tempo, é dicir, é, en definitiva, un rexistro continuo dos movementos da terra.
Niso consiste precisamente a maior dificultade: como se pode obter una función que se axuste ben a miles de puntos? É certo que una soa fórmula matemática pode representar calquera lista de números recibida? Cando se trata de medicións oscilatorias, obtense mediante a transformación de Fourier. O matemático francés ideou una metodoloxía paira superar facilmente esta gran dificultade.
Curvas de aspecto complexo
O sismólogo pode debuxar os 432.000 puntos obtidos ao longo do día e, simplemente, entrelazando, obterá una curva. Pero se ese día houbo actividade sísmica, esa curva será moi complexa. (Claro, si non hai actividade sísmica todas as medicións serán cero e o traballo do sismólogo non terá sentido). Con todo, cunha curva tan complexa, é moi difícil calcular calquera cousa.
O tratamento de Fourier baséase na descomposición desta complexa curva. Segundo a súa teoría, calquera función pode escribirse como a suma dos seos e os cosenos de distinta frecuencia. Que significa iso? Segundo esta idea, en lugar de calcular a función, pódese utilizar una suma de funcións simples. Na imaxe móstrase un exemplo desta idea:
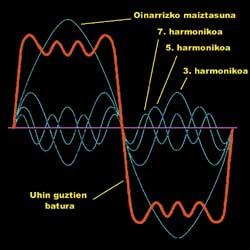
A función complexa (vermella) é a suma de funcións simples (azuis). Na imaxe só hai catro funciones unidas, pero se se utilizan centos, a suma pode axustarse perfectamente aos datos experimentais recolleitos.
Esta metodoloxía facilita os cálculos pero ten outras vantaxes, permite a análise das frecuencias dos datos. Os termos desta suma, esas "funcións simples", son oscilantes, pero cada una delas está relacionada cunha frecuencia. As frecuencias utilizadas en todos os termos son múltiplos dun inicial. Pode dicirse que una función simple representa a contribución dunha determinada frecuencia na función xeral que se desexa buscar. Isto é moi útil paira os científicos.
Por exemplo, o sismólogo pode distinguir dúas ondas sísmicas que se produciron simultaneamente, xa que cada una vibra cunha frecuencia propia. Así mesmo, pode detectar interferencias e desprezar os resultados do ruído de fondo do sismógrafo.
Espazo de frecuencia
A análise de Fourier é igualmente útil en moitos outros ámbitos. O tratamento do son é o exemplo máis claro. Cando o son grávase dixitalmente, o ruído de fondo é orixinado pola propia gravadora. O mero feito de buscar a frecuencia de "limpeza" dese son e de eliminar este termo da función fai que se elimine o ruído do sinal. En óptica, por exemplo, no tratamento fotográfico.
A idea básica é, por tanto, descompor una función complexa en funcións simples sinusoideas. Na linguaxe dos matemáticos, a función debe transformarse do espazo temporal ao espazo de frecuencia. Isto significa que, a partir do tempo de referencia inicial, o conxunto de frecuencias seleccionadas é o mesmo. O procedemento matemático paira realizar este paso é o transformado de Fourier.
Matemático e egiptólogo
Si fixámonos na vida do matemático francés Jean Baptiste Joseph Fourier (1768-1830), XIX. A situación de Europa do século XX reflíctese na intensa actividade profesional que desenvolveu, sobre todo en tres ámbitos. Sempre exerceu una gran actividade en matemáticas, política e arqueoloxía.

A súa fama de matemático é o XIX. desde principios do século. Co obxectivo de estudar a condución de calor en corpos bidimensionales, desenvolveu una metodoloxía con aplicación en case todos os ámbitos da ciencia. Actualmente esta metodoloxía denomínase transformada de Fourier. Pero dedicou moitos anos a desenvolver o transformado: Comezou en 1807 en Grenoble e terminou en París en 1822.
Entrou en política da man da Revolución Francesa. Napoleón participou na expedición a Exipto, onde investigou os restos da antiga civilización e, ao volver a Francia, resumiu o apreso no libro Descrición de Exipto.
O éxito científico da época Fourier levoulle a ser membro da Academia da Ciencia, da Academia Francesa e da Academia de Medicamento.
Aplicacións ...
Comunicacións

Nas comunicacións os sinais son eléctricas, é dicir, simplemente pulsos de tensión. Con todo, estes sinais viaxan a través de amplificadores, filtros e canles de comunicación, podendo alterar estas zonas de moitas maneiras. A transformación de Fourier é imprescindible paira entender como se producen estas transformacións. En definitiva, estes sinais eléctricos xestiónanse en función das frecuencias. No sinal dixital (composta por 0 e 1) tamén é necesario diferenciar as frecuencias. Os pulsos de tensión destes sinais deben axustarse ao ancho de banda das frecuencias, utilizando paira iso a transformada de Fourier.
Sismología
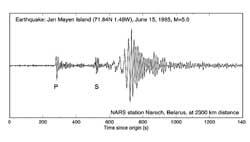
As ondas sísmicas teñen frecuencias propias. A súa análise permite coñecer o tipo e orixe das ondas. Esta análise utilízase constantemente paira investigar terremotos e placas tectónicas, pero non é a única aplicación. Entre outras cousas, na industria do petróleo e o gas utilizouse moito paira buscar novas fontes. Este tipo de investigación utilízase paira diferenciar as ondas sísmicas naturais das provocadas por unha explosión nuclear. Estas separacións dependen das frecuencias, polo que a transformación de Fourier é imprescindible no tratamento matemático dos datos.
Soar

Esta técnica serve paira detectar calquera cousa na auga. O funcionamento básico é moi sinxelo: emítense ondas sonoras cara ao fondo e cando choca contra algo, a onda rebota (eco). A análise da intensidade, frecuencia e tempo de reflexión da onda reflectida permite coñecer a situación e natureza do obxecto. A análise de frecuencias realízase mediante a transformación de Fourier.
Espectroscopia

A espectroscopia utilízase paira identificar os compoñentes químicos dunha sustancia; cando se achega enerxía, cada molécula ten una resposta propia. A molécula "absorbe" ou libera una determinada cantidade de enerxía mediante ondas electromagnéticas. A análise das frecuencias destas ondas permite ao químico identificar as moléculas.
Acústica

O son é una mestura de moitas frecuencias. O timbre dun instrumento, por exemplo, depende das achegas dos armónicos. Por iso, cando o son convértese en sinal eléctrico, a análise de Fourier é imprescindible tanto no tratamento dixital como no analóxico. Por exemplo, a ecualización é actuar con intervalos de frecuencia.
Astronomía

Co radiotelescopio pódense ver cousas que non reflicten luces. Por exemplo, a superficie de Venus está rodeada dunha densa capa de nubes. Pero os astrónomos puideron explorar a súa superficie mediante ondas de radio. É máis, paira calcular o período de rotación hai que ter en conta como se reflicten estas ondas na superficie. Estes estudos requiren unha análise de frecuencias.
Óptica

A transformada de Fourier produce na luz un efecto similar a un prisma: separa os compoñentes que contén, é dicir, os raios de luz de diferente lonxitude de onda. Con todo, isto faise matematicamente, o que significa que os efectos físicos da luz poden ser analizados matematicamente. Por exemplo, ao pasar por unha ranura, pódese coñecer a influencia da difracción na luz. Esta análise aplicada á luz visible serve tamén paira calquera outra lonxitude de onda: microondas, raios X, infravermellos, etc.





