Transformada de Fourier
Què hi ha darrere del car equip de científics? Com processen les dades que reben aquestes màquines? En general, no ens importa molt. Un ordinador recollirà els mesuraments i reflectirà els resultats mitjançant un gràfic modern. A més, com més car sigui l'utillatge, més precís i millor.

Des d'aquest punt de vista, queda molta feina oculta. Com ha ocorregut aquest procés? Encara que l'ordinador és molt potent, cal ensenyar-li com ha de fer el treball. Perquè les dades siguin externalitzades, és necessari preparar-los per a realitzar tractaments complexos. En gairebé tots els camps de la ciència, aquest laboriós treball el preparen els matemàtics i en mesuraments amb dades oscil·lants s'utilitza a més la transformada de Fourier.
Tremolors de la Terra
Seguirem un exemple del que va inventar el matemàtic Joseph Fourier. Suposem que un sismògraf digital es posa en marxa en un territori on es produeixen molts terratrèmols. Aquest dispositiu mesura constantment el moviment del sòl, registrant en cada mesura el desplaçament des de l'equilibri, detectant els terratrèmols mitjançant vibracions. També s'han de mesurar les menors ones sísmiques, la qual cosa permet conèixer la freqüència i intensitat de l'activitat.
Suposem que el sismògraf rep 5 dades en un segon, llavors caldrà acumular i processar 432.000 números diaris.
Una successió de números no és molt útil. La veritat és que si es representa en un gràfic es veu millor quan s'han produït els terratrèmols i si han estat forts o no. No obstant això, el millor per a realitzar operacions i càlculs és que els números siguin matemàtics. Aquesta funció indica com s'ha modificat l'amplitud de l'ona sísmica amb el temps, és a dir, és, en definitiva, un registre continu dels moviments de la terra.
En això consisteix precisament la major dificultat: com es pot obtenir una funció que s'ajusti bé a milers de punts? És cert que una sola fórmula matemàtica pot representar qualsevol llista de números rebuda? Quan es tracta de mesuraments oscil·latoris, s'obté mitjançant la transformació de Fourier. El matemàtic francès va idear una metodologia per a superar fàcilment aquesta gran dificultat.
Corbes d'aspecte complex
El sismòleg pot dibuixar els 432.000 punts obtinguts al llarg del dia i, simplement, entrellaçant, obtindrà una corba. Però si aquest dia hi ha hagut activitat sísmica, aquesta corba serà molt complexa. (Clar, si no hi ha activitat sísmica tots els mesuraments seran zero i el treball del sismòleg no tindrà sentit). No obstant això, amb una corba tan complexa, és molt difícil calcular qualsevol cosa.
El tractament de Fourier es basa en la descomposició d'aquesta complexa corba. Segons la seva teoria, qualsevol funció pot escriure's com la suma dels sins i els cosinus de diferent freqüència. Què significa això? Segons aquesta idea, en lloc de calcular la funció, es pot utilitzar una suma de funcions simples. En la imatge es mostra un exemple d'aquesta idea:
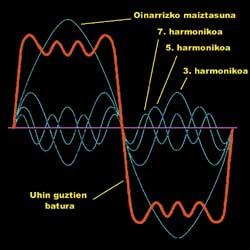
La funció complexa (vermella) és la suma de funcions simples (blaves). En la imatge només hi ha quatre funcions unides, però si s'utilitzen centenars, la suma pot ajustar-se perfectament a les dades experimentals recollits.
Aquesta metodologia facilita els càlculs però té altres avantatges, permet l'anàlisi de les freqüències de les dades. Els termes d'aquesta suma, aquestes "funcions simples", són oscil·lants, però cadascuna d'elles està relacionada amb una freqüència. Les freqüències utilitzades en tots els termes són múltiples d'un inicial. Pot dir-se que una funció simple representa la contribució d'una determinada freqüència en la funció general que es desitja buscar. Això és molt útil per als científics.
Per exemple, el sismòleg pot distingir dues ones sísmiques que s'han produït simultàniament, ja que cadascuna vibra amb una freqüència pròpia. Així mateix, pot detectar interferències i menysprear els resultats del soroll de fons del sismògraf.
Espai de freqüència
L'anàlisi de Fourier és igualment útil en molts altres àmbits. El tractament del so és l'exemple més clar. Quan el so es grava digitalment, el soroll de fons és originat per la pròpia gravadora. El mer fet de buscar la freqüència de neteja "" d'aquest so i d'eliminar aquest terme de la funció fa que s'elimini el soroll del senyal. En òptica, per exemple, en el tractament fotogràfic.
La idea bàsica és, per tant, descompondre una funció complexa en funcions simples sinusoideas. En el llenguatge dels matemàtics, la funció ha de transformar-se de l'espai temporal a l'espai de freqüència. Això significa que, a partir del temps de referència inicial, el conjunt de freqüències seleccionades és el mateix. El procediment matemàtic per a realitzar aquest pas és el transformat de Fourier.
Matemàtic i egiptòleg
Si ens fixem en la vida del matemàtic francès Jean Baptiste Joseph Fourier (1768-1830), XIX. La situació d'Europa del segle XX es reflecteix en la intensa activitat professional que va desenvolupar, sobretot en tres àmbits. Sempre va exercir una gran activitat en matemàtiques, política i arqueologia.

La seva fama de matemàtic és el XIX. des de principis del segle. Amb l'objectiu d'estudiar la conducció de calor en cossos bidimensionals, va desenvolupar una metodologia amb aplicació en gairebé tots els àmbits de la ciència. Actualment aquesta metodologia es denomina transformada de Fourier. Però va dedicar molts anys a desenvolupar el transformat: Va començar en 1807 en Grenoble i va acabar a París en 1822.
Va entrar en política de la mà de la Revolució Francesa. Napoleó va participar en l'expedició a Egipte, on va investigar les restes de l'antiga civilització i, en tornar a França, va resumir l'après en el llibre Descripció d'Egipte.
L'èxit científic de l'època Fourier li va portar a ser membre de l'Acadèmia de la Ciència, de l'Acadèmia Francesa i de l'Acadèmia de Medicina.
Aplicacions ...
Comunicacions

En les comunicacions els senyals són elèctrics, és a dir, simplement polsos de tensió. No obstant això, aquests senyals viatgen a través d'amplificadors, filtres i canals de comunicació, podent alterar aquestes zones de moltes maneres. La transformació de Fourier és imprescindible per a entendre com es produeixen aquestes transformacions. En definitiva, aquests senyals elèctrics es gestionen en funció de les freqüències. En el senyal digital (composta per 0 i 1) també és necessari diferenciar les freqüències. Els polsos de tensió d'aquests senyals han d'ajustar-se a l'amplada de banda de les freqüències, utilitzant per a això la transformada de Fourier.
Sismologia
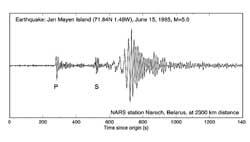
Les ones sísmiques tenen freqüències pròpies. La seva anàlisi permet conèixer el tipus i origen de les ones. Aquesta anàlisi s'utilitza constantment per a investigar terratrèmols i plaques tectòniques, però no és l'única aplicació. Entre altres coses, en la indústria del petroli i el gas s'ha utilitzat molt per a buscar noves fonts. Aquest tipus de recerca s'utilitza per a diferenciar les ones sísmiques naturals de les provocades per una explosió nuclear. Aquestes separacions depenen de les freqüències, per la qual cosa la transformació de Fourier és imprescindible en el tractament matemàtic de les dades.
Sonar

Aquesta tècnica serveix per a detectar qualsevol cosa en l'aigua. El funcionament bàsic és molt senzill: s'emeten ones sonores cap al fons i quan xoca contra alguna cosa, l'ona rebota (eco). L'anàlisi de la intensitat, freqüència i temps de reflexió de l'ona reflectida permet conèixer la situació i naturalesa de l'objecte. L'anàlisi de freqüències es realitza mitjançant la transformació de Fourier.
Espectroscòpia

L'espectroscòpia s'utilitza per a identificar els components químics d'una substància; quan s'aporta energia, cada molècula té una resposta pròpia. La molècula "absorbeix" o allibera una determinada quantitat d'energia mitjançant ones electromagnètiques. L'anàlisi de les freqüències d'aquestes ones permet al químic identificar les molècules.
Acústica

El so és una mescla de moltes freqüències. El timbre d'un instrument, per exemple, depèn de les aportacions dels harmònics. Per això, quan el so es converteix en senyal elèctric, l'anàlisi de Fourier és imprescindible tant en el tractament digital com en l'analògic. Per exemple, l'equalització és actuar amb intervals de freqüència.
Astronomia

Amb el radiotelescopi es poden veure coses que no reflecteixen llums. Per exemple, la superfície de Venus està envoltada d'una densa capa de núvols. Però els astrònoms han pogut explorar la seva superfície mitjançant ones de ràdio. És més, per a calcular el període de rotació cal tenir en compte com es reflecteixen aquestes ones en la superfície. Aquests estudis requereixen una anàlisi de freqüències.
Òptica

La transformada de Fourier produeix en la llum un efecte similar a un prisma: separa els components que conté, és a dir, els raigs de llum de diferent longitud d'ona. Tanmateix, això es fa matemàticament, la qual cosa significa que els efectes físics de la llum poden ser analitzats matemàticament. Per exemple, en passar per una ranura, es pot conèixer la influència de la difracció en la llum. Aquesta anàlisi aplicada a la llum visible serveix també per a qualsevol altra longitud d'ona: microones, raigs X, infrarojos, etc.





